Concours miss sciences mathématique - 2nd S 2017
Première partie (1 point par réponse juste)
Chaque candidate portera sur sa copie, le numéro de la question suivi de la lettre de la réponse choisie.
Aucun point ne sera enlevé pour une réponse fausse ou une absence de réponse
$\begin{array}{|c|c|} \hline \text{Questions }&\text{Réponses proposées }\\ \hline 1. \text{ Soit a et b deux réels tels que }&a. -6<ab<3\\ -2<a\leq\text{ et }-1\leq b<3&b. -6\leq ab\leq1\\ \text{On a :}&c. 2\leq ab\leq 3\\ &d. 2<ab<3\\ \hline 2.\text{ On donne la figure ci-dessous où }&a.{(A\;,1)\ ;\ (B\;,1)\ ;\ (C\;,3)}\\ D\text{ est le milieu de }[AB]\text{ et }&b{(A\;,3)\ ;\ (B\;,3)\ ;\ (C\;,3)}\\ CK=3KD\text{. Le point }K&c{(A\;,3)\ ;\ (B\;,3)\ ;\ (C\;,2)}\\ \text{est le barycentre du système :}&d{(A\;,3)\ ;\ (B\;,3)\ ;\ (C\;,2)}\\ \hline 3. \text{On donne l'inéquation suivantes } &a\left]-\infty\ ;\ -3\right]\cup\left[2\ ;\ +\infty\right[\\ \dfrac{x^{2}-x-6}{x^{2}+1}\geq0&b. \left]-\infty\ ;\ -2\right]\cup\left[3\ ;\ +\infty\right[\\ \text{L’ensemble des solutions, dans}&c\left]-\infty\ ;\ -2\right]\cup\left]-1\ ;\ 1\right[\cup\left[3\ ;\ +\infty\right[\\ \mathbb{R}\text{, de l’inéquation est :}&d\left[-\infty\ ;\ -1\right[\cup\left[1\ ;\ +\infty\right[\\ \hline 4.\text{Soit le tableau de variation }&a. f(a)\text{ et }(b)\text{sont négatifs}\\ \text{ci-dessous d'une fonction }&b. f(a)\text{ est inférieur à }f(b)\\ f\text{définie sur }[-5\ ;\ 5]&c. f(a)\text{ et }f(b)\text{sont de signes contraires }\\ \text{Si }-5<b<a<-1\text{, alors }&d. f(a)\text{est supérieur à }f(b)\\ \hline \begin{array}{|c|rcccccccl|} \hline x&-5&&-1&3&&5\\ \hline &&&2&&&3\\ f(x)&\nearrow&&\searrow&&\nearrow&\\ &-2&&&1&&\\ \hline \end{array}&\\ \hline \end{array}$
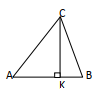
$\begin{array}{|c|c|} \hline 6\text{ On donne la droite }&\\ \left(D_{1}\right)\text{ d’équation cartésienne }&a. \text{ sont confondues}\\2x+2y-5=02text{ et la droite }&\\ \left(D_{2}\right)\text{ d’équations paramétriques : }&b. \text{ sont strictement parallèles }\\ \left\lbrace\begin{array}{rcl}x&=&3t-2\quad\ ;\ t\in\mathbb{R} \\y&=&-2t+3 \end{array}\right.&c. \text{ sont sécantes}\\ \text{Ces deux droites :}&d. \text{ n'ont pas même ordonnée à }\\ &\text{ l'origine }\\ \hline &. \dfrac{2}{1+\cos(x)}\\ 7.\text{ Pour tout réel }x&\\ \text{ appartenant à }\left[0\;,\dfrac{\pi}{2}\right[&b. \dfrac{1}{\cos^{2}(x)}\\ \text{On a :}&c. \dfrac{1}{\cos(x)}\\ \tan(x)+\dfrac{\cos(x)}{1+\sin(x)}.c \dfrac{1}{\cos(x)}\\ \text{est égal à }&d. \dfrac{1}{\sin^{2}(x)}\\ \hline 8.\vec{u}\text{ et }\vec{u}\text{étant deux vecteurs }&a. \dfrac{\pi}{3}\\ \text{non nuls tels que }\left(\vec{u}\;,\vec{v}\right)=\dfrac{\pi}{3}&b. \dfrac{-\pi}{3}\\ \text{La mesure principale de l'angle }&c.\dfrac{2\pi}{3}\\ \left(\vec{u}\;,\vec{v}\right)\text{ est égale à :}&d.\dfrac{-2x}{3}\\ \hline 9.\text{ On considère la figure ci-contre,}&a. 8\\ \text{telle que }BK=2\,cm\;, AB=6\,cm\;, BC=4\,cm\ ;\ &b. -12\\ \text{Le produit scalaire }\overrightarrow{BA}\cdot\overrightarrow{CB}\text{ est égal à :}&c. -8\\ &d. 12\\ \hline 10. \text{Sur la figure ci-dessous, le segment }&a.\dfrac{-3}{2}\\ [\text{ et }]\text{est divisé en partie égales. }&\\ &b.\dfrac{-2}{5}\\ \text{L'homothétie }h\text{ de centre}S&c. \dfrac{3}{5}\\ \text{transformant E en T a pour rapport :}&d.\dfrac{2}{3}\\ \hline \end{array}$
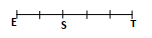
Exercice 1
1. Choisir deux réels strictement positifs, puis comparer le quotient de leur produit par leur somme et le quart de leur somme.
2. Soit $a$ et $b$ deux réels strictement positifs.
a. Démontrer que :
$\dfrac{ab}{a+b}\leq\dfrac{a+b}{4}$
b. Dans quel$(s)$ cas a-t-on l'égalité ?
3. Déduire de la question $2.$ que : si $x>0$, $y>0$ et $z>0$ alors $\dfrac{xy}{x+y}+\dfrac{yz}{y+z}+\dfrac{zx}{z+x}\leq\dfrac{x+y+z}{2}$
Exercice 2
Soit $ABC$ un triangle tel que $AB=3.5\,cm$, $AC=5\,cm$ et $BC=6\,cm$
$M$ et $N$ sont les points définis par : $\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+(K+1)\overrightarrow{AC}$ et $\overrightarrow{AN}=(K+1)\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}$ où $K$ est un réel.
1. Dans cette question, $K=-2.$
a. Faire une figure.
b. Démontrer que les droites $(MN)$ et $(BC)$ sont parallèles.
2. Dans cette question, le réel $k$ est quelconque.
a) Exprimer $\overrightarrow{MN}$ en fonction de $\overrightarrow{BC}$
b. Pour quelle $(s)$ valeur$(s)$ du réel $k$, le quadrilatère $BCMN$ est un parallélogramme ?
c. Pour quelle$(s)$ valeur$(s)$ du réel $k$ a-t-on : $MN=BC$

Ajouter un commentaire