Corrections Exercices Calcul intégral - Tle
Exercice 1
Affirmation 1 :
Une primitive sur ℝ de la fonction définie par :
$f(x) = 3x^2 − 4x + 1$ est la fonction définie par :
$F(x) = x^3 − 2x^2 + x − π$
Solution :
Une primitive de $f(x) = 3x^2 − 4x + 1$ est :
$$
F(x) = \int f(x) \, dx = \int (3x^2 - 4x + 1) \, dx = x^3 - 2x^2 + x + C
$$
Donc, la fonction $F(x) = x^3 − 2x^2 + x − π$ est bien une primitive, car elle correspond à cette forme avec $C = -\pi$.
Réponse : Vrai (V)
Affirmation 2 :
La primitive sur $]0; +∞[$ de la fonction $p(x) = x − \frac{1}{x^2} − \frac{1}{\sqrt{x}}$ qui prend la valeur −½ en 1 est :
$P(x) = \frac{1}{2}x^2 + \frac{1}{x} - 2\sqrt{x} + 1$
Solution :
Cherchons une primitive générale de $p(x)$ :
$$
\int \left(x - \frac{1}{x^2} - \frac{1}{\sqrt{x}}\right) dx = \int x \, dx - \int x^{-2} \, dx - \int x^{-1/2} \, dx
$$
$$
= \frac{1}{2}x^2 + \frac{1}{x} - 2\sqrt{x} + C
$$
Donc la primitive est $P(x) = \frac{1}{2}x^2 + \frac{1}{x} - 2\sqrt{x} + C$. Pour qu'elle prenne la valeur −½ en 1 :
$$
P(1) = \frac{1}{2}(1)^2 + \frac{1}{1} - 2\cdot1 + C = \frac{1}{2} + 1 - 2 + C = -\frac{1}{2} + C
$$
$$
\Rightarrow -\frac{1}{2} + C = -\frac{1}{2} \Rightarrow C = 0
$$
La bonne primitive est donc sans le "+1" à la fin.
X Réponse : Faux (F)
Affirmation 3 :
Une primitive sur un intervalle $I$ de la fonction $u'v + uv'$ est la fonction $u \times v$
Solution :
C'est la règle de dérivation du produit :
$$
(u \cdot v)' = u'v + uv'
\Rightarrow \int (u'v + uv') = uv + C
$$
Réponse : Vrai (V)
| Affirmations | Réponses |
|---|---|
| Une primitive sur ℝ de est | V |
| La primitive de prenant la valeur −½ en 1 est | F |
| Une primitive de est | V |
Exercice 2 : Calcul de primitives
a) $f(x) = \frac{1}{(2x + 5)^2}$ sur $I = \left] \frac{5}{2}; +\infty \right[$
Soit $u(x) = 2x + 5$, donc $u'(x) = 2$
On reconnaît une forme de dérivée d’un quotient :
$$
f(x) = \frac{1}{(2x + 5)^2} = \frac{1}{u(x)^2} = \text{on intègre via } \int \frac{1}{u^2} u'(x) dx
$$
$$
\int \frac{1}{(2x + 5)^2} dx = \int \frac{1}{u^2} \cdot \frac{1}{2} du = -\frac{1}{2u} + C = -\frac{1}{2(2x + 5)} + C
$$
Réponse : $F(x) = -\frac{1}{2(2x + 5)} + C$
b) $f(x) = (3x + 2)(3x^2 + 4x - 7)^3$
Posons $u(x) = 3x^2 + 4x - 7 \Rightarrow u'(x) = 6x + 4 = 2(3x + 2)$
Donc :
$$
f(x) = \frac{1}{2} u'(x) \cdot u(x)^3
\Rightarrow \int f(x) dx = \frac{1}{2} \int u'(x) \cdot u(x)^3 dx = \frac{1}{2} \cdot \frac{u(x)^4}{4} + C
= \frac{(3x^2 + 4x - 7)^4}{8} + C
$$
Réponse : $F(x) = \frac{(3x^2 + 4x - 7)^4}{8} + C$
Exercice 3
$f(x) = x + 1 - e^x$
1) Limites
a) $\lim_{x \to +\infty} f(x) = +\infty + 1 - e^x = -\infty$
b) $\lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x + 1 - e^x}{x} = 1 - \lim_{x \to +\infty} \frac{e^x}{x} = -\infty$
Cela signifie que $f(x)$ décroît très rapidement vers $-\infty$, plus vite que $x$ ne croît.
a) Limite en $-\infty$ :
$$
f(x) = x + 1 - e^x \Rightarrow \lim_{x \to -\infty} x = -\infty, \quad \lim e^x = 0
\Rightarrow \lim_{x \to -\infty} f(x) = -\infty + 1 - 0 = -\infty
$$
b) On cherche si $y = x$ est asymptote.
Soit :
$$
\lim_{x \to -\infty} [f(x) - x] = \lim_{x \to -\infty} (x + 1 - e^x - x) = 1 - e^x \to 1
\Rightarrow f(x) - x \to 1
\Rightarrow \text{asymptote oblique } y = x
$$
c) Étude de $f(x) - x = 1 - e^x$
Si $e^x < 1 \Rightarrow f(x) x$, ce qui se produit pour $x < 0$
Si $e^x 1 \Rightarrow f(x) < x$, ce qui se produit pour $x 0$
Donc :
Sur $]-\infty; 0[$, $f(x) x$
Sur $]0; +\infty[$, $f(x) < x$
2) Tableau de variation de $f$
Calcul de la dérivée :
$$
f'(x) = 1 - e^x
\Rightarrow f'(x) = 0 \Leftrightarrow e^x = 1 \Leftrightarrow x = 0
$$
$f'(x) 0$ pour $x < 0$
$f'(x) < 0$ pour $x 0$
Donc $f$ croît sur $]-\infty, 0[$ puis décroît sur $]0, +\infty[$
Valeur maximale en $x = 0$ : $f(0) = 0 + 1 - 1 = 0$
\begin{array}{|c|c|c|c|}
\hline
x & -\infty & & 0 & &\infty \\
\hline
f'(x) & & + &0 & - & \\
\hline
& & &0 & & \\
f(x) & &\nearrow & &\searrow & \\
&-\infty & & & & -\infty \\
\hline
\end{array}
3) Tracé de $D$ et $C$
Droite $D$ : $y = x$
Courbe $C$ passe par :
$f(0) = 0$
$f(-2) = -2 + 1 - e^{-2} \approx -1 + 0.135 = -0.865$
$f(1) = 1 + 1 - e \approx 2 - 2.718 = -0.718$
Tracer sur repère avec 2 cm/unité.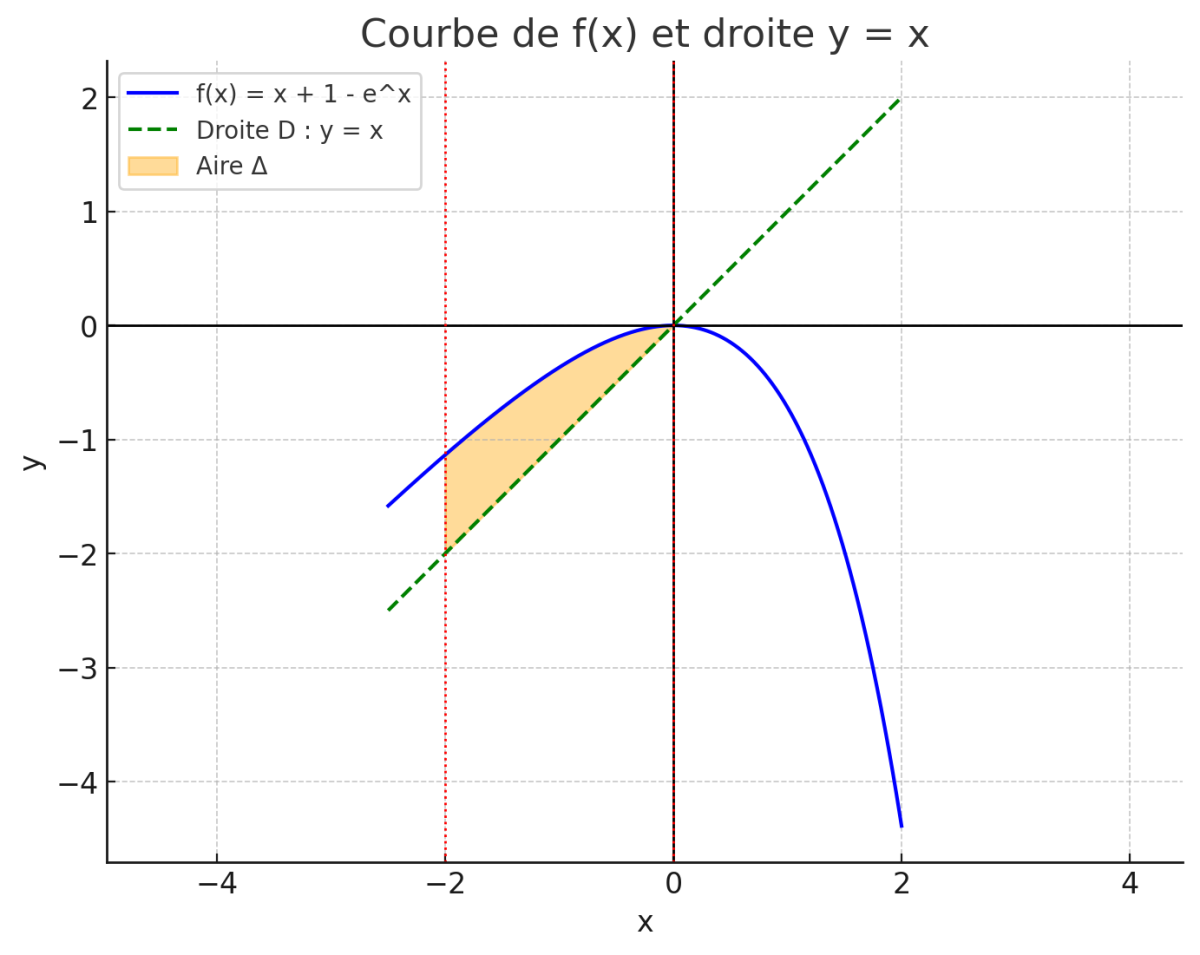
4) Aire $\mathcal{A}$ entre $f$ et $D$, entre $x = -2$ et $x = 0$
On calcule :
$$
\mathcal{A} = \int_{-2}^{0} |f(x) - x| dx = \int_{-2}^{0} (f(x) - x) dx
= \int_{-2}^{0} (x + 1 - e^x - x) dx = \int_{-2}^{0} (1 - e^x) dx
$$
$$
= \left[ x - e^x \right]_{-2}^{0} = \left(0 - 1\right) - \left(-2 - e^{-2}\right) = -1 + 2 + e^{-2} = 1 + e^{-2}
$$
$$
e^{-2} \approx 0.135 \Rightarrow \mathcal{A} \approx 1.135 \, \text{unités d’aire}
$$
Unité graphique : 2 cm → $1 \, \text{u.a.} = 4 \, \text{cm}^2$
$\Rightarrow \mathcal{A} \approx 1.135 \times 4 \approx 4.54 \, \text{cm}^2$
Réponse : environ 4,54 cm²

Ajouter un commentaire