Corrigé BAC MATHÉMATIQUES 2025 S1 : Épreuve du 1er groupe

EXERCICE 1 (4,5 points)

Pour préparer les tests de sélection aux Jeux Olympiques de la Jeunesse de Dakar 2026, les athlètes disposent de deux stades A et B pour les entrainements.

Partie I (2,25 points)

Un athlète doit s’entrainer deux jours consécutifs.

     Le premier jour, la probabilité qu’il choisisse le stade A est égale à $\alpha$.
     Le second jour, on admet que la probabilité qu’il choisisse un stade différent de celui fréquenté la veille est $0,8$.

Pour $j \in \{1, 2\}$, on note les évènements suivants ainsi :

     $A_j$ : « l’athlète choisit le stade A le $j^{\text{ème}}$ jour » ;
     $B_j$ : « l’athlète choisit le stade B le $j^{\text{ème}}$ jour ».

1.Déterminer la valeur de $\alpha$ pour que les évènements $A_1$ et $A_2$ aient la même probabilité.

Dans toute la suite de l’exercice, on prendra $\alpha = 0,5$.

On a :
\[ P(A_1) = \alpha ; P(B_1) = 1 - \alpha ; P(B_2/A_1) = 0,8, P(A_2/A_1) = 0,2 ; P(A_2/B_1) = 0,8 \text{ et } P(B_2/B_1) = 0,2. \]

Or,
\[ P(A_2) = P(A_2 \cap A_1) + P(A_2 \cap B_1) \]
\[ = P(A_2/A_1) \times P(A_1) + P(A_2/B_1) \times P(B_1) \]
\[ = 0,2 \times \alpha + 0,8 \times (1 - \alpha) \]
\[ = -0,6\alpha + 0,8 \]

Ainsi, $P(A_1) = P(A_2) \iff \alpha = -0,6\alpha + 0,8 \iff \alpha = 0,5$.

Autre méthode: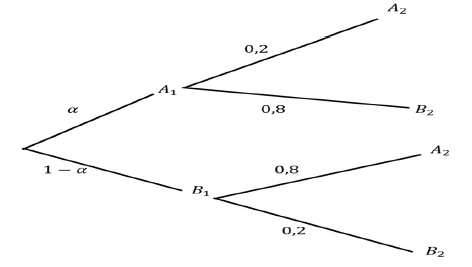

$P(A_2) = 0,2 \times \alpha + 0,8 \times (1-\alpha)= -0,6\alpha + 0,8$

$P(A_2) = -0,6\alpha + 0,8$

Ainsi, $P(A_1) = P(A_2) \Leftrightarrow \alpha = -0,6\alpha + 0,8$

$\Leftrightarrow \alpha = 0,5$

2.Calculer la probabilité qu’un athlète se rende au même stade pendant les deux jours.

Soit $p$ cette probabilité.
\[ p = P(A_1 \cap A_2) + P(B_1 \cap B_2) = 0,1 + 0,1 = 0,2. \]

3.Au deuxième jour, on aperçoit un athlète sortant du stade B. Quelle est la probabilité qu’il se soit entraîné au même stade la veille ?

La probabilité demandée est la probabilité sachant $B_2$ de $B_1$.
\[ p_{B_2}(B_1) = \frac{P(B_1 \cap B_2)}{P(B_2)} = \frac{0,5 \times 0,2}{0,5 \times 0,8 + 0,5 \times 0,2} = 0,2. \]

Partie II (2,25 points)

Au premier jour, on a $n$ athlètes ($n \geq 3$) qui doivent s’entrainer. Chacun d’entre eux choisit, au hasard et indépendamment des choix des autres, l’un des deux stades où il doit s’entrainer.

On suppose que les deux stades ne contiennent aucun athlète au départ.

On dit qu’un athlète est heureux s’il se trouve seul dans un stade.

1.Quelle est la probabilité qu’il y ait deux athlètes heureux ?

Il ne peut pas y avoir deux athlètes heureux car il y a au moins 3 athlètes donc l’un des stades sera occupé par au moins deux athlètes. La probabilité qu’il y ait deux athlètes heureux est nulle.

2.Soit $p_n$ la probabilité qu’il y ait un athlète heureux parmi ces $n$ athlètes.

a) Montrer que pour tout entier naturel $n$ ($n \geq 3$), on a : $p_n = \frac{n}{2^{n-1}}$.

Pour un athlète donné, l’épreuve qui consiste à choisir un stade est une épreuve de Bernoulli dont la probabilité du succès (le stade A) est $0,5$.

Cette épreuve étant effectuée $n$ fois de suite ($n$ athlètes) et de manière indépendante, on a un schéma de Bernoulli.

On a deux cas :

     Un athlète se présente dans le stade A et $n-1$ athlètes sont dans le stade B : 1 succès.
     Un athlète se présente dans le stade B et $n-1$ athlètes sont dans le stade A : $n-1$ succès.

La probabilité qu’il y ait un athlète heureux parmi ces $n$ athlètes est :
\[ p_n = C_n^1(0,5)^1(1 - 0,5)^{n-1} + C_n^{n-1}(0,5)^{n-1}(1 - 0,5)^1 = 2n(0,5)^n = \frac{n}{2^{n-1}}. \]

b) Étudier le sens de variation et la convergence de la suite $(p_n)_{n \geq 3}$.

\[ p_{n+1} - p_n = \frac{n + 1}{2^n} - \frac{n}{2^{n-1}} = \frac{n + 1}{2^n} - \frac{2n}{2^n} = \frac{1 - n}{2^n}. \]

$\forall n \geq 3, p_{n+1} - p_n < 0.$ La suite $(p_n)$ est strictement décroissante.

On a : $p_n = \frac{n}{2^{n-1}} = \frac{2}{\ln 2} \times \frac{\ln 2}{e^{\ln 2}}$. Donc, la suite $(p_n)_{n \geq 3}$ converge vers 0.

c) Calculer $p_{10}$ puis déterminer la plus grande valeur de $n$ pour laquelle la probabilité d’avoir un athlète heureux soit supérieure à $0,005$.

On a : $p_{10} = \frac{5}{256} \approx 0,019 > 0,005$.

La suite $(p_n)$ étant strictement décroissante, on va chercher la plus grande valeur de $n$ supérieure à 10 telle que $p_n$ reste supérieure à $0,005$.

\[ p_{11} = \frac{11}{1024} \approx 0,01 > 0,005 ; p_{12} = \frac{3}{512} \approx 0,0059 > 0,005 ; p_{13} = \frac{13}{4096} \approx 0,0031 < 0,005. \]

La plus grande valeur de $n$ pour laquelle la probabilité d’avoir un athlète heureux soit supérieure à $0,005$ est 12.

EXERCICE 2 (4,25 points)

Soient $(\Delta_1)$ et $(\Delta_2)$ deux droites distinctes de l’espace.

On note $R_1$ et $R_2$ les demi-tours d’axes respectifs $(\Delta_1)$ et $(\Delta_2)$.  

Le but de cet exercice est de déterminer une condition nécessaire et suffisante portant sur $(\Delta_1)$ et $(\Delta_2)$ pour que $R_1 \circ R_2 = R_2 \circ R_1$.

1.On suppose que $(\Delta_1)$ et $(\Delta_2)$ sont perpendiculaires en un point noté $O$.  

On adoptera les notations suivantes :

     Le plan contenant $(\Delta_1)$ et $(\Delta_2)$ est noté $(P)$.
     La droite perpendiculaire en $O$ au plan $(P)$ est notée $(\Delta)$.
     Le plan contenant $(\Delta)$ et $(\Delta_1)$ est noté $(P_1)$.
     Le plan contenant $(\Delta)$ et $(\Delta_2)$ est noté $(P_2)$.
     Les réflexions par rapport aux plans $(P)$, $(P_1)$ et $(P_2)$ sont respectivement notées $S_P$, $S_{P_1}$ et $S_{P_2}$.

a)} Faire une figure en faisant apparaître clairement le point $O$, les plans $(P)$, $(P_1)$ et $(P_2)$ ainsi que les droites $(\Delta)$, $(\Delta_1)$ et $(\Delta_2)$.

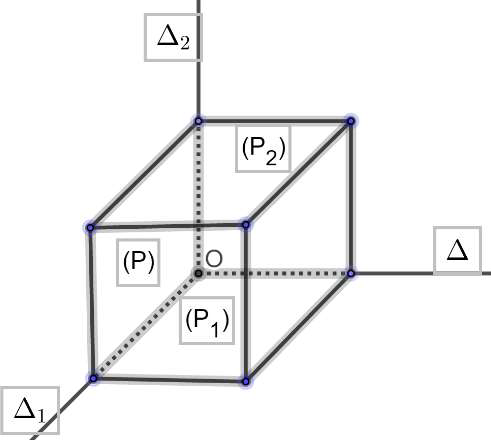
b) Déterminer $S_P \circ S_{P_1}$ et $S_{P_2} \circ S_P$.

     La transformation $S_P \circ S_{P_1}$ est la rotation d’axe $(P) \cap (P_1) = \Delta_1$ et d’angle $2 \times \frac{\pi}{2} = \pi$. C’est donc le \textbf{demi-tour d’axe} $\Delta_1$, c’est-à-dire $R_1$.
     La transformation $S_{P_2} \circ S_P$ est la rotation d’axe $(P) \cap (P_2) = \Delta_2$ et d’angle $2 \times \frac{\pi}{2} = \pi$. C’est donc le \textbf{demi-tour d’axe} $\Delta_2$, c’est-à-dire $R_2$.

c) En déduire que $R_2 \circ R_1$ est un demi-tour dont on précisera l’axe.

\[ R_2 \circ R_1 = (S_{P_2} \circ S_P) \circ (S_P \circ S_{P_1}) = S_{P_2} \circ S_{P_1}. \]

Or, $S_{P_2} \circ S_{P_1}$ est la rotation d’axe $(P_1) \cap (P_2) = \Delta$ et d’angle $2 \times \frac{\pi}{2} = \pi$. C’est donc le \textbf{demi-tour d’axe} $\Delta$.

d) Prouver alors que $R_1 \circ R_2 = R_2 \circ R_1$.

On peut aussi écrire : $R_1 = S_{P_1} \circ S_P$. On a alors :
\[ R_1 \circ R_2 = (S_{P_1} \circ S_P) \circ (S_P \circ S_{P_2}) = S_{P_1} \circ S_{P_2}. \]

Or, $S_{P_1} \circ S_{P_2}$ est aussi la rotation d’axe $(P_1) \cap (P_2) = \Delta$ et d’angle $2 \times \frac{\pi}{2} = \pi$. C’est donc le \textbf{demi-tour d’axe} $\Delta$.

Finalement, $R_1 \circ R_2 = R_2 \circ R_1$.

2.Réciproquement, on suppose que $R_1 \circ R_2 = R_2 \circ R_1$.

Soit $A$ un point de $(\Delta_1)$ qui n’appartient pas à $(\Delta_2)$ et $B$ l’image de $A$ par $R_2$.

a)} Montrer que la droite $(AB)$ et la droite $(\Delta_2)$ sont perpendiculaires.

Soit $(Q)$ le plan passant par $A$ et orthogonal à $(\Delta_2)$ et soit $I$ le point d’intersection de $(Q)$ et $(\Delta_2)$. Dire que le point $B$ est l’image du point $A$ par $R_2$ signifie que $B$ est l’image du point $A$ par la restriction de $R_2$ à $(Q)$ qui est la symétrie centrale de centre $I$. On a $(AB) \subset (Q)$, donc $(\Delta_2)$ est orthogonal à $(AB)$. De plus, $A$, $I$ et $B$ sont alignés. Donc $I \in (\Delta_2) \cap (AB)$. Ainsi, la droite $(AB)$ et la droite $\Delta_2$ sont perpendiculaires en $I$.

b)} En utilisant la relation $R_1 \circ R_2 = R_2 \circ R_1$, prouver que $B = R_1(B)$.

\[ R_1(B) = R_1(R_2(A)) = R_2(R_1(A)) = R_2(A) = B. \]

c)} En déduire que $(\Delta_1)$ et $(\Delta_2)$ sont perpendiculaires.

On a :

     $R_1(B) = B$ ; donc $B \in (\Delta_1)$.
     $A \in \Delta_1$.
     $A \neq B$ car si $A = B$, on aurait $R_2(A) = A$ ; ce qui signifierait que $A \in (\Delta_2)$.

On en déduit que $(AB) = (\Delta_1)$. D’après 2.a), la droite $(AB)$ et la droite $(\Delta_2)$ sont perpendiculaires. On en déduit que $(\Delta_1)$ et $(\Delta_2)$ sont perpendiculaires.

3.En utilisant ce qui précède, énoncer une condition nécessaire et suffisante portant sur $(\Delta_1)$ et $(\Delta_2)$ pour que $R_1 \circ R_2 = R_2 \circ R_1$.

Soient $(\Delta_1)$ et $(\Delta_2)$ deux droites distinctes de l’espace, $R_1$ et $R_2$ les demi-tours d’axes respectifs $(\Delta_1)$ et $(\Delta_2)$.
\[ R_1 \circ R_2 = R_2 \circ R_1 \iff (\Delta_1) \perp (\Delta_2). \]

PROBLÈME (11 points)

On considère le plan complexe $\mathbb{P}$ rapporté à un repère orthonormé direct $(O ; \vec{u}, \vec{v})$.

PARTIE A (2 points)

1.Soit $(a, b) \in \mathbb{R}^* \times \mathbb{R}$ et $F_{a,b}$ l’application de $\mathbb{P}$ dans $\mathbb{P}$ qui au point $M$ d’affixe $z$ fait correspondre le point $M'$ d’affixe $z'$ telle que : $z' = a \overline{z} + ib$ où $\overline{z}$ est le conjugué de $z$.

a) Exprimer les coordonnées $x'$ et $y'$ de $M'$ en fonction des coordonnées $x$ et $y$ de $M$.

\[
\begin{cases}
x' = a x \\
y' = b - a y
\end{cases}
\]

b) Déterminer, suivant les valeurs de $a$ et $b$, l’ensemble des points invariants par $F_{a,b}$.

\[ F_{a,b}(M) = M \Leftrightarrow 
\begin{cases} 
x = a x \\ 
y = b - a y 
\end{cases}
\Leftrightarrow 
\begin{cases} 
x(a - 1) = 0 \\ 
y(1 + a) = b 
\end{cases} \]

     Si $a = 1$ alors $y = \frac{1}{2} b$ et $x$ peut prendre n’importe quelle valeur réelle. L’ensemble des points invariants est la droite d’équation $y = \frac{1}{2} b$.
     Si $a \neq 1$ alors $x = 0$.
    
         Si $a = -1$ et $b \neq 0$, l’ensemble des points invariants est vide.
         Si $a = -1$ et $b = 0$, $y$ peut prendre n’importe quelle valeur réelle. L’ensemble des points invariants est la droite $(D)$ d’équation $x = 0$.
         Si $a \neq -1$, alors $y = \frac{b}{1 + a}$. L’ensemble des points invariants est $\Omega \left( \frac{ib}{1 + a} \right)$.
    

2.On suppose $|a| \neq 1$. Montrer que $F_{a,b} = S_\Delta \circ h$, où $S_\Delta$ est la symétrie orthogonale d’axe la droite $(\Delta)$ d’équation $y = \frac{b}{a + 1}$ et $h$ l’homothétie de centre le point $\Omega$ d’affixe $\frac{ib}{1 + a}$ et de rapport $a$.

Déterminons les expressions analytiques de $S_\Delta$ et de $h$.

Soit $M(x, y)$ et $M'(x', y')$.

Expression analytique de $S_\Delta$} :
\[ S_\Delta(M) = M' \Leftrightarrow 
\begin{cases} 
MM' \text{ est orthogonal à } \vec{u} \\ 
\text{Le milieu } I \text{ de } [MM'] \text{ appartient à } \Delta 
\end{cases} \]
\[
\begin{cases} 
x' = x \\ 
y' = -y + \frac{2b}{1 + a} 
\end{cases} \]

Expression analytique de $h$} :
\[ h(M) = M' \Leftrightarrow \overline{\Omega M'} = a \overline{\Omega M} \]
\[
\begin{cases} 
x' = a x \\ 
y' = a y + \frac{b}{1 + a}(1 - a) 
\end{cases} \]

La composée $S_\Delta \circ h$ a pour expression analytique :
\[
\begin{cases} 
x' = a x \\ 
y' = -\left(a y + \frac{b}{1 + a}(1 - a)\right) + \frac{2b}{1 + a} 
\end{cases} \]
\[ S_\Delta \circ h : 
\begin{cases} 
x' = a x \\ 
y' = -a y + b 
\end{cases} \]

Finalement, $S_\Delta \circ h$ a pour écriture complexe $z' = x' + i y' = a x - a i y + i b = a(x - i y) + i b = a \overline{z} + i b$. Donc $S_\Delta \circ h = F_{a,b}$.

$F_{a,b}$ est la composée de la symétrie orthogonale par rapport à la droite $\Delta$ d’équation $y = \frac{b}{a + 1}$ et de l’homothétie $h$ de centre $\Omega$ d’affixe $Z_\Omega = \frac{i b}{1 + a}$ et de rapport $a$.

3.Soit $(c, d) \in \mathbb{R}^* \times \mathbb{R}$ et $G_{c,d}$ l’application de $\mathbb{P}$ dans $\mathbb{P}$ qui, au point $N$ d’affixe $z$, fait correspondre le point $N'$ d’affixe $z'$ tel que : $z' = c z + i d$.

Déterminer, suivant les valeurs de $c$ et $d$, la nature et les éléments géométriques caractéristiques de $G_{c,d}$.

     Si $c = 1$, $G_{c,d}$ est la translation de vecteur $\vec{v}$ d’affixe $i d$.
     Si $c \neq 1$, $G_{c,d}$ est l’homothétie de centre $\Pi$ d’affixe $\frac{i d}{1 - c}$ et de rapport $c$.

PARTIE B (3,25 points)

1.Dans cette , on suppose que $|a| \neq 1$.

On définit la suite de points $(M_n)_{n \geq 1}$ par :
\[
\begin{cases} 
M_1 \text{ est le point d’affixe } u_1 = a + i b \\ 
\forall n \geq 1, M_{n+1} = F_{a,b}(M_n) 
\end{cases} \]

a)} Déterminer l’affixe $u_2$ du point $M_2$.

\[ M_2 = F_{a,b}(M_1) \Leftrightarrow u_2 = a \overline{u_1} + i b \]
\[ \Leftrightarrow u_2 = a^2 + i b(1 - a) \]

b) Montrer que pour tout entier naturel $n$ non nul, $M_n$ a pour affixe :
\[ u_n = a^n + i b \left( \frac{1 - (-a)^n}{1 + a} \right). \]

On va faire une démonstration par récurrence.

     La formule est vraie pour $n = 1$. En effet, $u_1 = a + i b = a^1 + i b \left( \frac{1 - (-a)^1}{1 + a} \right)$.
     Supposons que la formule est vraie à l’ordre $n$, c’est-à-dire que $M_n$ a pour affixe : $u_n = a^n + i b \left( \frac{1 - (-a)^n}{1 + a} \right)$ et montrons que $M_{n+1}$ a pour affixe : $u_{n+1} = a^{n+1} + i b \left( \frac{1 - (-a)^{n+1}}{1 + a} \right)$.
    \[ M_{n+1} = F_{a,b}(M_n) \Leftrightarrow u_{n+1} = a \overline{u_n} + i b \]
    \[ \Leftrightarrow u_{n+1} = a \left( a^n - i b \left( \frac{1 - (-a)^n}{1 + a} \right) \right) + i b \]
    \[ \Leftrightarrow u_{n+1} = a^{n+1} + i b \left( \frac{1 - (-a)^{n+1}}{1 + a} \right) \]

Conclusion : $M_n$ a pour affixe $u_n = a^n + i b \left( \frac{1 - (-a)^n}{1 + a} \right)$.

c)Soit $(D_1)$ la droite passant par les points $\Omega \left( \frac{i b}{1 + a} \right)$ et $M_1$ et soit $(D_2)$ son image par $F_{a,b}$.

i) Déterminer une équation cartésienne de la droite $(D_2)$.

La droite $(D_1)$ passe par $\Omega \left( 0, \frac{b}{1 + a} \right)$ et $M_1(a + i b)$, donc $(D_1) : y = \frac{b}{1 + a}(x + 1)$.

\[ M'(x', y') \in (D_2) \Leftrightarrow \exists M(x, y) \in (D_1) \text{ tel que } M' = F_{a,b}(M) \]
\[ \Leftrightarrow \exists (x, y) \in \mathbb{R}^2 \text{ tel que } 
\begin{cases} 
y = \frac{b}{1 + a}(x + 1) \\ 
x' = a x \\ 
y' = -a y + b 
\end{cases} \]
\[ \Leftrightarrow \exists (x, y) \in \mathbb{R}^2 \text{ tel que } 
\begin{cases} 
y' = \frac{b}{1 + a}(-x' + 1) \\ 
x' = a x \\ 
y' = -a y + b 
\end{cases} \]

On en déduit que $(D_2)$ a pour équation $y' = \frac{b}{1 + a}(-x' + 1)$ ou, plus simplement :
\[ (D_2) : y = \frac{b}{1 + a}(-x + 1). \]

ii) Montrer que $(D_1)$ est aussi l’image de $(D_2)$ par $F_{a,b}$.

Soit $(D_3)$ l’image de $(D_2)$ par $F_{a,b}$.

\[ M'(x', y') \in (D_3) \Leftrightarrow \exists M(x, y) \in (D_2) \text{ tel que } M' = F_{a,b}(M) \]
\[ \Leftrightarrow \exists (x, y) \in \mathbb{R}^2 \text{ tel que } 
\begin{cases} 
y = \frac{b}{1 + a}(-x + 1) \\ 
x' = a x \\ 
y' = -a y + b 
\end{cases} \]
\[ \Leftrightarrow \exists (x, y) \in \mathbb{R}^2 \text{ tel que } 
\begin{cases} 
y' = \frac{b}{1 + a}(x' + 1) \\ 
x' = a x \\ 
y' = -a y + b 
\end{cases} \]

On en déduit que $(D_3)$ a pour équation $y' = \frac{b}{1 + a}(x' + 1)$ ou, plus simplement :
\[ (D_3) : y = \frac{b}{1 + a}(x + 1). \]

Conclusion : $(D_3) = (D_1)$.

iii) Montrer que, pour tout entier naturel $n$ non nul, le point $M_{2n}$ appartient à $(D_2)$ et le point $M_{2n+1}$ appartient à $(D_1)$.

Soit $n$ un entier naturel non nul.

     Le point $M_{2n}$ a pour affixe $u_{2n} = a^{2n} + i b \left( \frac{1 - (-a)^{2n}}{1 + a} \right)$, c’est-à-dire pour coordonnées $\left( a^{2n}, b \left( \frac{1 - (-a)^{2n}}{1 + a} \right) \right)$. $M_{2n}$ appartient à $(D_2)$ si et seulement si ses coordonnées vérifient l’équation de $(D_2)$.
    \[ \frac{b}{1 + a}(-a^{2n} + 1) = b \left( \frac{1 - a^{2n}}{1 + a} \right) = b \left( \frac{1 - (-a)^{2n}}{1 + a} \right). \]
    D’où $M_{2n}$ appartient à $(D_2)$.
     Le point $M_{2n+1}$ a pour affixe $u_{2n+1} = a^{2n+1} + i b \left( \frac{1 - (-a)^{2n+1}}{1 + a} \right)$, c’est-à-dire pour coordonnées $\left( a^{2n+1}, b \left( \frac{1 - (-a)^{2n+1}}{1 + a} \right) \right)$. $M_{2n+1}$ appartient à $(D_1)$ si et seulement si ses coordonnées vérifient l’équation de $(D_1)$.
    \[ \frac{b}{1 + a}(a^{2n+1} + 1) = b \left( \frac{1 + a^{2n+1}}{1 + a} \right) = b \left( \frac{1 - (-a)^{2n+1}}{1 + a} \right). \]
    D’où $M_{2n+1}$ appartient à $(D_1)$.

2.Dans cette , on suppose que $|c| \neq 1$.

On définit la suite de points $(N_n)_{n \geq 1}$ par :
\[
\begin{cases} 
N_1 \text{ est le point d’affixe } v_1 = c + i d \\ 
\forall n \geq 1, N_{n+1} = G_{c,d}(N_n) 
\end{cases} \]

a) Déterminer l’affixe $v_2$ du point $N_2$.

\[ G_{c,d} : z' = c z + i d \quad G_{c,d} : 
\begin{cases} 
x' = c x \\ 
y' = d + c y 
\end{cases} \]
\[ N_2 = G_{c,d}(N_1) \Leftrightarrow v_2 = c v_1 + i d \]
\[ \Leftrightarrow v_2 = c^2 + i d(1 + c) \]

b) Montrer que pour tout entier naturel $n$ non nul, le point $N_n$ a pour affixe :
\[ v_n = c^n + i d \left( \frac{c^n - 1}{c - 1} \right). \]

     $N_1$ a pour affixe $v_1 = c + i d$, donc vrai au premier rang.
     Supposons que $N_n$ a pour affixe $v_n = c^n + i d \left( \frac{c^n - 1}{c - 1} \right)$.
     Démontrons que $N_{n+1} = G_{c,d}(N_n)$ a pour affixe $v_{n+1} = c^{n+1} + i d \left( \frac{c^{n+1} - 1}{c - 1} \right)$.
    \[ N_{n+1} = G_{c,d}(N_n) \Rightarrow v_{n+1} = c v_n + i d = c \left( c^n + i d \left( \frac{c^n - 1}{c - 1} \right) \right) + i d = c^{n+1} + i d \left( \frac{c^{n+1} - c}{c - 1} \right) + i d = c^{n+1} + i d \left( \frac{c^{n+1} - 1}{c - 1} \right). \]
    Donc vrai au rang $n + 1$.

Conclusion : $N_n$ a pour affixe $v_n = c^n + i d \left( \frac{c^n - 1}{c - 1} \right)$.

c) Montrer que tous les points $N_n$ ($n \in \mathbb{N}^*$) appartiennent à la droite $(\Delta)$ passant par $B$ et $N_1$ où $B$ est le point d’affixe $\frac{i d}{1 - c}$.

\[ B \left( \frac{i d}{1 - c} \right) \text{ et } N_1 (c + i d). \]
\[ (\Delta) : y = \frac{d}{1 - c} (-x + 1). \]
\[ G_{c,d} : 
\begin{cases} 
x' = c x \\ 
y' = d + c y 
\end{cases} \text{ et } v_n = c^n + i d \left( \frac{c^n - 1}{c - 1} \right). \]

On a $\frac{d}{1 - c} (-c^n + 1) = d \left( \frac{c^n - 1}{c - 1} \right) \Rightarrow$ les coordonnées de $N_n$ vérifient l’équation de $(\Delta)$.

PARTIE C (3,25 points)

On considère la famille de courbes $\mathcal{F} = \{C_n, n \geq 1\}$ définie de la manière suivante :

     La courbe $C_1$ est la courbe représentative dans le plan muni du repère orthonormé $(O ; \vec{u}, \vec{v})$ de la fonction $\Phi_1$ définie par : $\Phi_1(x) = x e^{\left( \frac{1}{x} \right)} - 2$.
     Pour tout entier naturel $n \geq 1$, $C_{n+1} = G_{2,1}(C_n)$ où $G_{2,1}$ est l’application de $\mathbb{P}$ dans $\mathbb{P}$ définie dans la 3. de la partie A avec $c = 2$ et $d = 1$.

1.
a) Étudier les variations de $\Phi_1$ puis établir le tableau de variations de $\Phi_1$.

i) Étudions les variations de $\Phi_1$.

$\Phi_1$ est dérivable sur $\mathbb{R}^*$ et $\Phi_1'(x) = \left( 1 - \frac{1}{x} \right) e^{\left( \frac{1}{x} \right)}$.

Sur $]-\infty; 0[ \cup [1; +\infty[$, $\Phi_1' \geq 0$, donc $\Phi_1$ est croissante sur $]-\infty; 0[$ et sur $[1; +\infty[$.

Sur $]0; 1]$, $\Phi_1' \leq 0$, donc $\Phi_1$ est décroissante.

ii) Dressons son tableau de variations.

\[ \lim_{x \to -\infty} \Phi_1(x) = -\infty, \quad \lim_{x \to 0^-} \Phi_1(x) = -2, \quad \lim_{x \to 0^+} \Phi_1(x) = +\infty, \]
\[ \lim_{x \to +\infty} \Phi_1(x) = +\infty. \]

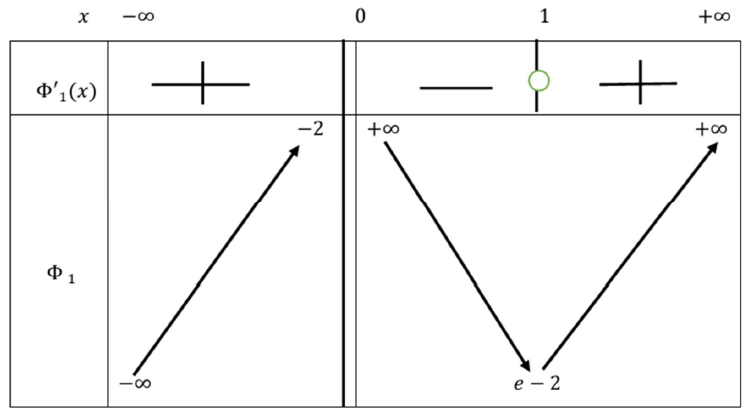
b) Montrer que la droite d’équation \( y = x - 1 \) est asymptote à \( C_1 \).

Soit \( y = x - 1 \), \( \Phi_1(x) - y = x \left( e^{\frac{1}{x}} - 1 \right) - 1 \). En posant \( t = \frac{1}{x} \), on obtient :

\[
\lim_{t \to 0} \frac{e^t - 1}{t} - 1 = 1 - 1 = 0.
\]

Donc la droite \( y = x - 1 \) est asymptote à \( C_1 \) en \( -\infty \) et en \( +\infty \).  
{0,25 pt}

c)Tracer la courbe \( C_1 \):

     \(\lim_{x \to 0^+} \Phi_1(x) = +\infty\), la droite d’équation \( x = 0 \) est une asymptote verticale à \( C_1 \) à droite en 0.
     \(\lim_{x \to 0^-} \Phi'_1(x) = \lim_{x \to 0^-} \left( 1 - \frac{1}{x} \right) e^{\frac{1}{x}} = 0 \) donc \( C_1 \) admet au point de coordonnées (0, -2) une demi-tangente horizontale.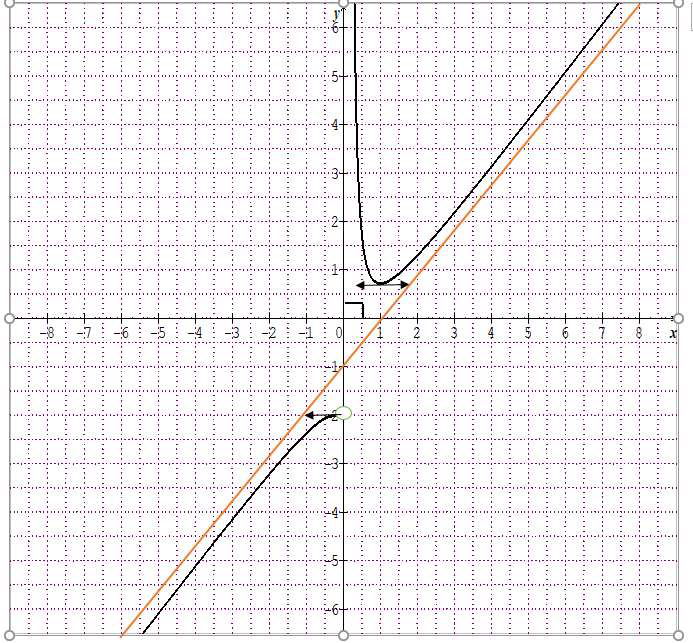

2. Pour tout \( n \in \mathbb{N}^* \), on désigne par \( \Phi_n \) la fonction numérique à variable réelle dont la courbe représentative dans le plan muni du repère orthonormé \( (O; \vec{u}, \vec{v}) \) est \( C_n \).

a)Montrer que \(\forall n \in \mathbb{N}^*\) et \(\forall x \in \mathbb{R}^*\) \(\Phi_n(x) = xe^{\left( \frac{2^n - 1}{x} \right)} - 2^{n-1} - 1\).  

\[
G_{2,1}: z' = 2z + i, \quad G_{2,1} \text{ est l’homothétie de rapport 2 et de centre II d’affixe } - i.
\]

\[
G_{2,1} : \begin{cases} 
x' = 2x \\ 
y' = 1 + 2y 
\end{cases}, \quad C_{n+1} = G_{2,1}(C_n)
\]

Si \(n = 1\), \(\Phi_1 = xe^{\left( \frac{1}{x} \right)} - 2\), donc vrai au premier rang.

Supposons que \(\forall n \in \mathbb{N}^*, \Phi_n(x) = xe^{\left( \frac{2^n - 1}{x} \right)} - 2^{n-1} - 1\).  

Démontrons que \(\forall n \in \mathbb{N}^*, \Phi_{n+1}(x) = xe^{\left( \frac{2^{n+1} - 1}{x} \right)} - 2^n - 1\).  

On a \(\forall n \in \mathbb{N}^*, \Phi_n(x) = xe^{\left( \frac{2^n - 1}{x} \right)} - 2^{n-1} - 1\).  

Or \(C_{n+1} = G_{2,1}(C_n)\) avec \(G_{2,1}\begin{cases} 
x' = 2x \\ 
y' = 1 + 2y 
\end{cases}\).  

\[
y' = 1 + 2\left( \frac{1}{2}x'e^{\left( \frac{2^n - 1}{x} \right)} - 2^{n-1} - 1 \right) = 1 + x'e^{\left( \frac{2^{n+1} - 1}{x} \right)} - 2^n - 2 = x'e^{\frac{2^{n+1} - 1}{x}} - 2^n - 1
\]  

\[
y' = x'e^{\left( \frac{2^{n+1} - 1}{x} \right)} - 2^n - 1, \text{ donc vrai au rang } n + 1.
\]  

Conclusion : \(\forall n \in \mathbb{N}^*, \Phi_n(x) = xe^{\left( \frac{2^n - 1}{x} \right)} - 2^{n-1} - 1\).  
{0,75 pt}

b) Montrer que pour tout entier naturel \(n\) non nul, la droite d’équation \(y = x - 1\) est asymptote à la courbe \(C_n\):  

\[
\Phi_n(x) = xe^{\left( \frac{2^n - 1}{x} \right)} - 2^{n-1} - 1
\]  

\[
\Phi_n(x) - y = x \left( e^{\frac{2^n - 1}{x}} - 1 \right) - 2^{n-1} \text{ en posant } t = \frac{2^{n-1}}{x}
\]  

\[
\lim_{t \to 0} 2^{n-1} \times \frac{e^t - 1}{t} - 2^{n-1} = 2^{n-1} - 2^{n-1} = 0, \text{ par suite toutes les courbes } C_n \text{ ont la même asymptote : la droite d’équation } y = x - 1.
\]  
{0,5 pt}

c)
i)Montrer que pour tout entier naturel \(n\) non nul, il existe un unique point \(S_n\) où la tangente à la courbe \(C_n\) est parallèle à l’axe des abscisses.  

\[
\Phi_n \text{ est dérivable sur } \mathbb{R}^* \text{ et } \forall x \in \mathbb{R}^*, \Phi_n'(x) = \left( 1 - \frac{2^{n-1}}{x} \right) e^{\left( \frac{2^n - 1}{x} \right)}
\]  

\[
\Phi_n'(x) = 0 \Leftrightarrow 1 - \frac{2^{n-1}}{x} = 0 \Leftrightarrow x = 2^{n-1} \text{ et } \Phi_n(2^{n-1}) = 2^{n-1}(e - 1) - 1
\]  

Par conséquent, \(S_n\) a pour coordonnées \((2^{n-1}; 2^{n-1}(e - 1) - 1)\).  

 ii)}Montrer que pour tout entier naturel \(n\) non nul, les points \(S_n, S_{n+1} \text{ et } B(0, -1)\) sont alignés.  

Calculons \( \text{det}(BS_n, BS_{n+1}) \).  

\[
\text{det}(BS_n, BS_{n+1}) = \left| \begin{array}{cc}
2^{n-1} & 2^{n-1}(e - 1) \\
2^n & 2^n(e - 1)
\end{array} \right| = 0 \text{ par suite les points } B, S_n \text{ et } S_{n+1} \text{ sont alignés.}
\]  

Finalement, les points \(S_n\) sont alignés avec \(B(0; -1)\).  
{0,25 pt}

Partie D (2,5 points)

Pour tout entier naturel non nul, on considère la fonction numérique à variable réelle \( h_n \) définie par :  

\[
h_n(x) = x - 1 + 4^{n-1} \left( \frac{e - 2}{x} \right).
\]  

On note \( \mathcal{H}_n \) la courbe représentative de \( h_n \) dans le plan muni du repère orthonormé \( (O ; \vec{u}, \vec{v}) \).

1
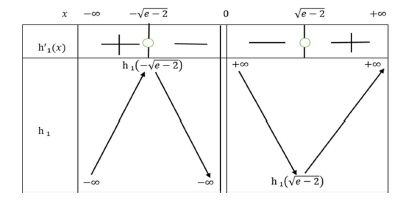
a) Étudier les variations de \( h_1 \) puis dresser son tableau de variations.  

\( h_1 \) est dérivable sur \( \mathbb{R}^* \) et \( \forall x \in \mathbb{R}^* \), \( h'_1(x) = 1 - \frac{e - 2}{x^2} \).  

\( h'_1(x) \geq 0 \) sur \( ]-\infty; -\sqrt{e - 2}[ \cup [\sqrt{e - 2}; +\infty[ \), \( h_1 \) est croissante sur \( ]-\infty; -\sqrt{e - 2}[ \) et sur \( [\sqrt{e - 2}; +\infty[ \).  

\( h'_1(x) \leq 0 \) sur \( [-\sqrt{e - 2}; 0[ \cup ]0; \sqrt{e - 2}] \), \( h_1 \) est décroissante sur \( [-\sqrt{e - 2}; 0[ \) et sur \( ]0; \sqrt{e - 2}] \).  

{0,5 pt}

b)Tracer \( \mathcal{H}_1 \).  {0,5 pt}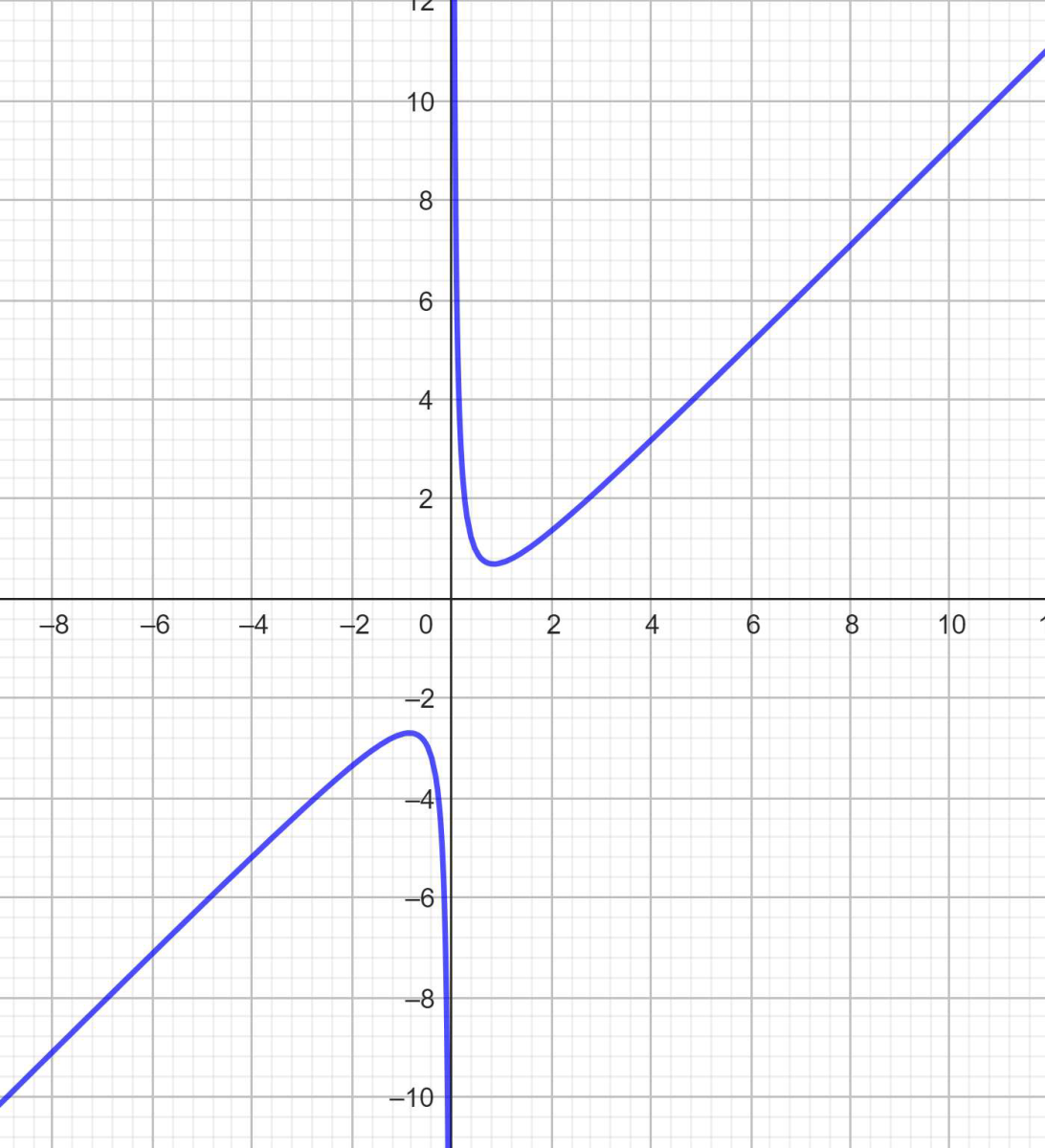

e)Calculer, en unité de volume, le volume du solide obtenu par révolution autour de l’axe des abscisses, de la partie de \( \mathcal{H}_1 \) comprise entre les droites d’équations respectives \( x = 1 \) et \( x = 2 \). Soit \( \mathcal{V} \) ce volume.  

\[
\mathcal{V} = \int_1^2 \pi (h_1(x))^2 \, dx \times \text{uv}
\]  

Or, \((h_1(x))^2 = (x - 1)^2 + 2(e - 2) \left( \frac{x-1}{x} \right) + \left( \frac{e-2}{x} \right)^2\).  

La fonction \( K \) définie par :  

\[
K(x) = \frac{1}{3} (x - 1)^3 + 2(e - 2)(x - \ln x) - \left( \frac{e - 2}{x} \right)
\]  

est une primitive de \((h_1)^2\) sur \([1, 2]\).  

Par conséquent,  

\[
\mathcal{V} = \pi (K(2) - K(1)) \times \text{uv}
\]  

Or, \( K(2) = -\frac{20}{3} + \frac{7e}{2} - 2e\ln 2 + 4\ln 2 \) et \( K(1) = e - 2 \).  

Donc,  

\[
\mathcal{V} = \pi \left( -\frac{14}{3} + \frac{5e}{2} - 2e\ln 2 + \ln 2 \right) \times \text{uv}
\]

2} Montrer que pour tout entier naturel \( n \) non nul, \( H_{n+1} \) est l’image de \( H_n \) par \( G_{2,1} \).  

\( G_{2,1} : z' = 2z + i \), \( G_{2,1} \) est l’homothétie de rapport 2 et de centre \( \Pi \) d’affixe \(-i\).  

\( G_{2,1} : \begin{cases}
x' = 2x \\
y' = 1 + 2y
\end{cases} \)  

On a \( h_n(x) = x - 1 + 4^{n-1} \left( \frac{e - 2}{x} \right) \).  

Cherchons \( G_{2,1}(\text{H}_n) \) avec \( G_{2,1} : \begin{cases}
x' = 2x \\
y' = 1 + 2y
\end{cases} \).  

\[
y' = 1 + 2 \left( \frac{1}{2}x' - 1 + 4^{n-1} \left( \frac{e - 2}{x} \right) \right) = 1 + x' - 2 + 4^n \left( \frac{e - 2}{x} \right),
\]  

\[
y' = x' - 1 + 4^n \left( \frac{e - 2}{x} \right) = h_{n+1}(x).
\]  

Ainsi, \( h_{n+1}(x) = G_{2,1}(\text{H}_n) \).  

{0,5 pt}

3}Pour tout entier naturel \( n \) non nul, on note \( \mathcal{A}_n \) l’aire du domaine plan délimité par les courbes d’équations respectives dans le repère \( (O ; \vec{u}, \vec{v}) : y = h_n(x) , y = x - 1 , x = 2^{n-1} \) et \( x = 2^n \). Montrer que \( (\mathcal{A}_n)_{n \geq 1} \) est une suite géométrique dont on donnera la raison et le premier terme.  

\[
y = h_n(x) , y = x - 1 , x = 2^{n-1} \text{ et } x = 2^n.
\]  

\[
A_n = \int_{2^{n-1}}^{2^n} (h_n(x) - (x - 1)) \, dx = 4^{n-1} (e - 2) \int_{2^{n-1}}^{2^n} \frac{1}{x} \, dx
\]  

\[
A_n = 4^{n-1} (e - 2) [\ln(2^n) - \ln(2^{n-1})] = 4^{n-1} (e - 2) \ln 2
\]  

Pour \( n \in \mathbb{N}^* \), déterminons une relation entre \( A_n \) et \( A_{n+1} \).  

\[
A_n = 4^{n-1} (e - 2) \ln 2 , \quad A_{n+1} = 4^n (e - 2) \ln 2 = 4 A_n
\]  

\[
A_{n+1} = 4 A_n.
\]  

La suite \( (\mathcal{A}_n)_{n \geq 1} \) est une suite géométrique de raison 4 et de premier terme \( \mathcal{A}_1 = (e - 2) \ln 2 \).  

{0,5 pt}