Corrigé Bac Maths S2 1er groupe 2008
Classe:
Terminale
Exercice 1
1) a) On cherche a priori la solution imaginaire pure sous la forme $Z_{0}=\mathrm{i}b\ (b\in\mathbb{R})$, expression qu'on reporte dans l'équation. En écrivant que les parties réelle et imaginaire sont nulles, on obtient le système :
$$\left\lbrace\begin{array}{rcl} -b^{3}+4b^{2}+12b-45&=&0\\ \\6b^{2}-21b+9&=&0\end{array}\right.$$
Après calculs, on trouve $Z_{0}=3\mathrm{i}.$
b) Le premier membre de l'équation s'écrit :
$$P(Z)=(Z-3\mathrm{i})[Z^{2}-(6+\mathrm{i})Z+15+3\mathrm{i}]$$
On trouve : $Z_{1}=3+3\mathrm{i}\ $ et $\ Z_{2}=3-2\mathrm{i}.$
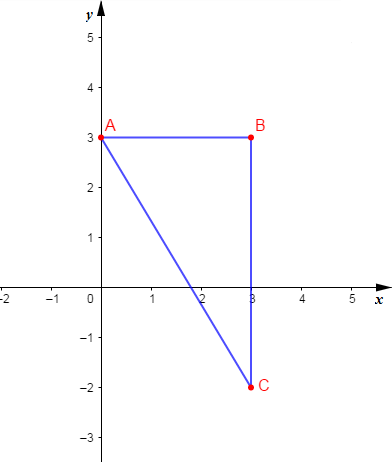
b) $\dfrac{Z_{A}-Z_{B}}{Z_{C}-Z_{B}}=-\dfrac{3}{5}\mathrm{i}\;,\ ABC$ est un triangle rectangle en $B.$
3) a) $f$ est de la forme $Z\longmapsto aZ+b.$
On a : $f(B)=B\ $ et $\ f(A)=C$
D'après a) on a : $Z_{B}-Z_{A}=-\dfrac{3}{5}\mathrm{i}(Z_{B}-Z_{C}).$
Donc, $a=\dfrac{5}{3}\mathrm{i}$
En outre, $\dfrac{b}{1-a}=Z_{B}=3+\mathrm{i}\ \Rightarrow\ b=8-2\mathrm{i}$
Ainsi, $f\ :\ Z\longmapsto\dfrac{5}{3}\mathrm{i}Z+8-2\mathrm{i}$
b) $f$ est la similitude directe de rapport $\dfrac{5}{3}$, d'angle $\dfrac{\pi}{2}\ $ et de centre $B(3\;,\;3)$
Exercice 2
1) a) En dérivant, on trouve :
$$h'=[(b-a)\cos x-(a-b)\sin x]\mathrm{e}^{-x}$$
D'où :
$$h'+h=(b\cos x-a\sin x)\mathrm{e}^{-x}$$
On veut que : $h'+h=\mathrm{e}^{-x}\cos x$, d'où $a=0\ $ et $\ b=1.$
Ainsi,
$$h(x)=\sin x\mathrm{e}^{-x}$$
b) $f$ est solution de $(E)\Rightarrow f'+f=\mathrm{e}^{-x}\cos x$
Or, on a aussi $h'+h=\mathrm{e}^{-x}\cos x$
D'où par différence, $(f-h)'+(f-h)=0 \Rightarrow (f-h)$ est solution de $E_{0}$
Réciproquement, $(f-h)$ est solution de $E_{0}$
$\Rightarrow (f-h)'+(f-h)=0$
$\Rightarrow f'+f=h'+h=\mathrm{e}^{-x}\cos x$
$\Rightarrow f$ est solution de $(E)$
c) Les solutions de $(E_{0})$ sont les fonctions $y$ de la forme $y=K\mathrm{e}^{-x}\;(K\in \mathbb{R}.$
d) Les solutions de $(E)$ sont les fonctions $y$ de la forme $y=K+\sin x$ , car toute solution de $(E)$ est d'après b), la somme de $h$ et d'une solution de $(E_{0}).$
On peut écrire, $y=(K+\sin x)\mathrm{e}^{-x}$
e)
$\begin{array}{rcl} g(0)=0&\Rightarrow&K=0\\&\Rightarrow&y=\sin x\mathrm{e}^{-x}\end{array}$
2) a) $\cos\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}(\cos x-\sin x)$
b) $l'(x)=(\cos x-\sin x)\mathrm{e}^{-x}=\sqrt{2}\cos \left(x+\dfrac{\pi}{4}\right)v^{-x}$
Posons $u=x+\dfrac{\pi}{4}, x\in [0\;,\;2\pi] \Rightarrow u\in \left[\dfrac{\pi}{4}\;;\ \dfrac{9\pi}{4}\right].$
Or dans cet intervalle (faire un schéma du cercle trigonométrique), on a :
$\begin{array}{rcl}\cos u>0&\Leftrightarrow&u\in\left[\dfrac{\pi}{4}\;;\ \dfrac{\pi}{2}\right[\cup\left]\dfrac{3\pi}{2}\;;\ \dfrac{9\pi}{4}\right]\\ \\&\Leftrightarrow&x\in \left[0\;;\ \dfrac{\pi}{4}\right[ \cup \left]\dfrac{5\pi}{4}\;;\ 2\pi\right]\end{array}$
On en déduit le tableau de variation suivant :
$$\begin{array}{|c|lcccccr|}\hline x&0&&\pi/4&&5\pi/4&&2\pi\\ \hline f'(x)&&+&|&-&|&+&\\ \hline&&&\tfrac{\sqrt{2}}{2}\mathrm{e}^{\pi/4}&&&&0\\f&&\nearrow&&\searrow&&\nearrow&\\&0&&&&\tfrac{\sqrt{2}}{2}\mathrm{e}^{5\pi/4}&&\\ \hline\end{array}$$
c) On intègre une première fois par parties en posant :
$u(x)=e^{-x}\Rightarrow u'(x)=-\mathrm{e}^{-x}$
$v'(x)=\sin x\Rightarrow v(x)=-\cos x$
On a alors, $I=\left[-\mathrm{e}^{-x}\cos x\right]_{0}^{2\pi}-\int_{0}^{2\pi}\mathrm{e}^{-x}\cos x\mathrm{d}x$
Désignons par $J$ cette dernière intégrale $(\int_{0}^{2\pi}\mathrm{e}^{-x}\cos xdx)$ et intégrons une seconde fois par parties en posant :
$u(x)=e^{-x}\Rightarrow u'(x)=-\mathrm{e}^{-x}$
$v'(x)=\cos x \Rightarrow v'x)=\sin x$
On a alors $J=\left[e^{-x}\sin x\right]_{0}^{2\pi}+\int_{0}^{2\pi}\mathrm{e}^{-x}\sin x\mathrm{d}x$
On reconnait $I$ dans cette dernière intégrale.
Finalement $I=\left[-\mathrm{e}^{-x}-\mathrm{e}^{-x}\sin x\right]_{0}^{2\pi}-I$
On en déduit que :
$\begin{array}{rcl} 2I&=&\left[-\mathrm{e}^{-x}(\cos x+\sin x)\right]_{0}^{2\pi}\\ \\&=&-\mathrm{e}^{-2\pi}+1\\ \\\Rightarrow\ I&=&\dfrac{1-\mathrm{e}^{-2\pi}}{2}\end{array}$
Exercice 3
A)1) Si la première boule tirée est verte, on la met dans $U_{2}.$
Dans ce cas, $U_{2}$ comporte maintenant $5\;V\ $ et $\ 5\;J.$
On a par conséquent : $p(V_{2}|V_{1})=\dfrac{5}{10}\Rightarrow p(V_{2}|V_{1})=\dfrac{1}{2}$
2) De même $p(V_{2}|R_{1})=\dfrac{1}{11}$
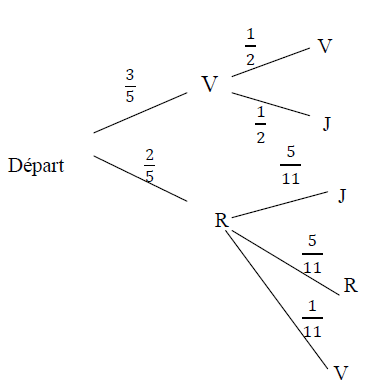
3) Dressons un arbre pondéré de la situation

D'après la formule des probabilités totales, $p(V_{2})=p(V_{2}|V_{1})p(V_{1})+p(V_{2}|R_{1})p(R_{1})$
Soit : $p(V_{2})=\dfrac{1}{2}\times \dfrac{3}{5}+\dfrac{1}{11}\times \dfrac{2}{5}\Rightarrow p(V_{2})=\dfrac{37}{110}$
4) De manière analogue,
$\begin{array}{rcl} p(J_{2})&=&p(J_{2}|V_{1})p(V_{1}+p(J_{2}|R_{1})p(R_{1})\\ \\&=&\dfrac{1}{2}\times\dfrac{3}{5}+\dfrac{1}{11}\times\dfrac{2}{5}\\ \\&=&\dfrac{53}{110}\end{array}$
On trouve $\boxed{p(J_{2})=\dfrac{53}{110}}$
5) De manière analogue à la question 3), on a :
$\begin{array}{rcl} p(R_{2})&=&p(R_{2}|V_{1})p(V_{1}+p(R_{2}|R_{1})p(R_{1}\\ \\&=&0+\dfrac{5}{11}\times\dfrac{2}{5}\\ \\&=&\dfrac{2}{11}\end{array}$
On trouve : $\boxed{p(R_{2})=\dfrac{2}{11}}$
B) 1) La loi de probabilité de $X$ est donnée par le tableau suivant :
$$\begin{array}{|c|c|c|c|}\hline X&1000&500&-500\\ \hline p(X)&\dfrac{37}{110}&\dfrac{53}{110}&\dfrac{2}{11}\\ \hline\end{array}$$
2)
$\begin{array}{rcl} E(X)&=&\sum x_{i}p_{i}\\ \\&=&\left(1000\times \dfrac{37}{110}\right)+\left(500\times \dfrac{53}{110}\right)-\left(500\times \dfrac{2}{11}\right)\\ \\&=&\dfrac{5350}{11}\end{array}$
Donc, $\boxed{E(X)=\dfrac{5350}{11}}$
C) 1) On a affaire à un schéma de Bernoulli, la probabilité du succès étant $p(E)=\dfrac{37}{110}$ et le nombre d'épreuves étant $15.$
La probabilité d'avoir exactement $8$ succès est : $P_{8}=C_{15}^{8}\left(\dfrac{37}{110}\right)^{8}\left(\dfrac{73}{110}\right)^{8}$
2) C'est l'événement : $SSSSSSSS EEEEEEE$ $(8$ succès consécutifs suivis de $7$ échecs consécutifs).
Sa probabilité est :
$\begin{array}{rcl} p(S)^{8}\times p(E)^{7}&=&\left(\dfrac{37}{110}\right)^{8}\left(\dfrac{73}{110}\right)^{8}\\ \\&\simeq&9.3 10^{-6}\end{array}$
3) l'événement contraire est : $P_{0}=C_{15}^{0}\left(\dfrac{37}{110}\right)^{0}\left(\dfrac{73}{110}\right)^{15}$
La probabilité cherchée est donc :
$\begin{array}{rcl} p&=&1-p_{0}\\ \\&=&1-\left(\dfrac{73}{110}\right)^{15}\\ \\&\simeq&0.997\end{array}$
Exercice 4
1)

2) $G$ a pour coordonnées $(\bar{x}\;,\ \bar{y})$ avec :
$$\bar{x}=\dfrac{1}{N}\sum x_{i}\simeq 5.28\quad\text{et}\quad\bar{y}=\dfrac{1}{N}\sum y_{i}\simeq 17.28$$
3) a) $\sigma_{xy}=\dfrac{1}{N}\sum x_{i}y_{i}-\bar{x}\times\bar{y}\simeq 50.63$
$$\sigma_{x}=\sqrt{\dfrac{1}{N}\sum x_{i}^{2}-\bar{x}^{2}}\simeq 4.66\quad\text{et}\quad\sigma_{y}=\sqrt{\dfrac{1}{N}\sum y_{i}^{2}-\bar{y}^{2}}\simeq 11.39$$
Le coefficient de corrélation linéaire est donné par la formule :
$$r=\dfrac{\sigma_{xy}}{\sigma_{x}\times\sigma_{y}}\simeq 0.99$$
b) $r$ est très proche de $1$, donc on a une très bonne corrélation.
4) $D_{y/x}$ a pour équation :
$$y-\bar{y}=a(x-\bar{x})$$
avec $a=\dfrac{\sigma_{xy}}{\sigma_{x}^{2}}$
Après calculs, on trouve qu'une équation de $D_{y/x}$ est :
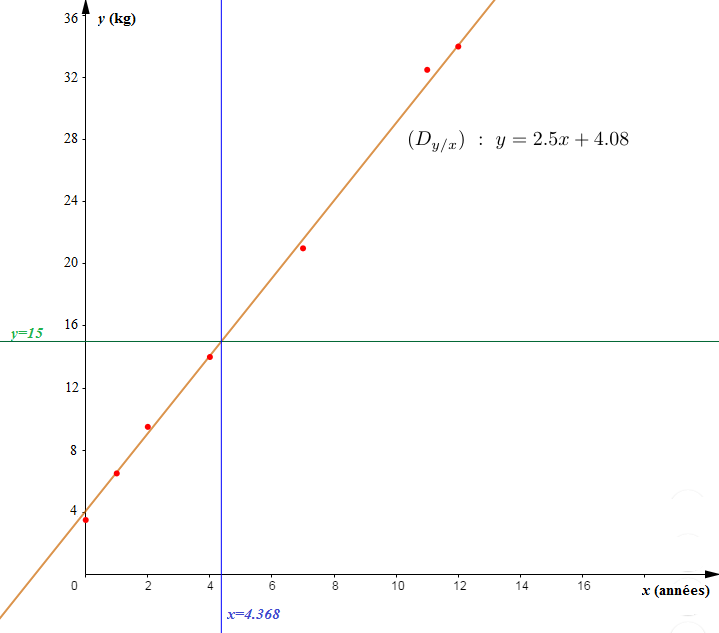
$$y=2.5x+4.08$$
5) a) D'après le graphique, on constate que les valeurs de $y$ supérieures à $15$ correspondent aux valeurs de $x$ supérieures à $4.368.$
On ainsi dire qu'à partir de $5$ ans le poids de l'enfant sera supérieur à $15\;kg.$
b) Pour retrouver ce résultat par le calcul, on considère l'équation $D_{y/x}$ de la droite de régression de $y$ en $x.$
Soit $(D_{y/x})\ :\ y=2.5x+4.08$ alors, on a :
$\begin{array}{rcrcl} y>15&\Leftrightarrow&2.5x+4.08&>&15\\ \\&\Leftrightarrow&2.5x&>&15-4.08\\ \\&\Leftrightarrow&x&>&\dfrac{10.92}{2.5}\\ \\&\Leftrightarrow&x&>&4.368\end{array}$
D'où, $y>15\ \Leftrightarrow\ x>4.368$

Ajouter un commentaire