Corrigé Bac Maths S2-S2A-S4-S5 1er groupe 2013
Classe:
Terminale
Exercice 1
1) a) Soit : $r=\dfrac{cov(X\;,\ Y)}{\sigma_{X}\sigma_{Y}}$
Donc, $r=-0.973$
Ce qui signifie qu'il y a une forte corrélation.
b) La droite de régression de $Y$ en $X$ est :
$\begin{array}{rcl} y&=&ax+b\quad\text{avec }a=\dfrac{cov(X\;,\ Y)}{V(X)}\ \text{ et }\ b=\overline{Y}-a\overline{X}\\ \\&=&-0.874x+4.12\end{array}$
Ainsi, $\boxed{y=-0.874x+4.12}$
c) Si $x=6$ alors, $y=-1.124$
Cette équation ne permet pas d'estimer le degré de salinité car au $6^{\text{ième}}$ mois de pluie le degré de salinité ne peut être négatif.
2) $Z=\ln(Y-1)$
a) Le tableau correspondant à la série $(X\;,\ Z)$ est donné par :
$$\begin{array}{|c|c|c|c|c|c|}\hline X_{i}&0&1&2&3&4\\ \hline Z_{i}&1.182&0.875&0.010&-1.830&-4.610\\ \hline\end{array}$$
b) Le coefficient de corrélation linéaire de cette série $(X\;,\ Z)$ est :
$$r=\dfrac{cov(X\;,\ Z)}{\sigma_{X}\sigma_{Z}}=-0.944$$
La droite de régression de $Z$ en $X$ est :
$\begin{array}{rcl} z&=&ax+b\quad\text{avec }a=\dfrac{cov(X\;,\ Z)}{V(X)}\ \text{ et }\ b=\overline{Z}-a\overline{X}\\ \\&=&-1.428x+1.982\end{array}$
D'où, $\boxed{z=-1.428x+1.982}$
Exprimons $Y$ en fonction de $X$
On a : $z=\ln(y-1)\ $ et $\ z=-1.428x+1.982$ d'où,
$\begin{array}{rcrcl} \ln(y-1)=-1.428x+1.982&\Rightarrow&y-1&=&\mathrm{e}^{-1.428x+1.982}\\ \\&\Rightarrow&y&=&\mathrm{e}^{-1.428x+1.982}+1\end{array}$
Ainsi, $\boxed{y=\mathrm{e}^{-1.428x+1.982}+1}$
d) Si $x=6$ alors, $y=1.001.$ Le degré de salinité estimé au $6^{\text{ième}}$ mois est positif, il est très proche de celui du quatrième mois et lui est inférieur.
Donc, l'équation $y=\mathrm{e}^{-1.428x+1.982}+1$ nous permet de faire cette estimation.
Exercice 2
Le plan est muni d'un repère orthonormal direct $(O\;,\vec{e}_{1}\;,\vec{e}_{2})$
$S=\left(O\;,\ \dfrac{\pi}{2}\;,\ \dfrac{\sqrt{2}}{2}\right)$ est la similitude plane directe de centre $O$, d'angle $\dfrac{\pi}{2}$ et de rapport $\dfrac{\sqrt{2}}{2}.$
Soit $M$ le point d'affixe $z\ $ et $\ M’$ le point d'affixe $z’$ avec $M'=S (M).$
1) Exprimez $z’$ en fonction de $z$
On a : $z'-z=\dfrac{\sqrt{2}}{2}\mathrm{e}^{\mathrm{i}\tfrac{\pi}{2}}(z-z_{0})\ $ or, $z_{0}=0$
Donc, $\boxed{z'=\mathrm{i}\dfrac{\sqrt{2}}{2}z}$
2) On définit la suite des points $(M_{n})_{n\in \mathbb{N}}$ de la façon suivante :
$$\left\lbrace\begin{array}{rcl} M_{0}\ \text {d'affixe}\ z_{0}&=&1+\mathrm{i}\\M_{n}&=&S(M_{n-1})\ \text {pour}\ n\geq 1\end{array}\right.$$
$z_{n}$ est l'affixe de $M_{n}$, pour tout entier naturel $n.$
a) Déterminons les affixes des points $M_{1}\;,\ M_{2}\ $ et $\ M_{3}$
$\begin{array}{rcl} z_{1}&=&\mathrm{i}\dfrac{\sqrt{2}}{2}z_{0}\\ \\&=&\mathrm{i}\dfrac{\sqrt{2}}{2}(1+\mathrm{i})\\ \\&=&\mathrm{i}\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\end{array}$
Donc, $\boxed{z_{1}=\mathrm{i}\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}}$
$\begin{array}{rcl} z_{2}&=&\mathrm{i}\dfrac{\sqrt{2}}{2}z_{1}\\ \\&=&\mathrm{i}\dfrac{\sqrt{2}}{2}\left(\mathrm{i}\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\right)\\ \\&=&-\dfrac{1}{2}-\dfrac{1}{2}\mathrm{i}\end{array}$
Ainsi, $\boxed{z_{2}=-\dfrac{1}{2}-\dfrac{1}{2}\mathrm{i}}$
$\begin{array}{rcl} z_{3}&=&\mathrm{i}\dfrac{\sqrt{2}}{2}z_{2}\\ \\&=&\mathrm{i}\dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}-\dfrac{1}{2}\mathrm{i}\right)\\ \\&=&-\mathrm{i}\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{2}}{4}\end{array}$
D'où, $\boxed{z_{3}=-\mathrm{i}\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{2}}{4}}$
b) Expression de $z_{n}$ en fonction de $z_{n-1}$ pour $n\geq 1.$
On a :
$$\boxed{z_{n}=\mathrm{i}\dfrac{\sqrt{2}}{2}z_{n-1}\;,\quad n\geq 1}$$
c) En déduisons que $z_{n}=\left(\mathrm{i}\dfrac{\sqrt{2}}{2}\right)^{n}z_{0}$
On voit que, d'après (b), $(z_{n})_{n\in\mathbb{N}}$ est une suite géométrique de premier terme $z_{0}=1+\mathrm{i}$ et de raison $q=\mathrm{i}\dfrac{\sqrt{2}}{2}$
D'où, $z_{n}=\left(\mathrm{i}\dfrac{\sqrt{2}}{2}\right)^{n}z_{0}$
Ce qui donne :
$$\boxed{z_{n}=\left(\mathrm{i}\dfrac{\sqrt{2}}{2}\right)^{n}(1+\mathrm{i})\;,\quad n\geq 0}$$
d) Soit $a_{n}=|z_{n}|$, montrons que $a_{n}$ est le terme général d'une suite géométrique dont on précisera la raison et le premier terme.
Soit $a_{n}=|z_{n}|\ $ or,
$\begin{array}{rcl}|z_{n}|&=&\left|\left(\mathrm{i}\dfrac{\sqrt{2}}{2}\right)^{n}(1+\mathrm{i})\right|\\ \\&=&\left|\left(\mathrm{i}\dfrac{\sqrt{2}}{2}\right)^{n}\right|\times|(1+\mathrm{i})|\\ \\&=&\left(\dfrac{\sqrt{2}}{2}\right)^{n}\sqrt{2}\end{array}$
Donc, $\boxed{a_{n}=\sqrt{2}\left(\dfrac{\sqrt{2}}{2}\right)^{n}}$
Par suite :
$\begin{array}{rcl} a_{n+1}&=&\sqrt{2}\left(\dfrac{\sqrt{2}}{2}\right)^{n+1}\\ \\&=&\sqrt{2}\left(\dfrac{\sqrt{2}}{2}\right)^{n}\times\dfrac{\sqrt{2}}{2}\end{array}$
Ainsi,
$$\boxed{a_{n+1}=\dfrac{\sqrt{2}}{2}a_{n}\;,\quad n\geq 0}$$
D'où, $(a_{n})_{n\in\mathbb{N}}$ est une suite géométrique de premier terme $a_{0}=\sqrt{2}$ et de raison $q=\dfrac{\sqrt{2}}{2}$
e) $(a_{n})$ converge vers zéro car sa raison $q=\dfrac{\sqrt{2}}{2}$ est dans $]0\;;\ 1[.$
Problème
Partie A
1) Soit : $\lim_{x\rightarrow 0}\dfrac{\mathrm{e}^{x}-x-1}{x}=\lim_{x\rightarrow 0}\left[\dfrac{\mathrm{e}^{x}-1}{x}-\dfrac{x}{x}\right]$
Or, $\lim_{x\rightarrow 0}\dfrac{\mathrm{e}^{x}-1}{x}=1\ $ et $\ \lim_{x\rightarrow 0}\dfrac{x}{x}=1$
Donc, $\lim_{x\rightarrow 0}\dfrac{\mathrm{e}^{x}-x-1}{x}=1-1=0$
En conclusion :
$$\boxed{\lim_{x\rightarrow 0}\dfrac{\mathrm{e}^{x}-x-1}{x}=0}$$
2)
$$\begin{array}{rcl} k\ :\ ]0\;;\ +\infty[&\longrightarrow&\mathbb{R}\\x&\longmapsto&x(1-\ln x)\end{array}$$
a) $x\mapsto \ln x)$ continue sur $]0\;;\ +\infty[\ $ et $\ x\mapsto 1$ continue sur $\mathbb{R}$ donc, continue sur $]0\;;\ 1[.$
D'où, $x\mapsto x(1-\ln x)$ est continue sur $]0\;;\ 1[$ par somme.
Or, $x\mapsto x$ est continue sur $]0\;;\ 1[$
D'où : par produit, $x\mapsto x(1-\ln x)$ est continue sur $]0\;;\ 1[.$
b)
$$\begin{array}{rcl} K\ :\ ]0\;;\ +\infty[&\longrightarrow&\mathbb{R}\\x&\longmapsto&\dfrac{3}{4}x^{2}-\dfrac{1}{2}x^{2}\ln x\end{array}$$
$x\mapsto \dfrac{3}{4}x^{2}$ est dérivable sur $\mathbb{R}$ donc, elle est dérivable sur $]0\;;\ +\infty[\ $ et $\ x\mapsto\dfrac{1}{2}x^{2}\ln x$ est dérivable sur $]0\;;\ +\infty[$ par produit.
Donc, $K$ est dérivable sur $]0\;;\ +\infty[$ par somme.
Calcul de $K'(x)$
$\begin{array}{rcl} K'(x)&=&\left(\dfrac{3}{4}x^{2}\right)'-\dfrac{1}{2}\left(x^{2}\ln x\right)'\\ \\&=&\dfrac{3}{2}x-\dfrac{1}{2}\left(2x\ln x+x^{2}\left(\dfrac{1}{x}\right)\right)\\ \\&=&\dfrac{3}{2}x-x\ln x-\dfrac{1}{2}x\\ \\&=&x-x\ln x\end{array}$
D'où : $\boxed{K'(x)=k(x)}$
Partie B
Soit $f(x)=\left\lbrace\begin{array}{rcrcl}\mathrm{e}^{x}-x-1&\text{si}&x&\leq&0\\x\ln x&\text{si}&x&>&0\end{array}\right.$
1) Si $x\leq 0$ alors, $\mathrm{e}^{x}-x-1$ existe et si $x>0$ alors, $x\ln x$ existe.
D'où, $f(x)$ existe si $x\in\;]-\infty\;;\ 0]\cup]0\;;\ +\infty[.$
Ainsi, $\boxed{D_{f}=]-\infty\;;\ +\infty[}$
$$\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}\mathrm{e}^{x}-x-1=+\infty$$
$$\lim_{x\rightarrow 0^{-}}f(x)=f(0)=0,$$
$$\lim_{x\rightarrow 0^{+}}f(x)=\lim_{x\rightarrow 0^{+}}x\ln x\quad\text{or, }\ \lim_{x\rightarrow 0^{+}}x\ln x=0$$
D'où :
$$\boxed{\lim_{x\rightarrow 0^{+}}f(x)=0}$$
$$\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}x\ln x=+\infty$$
2) a) $f$ est définie en $0$ car dans $[0\;;\ +\infty[\;,\ f(x)=\mathrm{e}^{x}-x-1\ $ et $\ x\mapsto \mathrm{e}^{x}-x-1$ est définie en $0$ et prend la valeur $0$, on a alors :
$$f(0)=0$$
$$\lim_{x\rightarrow 0^{-}}f(x)=0\quad \text{et}\quad \lim_{x\rightarrow 0^{+}}f(x)=0$$
D'où :
$$\boxed{\lim_{x\rightarrow 0^{-}}f(x)=\lim_{x\rightarrow 0^{+}}f(x)=f(0)}$$
Ainsi, $f$ est continue en $0.$
b) D'après la partie A, on a :
$$\lim_{x\mapsto 0^{-}}\dfrac{f(x)-f(0)}{x}=\lim_{x\mapsto 0^{-}}\dfrac{\mathrm{e}^{x}-x-1}{x}=0$$
Par ailleurs,
$$\lim_{x\mapsto 0^{+}}\dfrac{f(x)-f(0)}{x}=\lim_{x\mapsto 0^{+}}\ln x=-\infty$$
Donc, $f$ n'est pas dérivable en $0$ car ne l'étant pas en $0$ à droite.
Interprétation graphique :
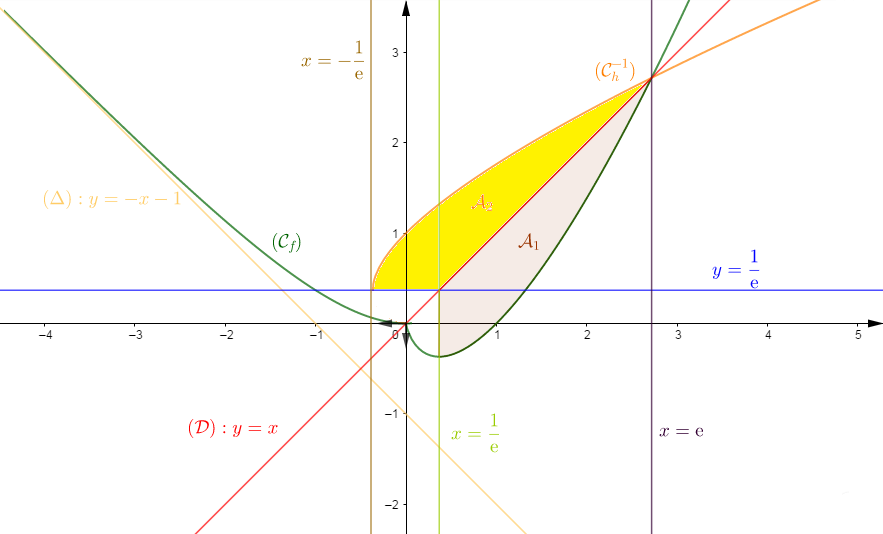
La courbe représentative de $f\;,\ (\mathcal{C}_{f}),$ admet au point d'abscisse $0$ une demi-tangente d'équation $x=0$ à gauche et une demi-tangente d'équation $y=0$ à droite.
3) $x\mapsto \mathrm{e}^{x}\ $ et $\ x\mapsto -x-1$ sont continues sur $\mathbb{R}$ donc, sur $]-\infty\;;\ 0[,$
$x\mapsto x\ln x$ continue sur $]0\;;\ +\infty[$ par produit et $f$ est continue en $0.$
Donc, $f$ est continue sur $\mathbb{R}.$
$x\mapsto \mathrm{e}^{x}\ $ et $\ x\mapsto -x-1$ sont dérivables sur $\mathbb{R}$ donc, sur $]-\infty\;;\ 0[,$
$x\mapsto x\ln x$ dérivable sur $]0\;;\ +\infty[$ par produit.
Donc, $f$ est dérivable sur $\mathbb{R}\setminus \{0\}.$
4) Pour $x<0\;,\ f'(x)=\mathrm{e}^{x}-1\ $ or, si $x<0$ alors, $\mathrm{e}^{x}<1$
D'où, $f'(x)<0\ $ pour $\ x<0$
Pour $x>0\;,\ f'(x)=\ln x+1$
Or, $\ \ln x+1\geq 0\ $ si $\ x\in \left[\dfrac{1}{\mathrm{e}}\;;\ +\infty\right[\ $ et $\ \ln x+1\leq 0\ $ si $\ x\in \left[0\;;\ \dfrac{1}{\mathrm{e}}\right]$
D'où, $f'(x)\geq 0\ $ pour $\ x\in \left[\dfrac{1}{\mathrm{e}}\;;\ +\infty\right[\ $ et $\ f'(x)\leq 0\ $ pour $\ x\in \left[0\;;\ \dfrac{1}{\mathrm{e}}\right[$
5) Dressons son tableau de variations.
$$\begin{array}{|c|lcccccr|}\hline x&-\infty&&0&&1/\mathrm{e}&&+\infty\\ \hline f'(x)&&-&||&-&0&+&\\ \hline&+\infty&&\vdots&&\vdots&&+\infty\\&&\searrow&\vdots&&\vdots&&\\f&&&0&&\vdots&\nearrow&\\&&&\vdots&\searrow&\vdots&&\\&&&\vdots&&-1/\mathrm{e}&&\\ \hline\end{array}$$
6) $f(x)-(-x-1)=\mathrm{e}^{x}$
D'où :
$$\lim_{x\rightarrow -\infty}f(x)-(-x-1)=\lim_{x\rightarrow -\infty}\mathrm{e}^{x}=0$$
Donc, $\Delta : y=-x-1$ est asymptote à $(\mathcal{C}_{f})$ au voisinage de $-\infty$
7) $\lim_{x\rightarrow +\infty}f(x)=+\infty$ donc, $(\mathcal{C}_{f}$ admet une branche infinie au voisinage de $+\infty$
$\lim_{x\rightarrow +\infty}\dfrac{f(x)}{x}=\lim_{x\rightarrow +\infty}\ln x=+\infty$ donc, $(\mathcal{C}_{f})$ admet une branche parabolique de direction $(y'Oy)$ au voisinage de $+\infty$
8) Traçons la courbe $(\mathcal{C}_{f})$ de $f$ dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$ d'unité graphique $2\;cm$
9) Soit $h$ la restriction de $f$ à $\left[\dfrac{1}{\mathrm{e}}\;;\ +\infty\right[$
a) Dressons le tableau de variations de $h.$
$$\begin{array}{|c|lcccr|}\hline x&1/\mathrm{e}&&1&&+\infty\\ \hline h'(x)&&+&&+&\\ \hline&&&\vdots&&+\infty\\&&&\vdots&\nearrow&\\h&&&0&&\\&&\nearrow&\vdots&&\\&-1/\mathrm{e}&&\vdots&&\\ \hline\end{array}$$
$h$ est continue et strictement croissante sur $\left[\dfrac{1}{\mathrm{e}}\;;\ +\infty\right[$, donc elle est bijective. Elle réalise une bijection de $\left[\dfrac{1}{\mathrm{e}}\;;\ +\infty\right[$ vers $J=\left[-\dfrac{1}{\mathrm{e}}\;;\ +\infty\right[$ d'après le tableau de variations de $f.$
b) Pour la courbe $(\mathcal{C}_{h}^{-1})$ de $h^{-1}$, bijection réciproque de $h$, voir figure.
10) a) Ce domaine est l'ensemble des points $M(x\;;\ y)$ tels que :
$$\dfrac{1}{\mathrm{e}}\leq x\leq \mathrm{e}\quad \text{et}\quad h(x)\leq y\leq x$$
On a donc :
\begin{eqnarray}\mathcal{A}_{1}&=&\int_{\tfrac{1}{\mathrm{e}}}^{\mathrm{e}}(x-h(x))\mathrm{d}x\nonumber \\&=&\int_{\tfrac{1}{\mathrm{e}}}^{\mathrm{e}}(x-x\ln x)\mathrm{d}x\nonumber \\&=&\int_{\tfrac{1}{\mathrm{e}}}^{\mathrm{e}}k(x)\mathrm{d}x \nonumber \end{eqnarray}
Or, d'après la Partie A, $K(x)$ est une primitive de $k(x)$ donc :
$$\int_{\tfrac{1}{\mathrm{e}}}^{\mathrm{e}}k(x)dx=\left[K(x)\right]_{\tfrac{1}{\mathrm{e}}}^{\mathrm{e}}$$
Par suite :
$\begin{array}{rcl}\mathcal{A}_{1}&=&\left[K(x)\right]_{\tfrac{1}{\mathrm{e}}}^{\mathrm{e}}\\ \\&=&\left( K(\mathrm{e})-K\left((\dfrac{1}{\mathrm{e}}\right)\right)\times\text{u.a}\\ \\&=&\left( \dfrac{3}{4}\mathrm{e}^{2}-\dfrac{1}{2}\mathrm{e}^{2}\ln \mathrm{e}-\left(\dfrac{3}{4\mathrm{e}^{2}}-\dfrac{1}{2\mathrm{e}^{2}}\ln\dfrac{1}{\mathrm{e}}\right)\right)\times\text{u.a}\\ \\&=&\left(\dfrac{3}{4}\mathrm{e}^{2}-\dfrac{1}{2}\mathrm{e}^{2}-\dfrac{3}{4\mathrm{e}^{2}}-\dfrac{1}{2\mathrm{e}^{2}}\right)\times\text{u.a}\\ \\&=&\dfrac{1}{4}\left(\mathrm{e}^{2}-\dfrac{5}{\mathrm{e}^{2}}\right)\times\text{u.a}\end{array}$
Or, on a choisit comme unité graphique $2\;cm$ donc,
$$\text{u.a}=2\;cm\times 2\;cm=4\;cm^{2}$$
Ainsi,
$$\boxed{\mathcal{A}_{1}=\left(\mathrm{e}^{2}-\dfrac{5}{\mathrm{e}^{2}}\right)=6.72\;cm^{2}}$$
b) Ce domaine est le symétrique, par rapport à la première bissectrice, du domaine d'aire $\mathcal{A}_{1}$ de la question 10) a)
D'où :
$$\boxed{\mathcal{A}_{2}=\mathcal{A}_{1}=6.72\;cm^{2}}$$

Ajouter un commentaire