Corrigé devoir n°41 maths - 2nd S
Classe:
Seconde
Exercice 1
1. Développer le membre de gauche, puis simplifier.
2. Diviser les deux membres de l'égalité précédente par $(a-1).$
3. Remplacer $a$ par $\dfrac{1}{2}.$
On obtient $S=\dfrac{\left(\dfrac{1}{2}\right)^{5}-1}{\dfrac{1}{2}-1}=\boxed{31}$
Exercice 2
1. $a^{2}=x^{2}+\dfrac{1}{x^{2}}+2$ d'après une formule d'identité remarquable.
On en déduit aussitôt l'égalité en transposant $2$ dans le membre de gauche.
\begin{eqnarray}2.\quad(y-2)^{2}&=&\left(\sqrt{7+4\sqrt{3}}-\sqrt{7-4\sqrt{3}}\right)^{2}\nonumber\\\\&=&7+4\sqrt{3}+7-4\sqrt{3}-2\sqrt{(\sqrt{7+4\sqrt{3}}\times \sqrt{7-4\sqrt{3}}}\nonumber\\\\&=&14-2\sqrt{49-48}\nonumber\\\\&=&14-2\nonumber\\\\&=&12 \end{eqnarray}
D'où $Y^{2}-4Y+4=12$, Soit $Y^{2}-4Y-8=0$
3. $X^{2}=(Y-2)^{2}=12$ d'après un calcul déjà effectué.
Or $X$ est positif car $7+4\sqrt{3}>7-4\sqrt{3}.$
Donc $X=\sqrt{12}=2\sqrt{3}$
$Y$ est supérieur à $2$, donc $Y-2=X$,, d'où $Y=2+2\sqrt{3}$
Exercice 3
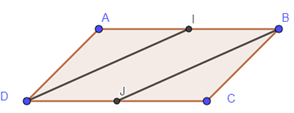
1. On a par définition de $I$ et $J$ : $\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}$ et $\overrightarrow{DJ}=\dfrac{1}{2}\overrightarrow{DC}.$
Or, $\overrightarrow{AB}=\overrightarrow{DC}$ puisque $ABCD$ est un parallélogramme.
Donc $\overrightarrow{IB}=\overrightarrow{DJ}$ et par conséquent le quadrilatère $IBJD$ ou $(DIBJ)$ est aussi un parallélogramme.
Par suite $\overrightarrow{DI}=\overrightarrow{JB}$
2. a. Voir figure ci-dessous.
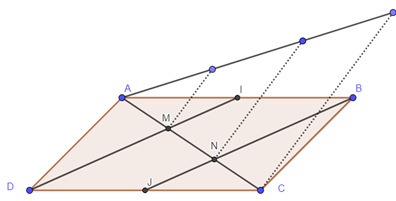
b. $\overrightarrow{IM}=\overrightarrow{IA}+\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}$
$\begin{array}{lll} \overrightarrow{ID}&=&\overrightarrow{IA}+\overrightarrow{AD}\\&=&-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}\\&=&-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}\\&=&-\dfrac{3}{2} \overrightarrow{AB}+\overrightarrow{AC}\end{array}$
Il en résulte que $\overrightarrow{ID}=3\overrightarrow{IM}$ et par conséquent les points $I$, $D$ et $M$ sont alignés.
$\begin{array}{lll}\text{c.}\quad\overrightarrow{JN}&=&\overrightarrow{JC}+\overrightarrow{CN}\\&=&\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{CA}\\&=&\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}\end{array}$
$\begin{array}{lll}\text{d.}\quad\overrightarrow{JB}&=&\overrightarrow{JC}+\overrightarrow{CB}\\&=&\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{AB}\\&=&\dfrac{3}{2}\overrightarrow{AB}-\overrightarrow{AC}\end{array}$
D'où $\overrightarrow{JB}=3\overrightarrow{JN}$ et l'alignement des points $J$, $B$ et $N$
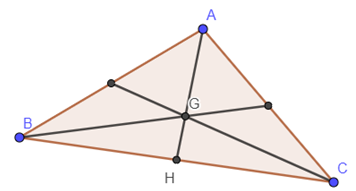
3.
$\bullet\ $Introduire $G$ dans $\overrightarrow{MA}$, $\overrightarrow{MB}$ et $\overrightarrow{MC}$ et tenir compte du fait que $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$
$\bullet\ $Introduire $H$ dans $2\overrightarrow{MA}$, $\overrightarrow{MB}$ et $\overrightarrow{MC}$ et utiliser le fait que $\overrightarrow{HB}+\overrightarrow{HC}=\overrightarrow{0}$

Ajouter un commentaire