Corrigé Exercice 1 : Théorème de Thalès - 3e

 

Calculons $x$ dans les cas suivants :

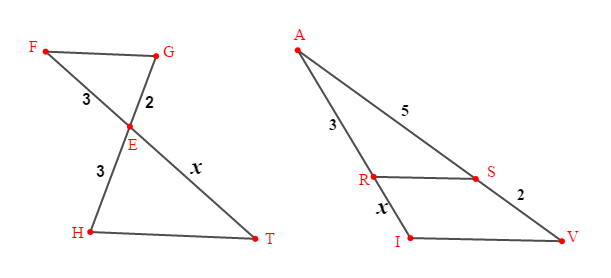
Dans le premier cas, les droites $(FT)\ $ et $\ (HG)$ sécantes en $E$ sont coupées par deux droites parallèles $(FG)\ $ et $\ (HT)$ donc, d'après le théorème de Thalès on a : $$\dfrac{EF}{ET}=\dfrac{EG}{EH}=\dfrac{FG}{HT}$$

 

Par suite, 

 

$\begin{array}{rcl}\dfrac{EF}{ET}=\dfrac{EG}{EH}&\Rightarrow&\dfrac{3}{x}=\dfrac{2}{3}\\ \\&\Rightarrow&2x=9\\ \\&\Rightarrow&x=\dfrac{9}{2}\end{array}$

 

D'où, $\boxed{x=\dfrac{9}{2}}$

 

Dans le deuxième cas, les droites $(AI)\ $ et $\ (AV)$ sécantes en $A$ sont coupées par deux droites parallèles $(RS)\ $ et $\ (IV)$ donc, les triangles $ARS\ $ et $\ AIV$ sont en position de Thalès.

 

Ainsi, en appliquant le théorème de Thalès, on obtient : $$\dfrac{AR}{AI}=\dfrac{AS}{AV}=\dfrac{RS}{IV}$$

 

Par suite,

 

$\begin{array}{rcl}\dfrac{AR}{AI}=\dfrac{AS}{AV}&\Rightarrow&\dfrac{3}{3+x}=\dfrac{5}{7}\\ \\&\Rightarrow&5(3+x)=21\\ \\&\Rightarrow&5x=21-15\\ \\&\Rightarrow&x=\dfrac{6}{5}\end{array}$

 

D'où, $\boxed{x=\dfrac{6}{5}}$