Corrigé Exercice 11 : Distances - 4e

 

Soit un cercle $\mathcal{C}(M\;;\ 2\;cm).\ A\ $ et $\ B$ sont deux points de $(\mathcal{C})$ non diamétralement opposés. La droite $(d_{1})$ est tangente à $(\mathcal{C})$ en $A.$ La droite $(d_{2})$ est tangente à $(\mathcal{C})$ en $B.$ Les droites $(d_{1})\ $ et $\ (d_{2})$ se coupent en $C.$

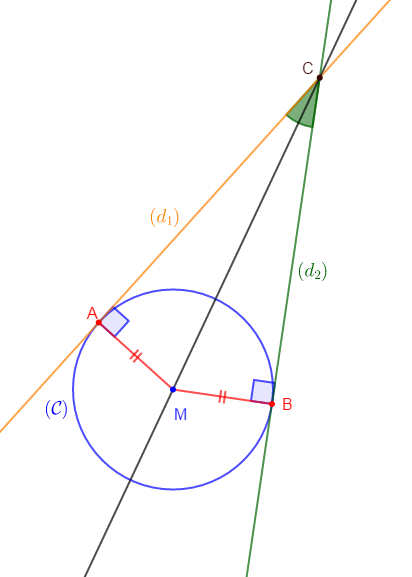
Démontrons que le point $M$ appartient à la bissectrice de l'angle $ACB.$

 

En effet, on sait que si un point $M$ est équidistant des supports des deux côtés d'un angle alors, ce point appartient à la bissectrice de cet angle.

 

Donc, dans cet exercice, il suffit de montrer que $M$ est équidistant des demi-droites $[CA)\ $ et $\ [CB)$ qui sont les supports des côtés de l'angle $\widehat{ACB}.$

 

On a :

 

$(d_{1})$ est tangente à $(\mathcal{C})$ en $A$ donc, $(d_{1})$ est perpendiculaire à $[MA]$ en $A.$

 

D'où, la distance de $M$ à $(d_{1})$ est égale à $MA.$

 

Par suite, la distance de $M$ à $[CA)$ est égale à $MA.$

 

De la même manière, on a :

 

$(d_{2})$ tangente à $(\mathcal{C})$ en $B$ alors, $(d_{2})$ est perpendiculaire à $[MB]$ en $B.$

 

Donc, la distance de $M$ à $(d_{2})$ est égale à $MB.$

 

Ainsi, la distance de $M$ à $[CB)$ est égale à $MB.$

 

Or, on sait que $MA=MB$ car $A\ $ et $\ B$ appartiennent au cercle $(\mathcal{C}).$

 

Par suite,

$$\text{distance de }M\text{ à }[CA)=\text{distance de }M\text{ à }[CB)$$

Ce qui signifie que $M$ est équidistant des supports des deux côtés de l'angle $\widehat{ACB}.$

 

D'où, le point $M$ appartient à la bissectrice de l'angle $\widehat{ACB}.$