Corrigé Exercice 11 : Théorème de Thalès - 3e

 

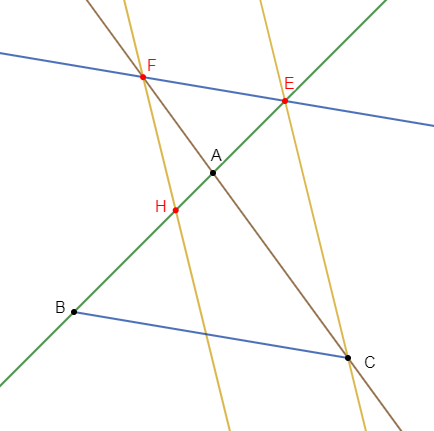
$ABC$ est un triangle $E$ est un point de la droite$(AB).$

 

La droite passant par $E$ et parallèle à la droite $(BC)$ coupe la droite $(AC)$ au point $F.$

 

La droite passant par $F$ et parallèle à la droite $(EC)$ coupe la droite $(AB)$ au point $H.$

 

Démontrons que $AE^{2}=AH\times AB.$

 

En effet, les droites $(BC)\ $ et $\ (EF)$ étant parallèles alors, les triangles $AEF\ $ et $\ ABC$ sont en position de Thalès.

 

Donc, en appliquant le théorème de Thalès, on a :

$$\dfrac{AE}{AB}=\dfrac{AF}{AC}\quad(1)$$

De la même manière, les droites $(FH)\ $ et $\ (EC)$ étant parallèles alors, les triangles $AFH\ $ et $\ AEC$ sont en position de Thalès.

 

Ainsi, d'après le théorème de Thalès, on a :

$$\dfrac{AH}{AE}=\dfrac{AF}{AC}\quad(2)$$

En comparant les égalités $(1)\ $ et $\ (2)$, on peut alors écrire :

$$\dfrac{AE}{AB}=\dfrac{AH}{AE}$$

Par suite,

 

$\begin{array}{rcl}\dfrac{AE}{AB}=\dfrac{AH}{AE}&\Leftrightarrow&AE\times AE=AH\times AB\\\\&\Leftrightarrow&AE^{2}=AH\times AB\end{array}$

 

D'où, $\boxed{AE^{2}=AH\times AB}$