Corrigé Exercice 12 : Distances - 4e

 

Les boucles d'oreille de la petite Sassoum sont formées de petits cercles $\mathcal{C}_{1}\;;\ \mathcal{C}_{2}$ et $\mathcal{C}_{3}$ tels que : $$\mathcal{C}_{1}(I\;;\ r_{1}=0.2)\;;\ \mathcal{C}_{2}(J\;;\ r_{2}=0.3)\ \text{ et }\ \mathcal{C}_{3}(K\;;\ r_{3}=0.5)$$

Les points $I\;,\ J\ $ et $\ K$ sont alignés dans cet ordre tels que $IJ=JK=0.1$

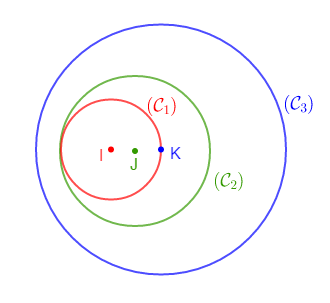
Déterminons la position relative des cercles :

 

1) $\mathcal{C}_{1}\ $ et $\ \mathcal{C}_{2}$ sont tangents intérieurement.

 

Pour la justification, on doit vérifier que $IJ=|r_{1}-r_{2}|$

 

En effet, on a : $IJ=0.1$

 

De plus,

 

$\begin{array}{rcl} |r_{1}-r_{2}|&=&|0.2-0.3|\\\\&=&|-0.1|\\\\&=&0.1\end{array}$

 

Donc, $|r_{1}-r_{2}|=0.1$

 

Ainsi, $IJ=|r_{1}-r_{2}|$

 

Ce qui montre que les cercles $\mathcal{C}_{1}(I\;;\ r_{1})\ $ et $\ \mathcal{C}_{2}(J\;;\ r_{2})$ sont tangents intérieurement.

 

2) $\mathcal{C}_{2}\ $ et $\ \mathcal{C}_{3}$ sont disjoints intérieurement.

 

Pour la justification, il suffit de vérifier que $JK<|r_{2}-r_{3}|$

 

Soit : $JK=0.1\;,\ r_{2}=0.3\ $ et $\ r_{3}=0.5$

 

Alors, on a :

 

$\begin{array}{rcl} |r_{2}-r_{3}|&=&|0.3-0.5|\\\\&=&|-0.2|\\\\&=&0.2\end{array}$

 

Donc, $|r_{2}-r_{3}|=0.2$

 

Par suite, $JK<|r_{2}-r_{3}|$

 

Par conséquent, les cercles $\mathcal{C}_{2}(J\;;\ r_{2})\ $ et $\ \mathcal{C}_{3}(K\;;\ r_{3})$ sont disjoints intérieurement.

 

3) $\mathcal{C}_{1}\ $ et $\ \mathcal{C}_{3}$ sont disjoints intérieurement.

 

Pour la justification, on doit vérifier que $IK<|r_{1}-r_{3}|$

 

En effet, comme $J\in[IK]$ alors,

 

$\begin{array}{rcl} IK&=&IJ+JK\\\\&=&0.1+0.1\\\\&=&0.2\end{array}$

 

Donc, $IK=0.2$

 

Aussi,

 

$\begin{array}{rcl} |r_{1}-r_{3}|&=&|0.1-0.5|\\\\&=&|-0.4|\\\\&=&0.4\end{array}$

 

Donc, $|r_{1}-r_{3}|=0.4$

 

Ainsi, $IK<|r_{1}-r_{3}|$

 

Ce qui prouve que les cercles $\mathcal{C}_{1}(I\;;\ r_{1})\ $ et $\ \mathcal{C}_{3}(K\;;\ r_{3})$ sont disjoints intérieurement.