Corrigé Exercice 13 : Distances - 4e

 

Soit $O\;;\ I\;;\ J\;;\ K\;;\ L$ des points d'une droite $(d)$ tels que :

 

$OI=4\;cm\;;\quad OJ=6\;cm\;;\quad OK=8\;cm\;;\quad OL=5\;cm$

 

$O\in[IL]\;;\quad O\notin[IJ]\;;\quad O\notin[IK].$

 

1) Construisons le cercle $\mathcal{C}$ de centre $O$ et de $5\;cm$ de rayon.

 

2) Traçons les perpendiculaires $(d_{1})\;;\ (d_{2})\;;\ (d_{3})\ $ et $\ (d_{4})$ à la droite $(d)$ respectivement en $I\;;\ J\;;\ K\ $ et $\ L.$

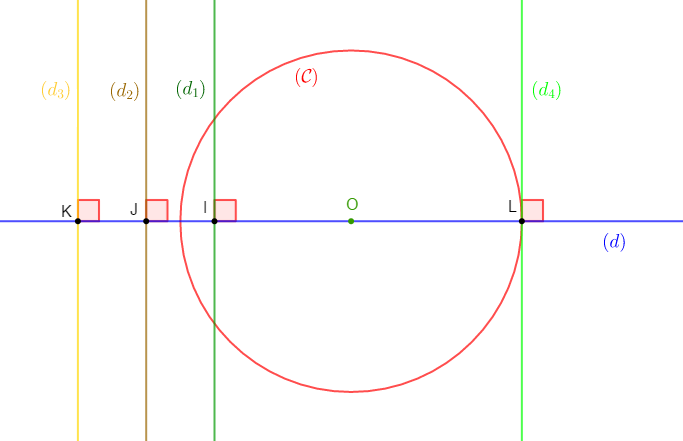
3) Déterminons la position relative de chacune de ces droites par rapport au cercle $(\mathcal{C})$

 

$-\ \ (d_{1})\ $ et $\ (\mathcal{C})$ sont sécants.

 

En effet, soit $OI$ la distance du point $O$ à la droite $(d_{1}).$

 

Comme $OI$ est inférieure au rayon du cercle $(\mathcal{C})$ de centre $O$ alors, $(d_{1})\ $ et $\ (\mathcal{C})$ sont sécants.

 

$-\ \ (d_{2})\ $ et $\ (\mathcal{C})$ sont disjoints.

 

Soit $OJ$ la distance du point $O$ à la droite $(d_{2}).$

 

Or, $OJ$ est supérieure au rayon du cercle $(\mathcal{C})$ de centre $O.$

 

Par conséquent, la droite $(d_{2})\ $ et $\ (\mathcal{C})$ sont disjoints.

 

$-\ \ (d_{3})\ $ et $\ (\mathcal{C})$ sont disjoints

 

Soit $OK$ la distance du point $O$ à la droite $(d_{3}).$

 

Comme $OK$ est supérieure au rayon du cercle $(\mathcal{C})$ de centre $O$ alors, $(d_{3})\ $ et $\ (\mathcal{C})$ sont disjoints.

 

$-\ \ (d_{4})\ $ et $\ (\mathcal{C})$ sont tangents en $L.$

 

$OL$ est la distance du point $O$ à la droite $(d_{4}).$

 

Or, $OL$ est égale au rayon du cercle $(\mathcal{C})$ de centre $O.$

 

Donc, la droite $(d_{4})\ $ et $\ (\mathcal{C})$ sont tangents en $L.$