Corrigé Exercice 14 : Distances - 4e

 

$ABC$ est un triangle. La droite $(d)$ est la parallèle à $(BC)$ qui passe par $A.$ La médiatrice de $[AB]$ coupe la droite $(d)$ en $P.$

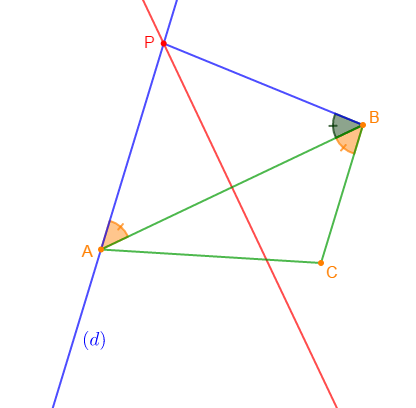
1) Démontrons que les angles $\widehat{PAB}\ $ et $\ \widehat{CBA}$ ont des mesures égales.

 

En effet, $(d)\ $ et $\ (BC)$ sont deux droites parallèles coupées par la même sécante $(AB).$

 

Or, on sait que deux droites parallèles coupées par une sécante déterminent deux angles alternes internes de même mesure.

 

Donc, $\widehat{PAB}\ $ et $\ \widehat{CBA}$ sont deux angles alternes internes de même mesure.

 

D'où,

$$mes\;(\widehat{PAB})=mes\;(\widehat{CBA})$$

2) Démontrons que $PAB$ est isocèle en $P.$

 

On a : $P$ appartient à la médiatrice de $[AB].$

 

Or, on sait que tout point appartenant à la médiatrice d'un segment est équidistant des extrémités de ce segment.

 

Donc, le point $P$ est équidistant des points $A\ $ et $\ B.$

 

Ce qui signifie alors : $PA=PB$

 

Par conséquent, le triangle $PAB$ est isocèle en $P$ car, ses deux côtés $[PA]\ $ et $\ [PB]$ ont la même longueur.

 

3) Démontrons que la droite $(AB)$ est bissectrice de l'angle $\widehat{PBC}.$

 

Comme le triangle $PAB$ est isocèle en $P$ alors, les angles $\widehat{PAB}\ $ et $\ \widehat{PBA}$ ont des mesures égales.

 

Ce qui signifie : $$mes\;(\widehat{PAB})=mes\;(\widehat{PBA})\qquad\text{égalité 1}$$

Par ailleurs, on avait montré à la question 1) que $mes\;(\widehat{PAB})=mes\;(\widehat{CBA})$

 

Donc, en remplaçant $mes\;(\widehat{PAB})$ par $mes\;(\widehat{CBA})$ dans l'égalité $1$, on obtient :

$$mes\;(\widehat{CBA})=mes\;(\widehat{PBA})\qquad\text{égalité 2}$$

Par suite, $\widehat{PAB}\ $ et $\ \widehat{CBA}$ sont deux angles adjacents de même mesure et qui ont en commun le côté $(AB)$

 

Ainsi, la droite $(AB)$ passe par le sommet $B$ de l'angle $\widehat{PBC}$ et partage cet angle en deux angles de même mesure.

 

Par conséquent, la droite $(AB)$ est bissectrice de l'angle $\widehat{PBC}.$