Corrigé Exercice 15 : Symétrie centrale 5e
Classe:
Cinquième
Exercice 15
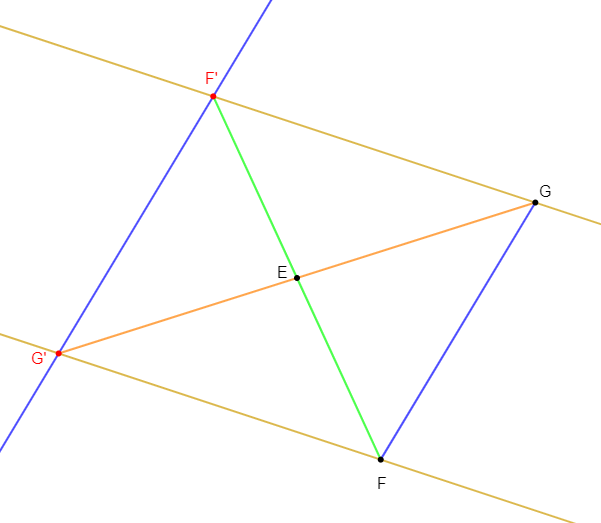
1) Construisons le triangle $EFG$ tel que
$$EF=4\;cm\;;\ FG=6\;cm\ \text{ et }\ EG=5\;cm$$
2) a) Plaçons le point $F'$ symétrique du point $F$ par rapport à $E.$
b) Plaçons le point $G'$ symétrique du point $G$ par rapport à $E.$
3) Les droites $(FG)\ $ et $\ (F'G')$ sont parallèles.
Justifions notre réponse.
On a : $S_{E}(F)=F'\;;\ S_{E}(G)=G'\;;\ S_{C}(C)=C$
Alors, $S_{E}((FG))=(F'G')$
Ce qui signifie que la droite $(F'G')$ est le symétrique de la droite $(FG)$ par rapport au point $E.$
Or, on sait que : le symétrique d'une droite est droite qui lui est parallèle.
Par conséquent, les droites $(FG)\ $ et $\ (F'G')$ sont parallèles.
4) Donnons, sans les mesurer, les longueurs $EF'\;,\ EG'\ $ et $\ F'G'.$
On a :
$$EF'=4\;cm\;;\ EG'=5\;cm\ \text{ et }\ F'G'=6\;cm$$
Justifions notre réponse.
Comme $F'$ symétrique de $F$ par rapport à $E$ alors, $E$ est milieu du segment $[FF']$ et on a : $EF'=EF$
D'où, $\boxed{EF'=4\;cm}$
Comme $G'$ symétrique de $G$ par rapport à $E$ alors, $E$ est milieu du segment $[GG']$ et on a : $EG'=EG$
D'où, $\boxed{EG'=5\;cm}$
On a : $[F'G']$ est le symétrique de $[FG]$ par rapport à $E.$
Or, on sait que : le symétrique d'un segment par rapport à un point est un segment de même longueur.
Ce qui signifie que $F'G'=FG$
Par conséquent, $\boxed{F'G'=6\;cm}$
5) Prouvons que les droites $(F'G)\ $ et $\ (FG')$ sont parallèles.
On a : $F\ $ et $\ F'$ sont symétriques par rapport à $E.$
Donc, $S_{E}(F')=F$
Aussi, on a : $G\ $ et $\ G'$ sont symétriques par rapport à $E.$
Alors, $S_{E}(G)=G'$
Ce qui donne alors, $S_{E}((F'G))=(FG')$
Ce qui signifie que la droite $(F'G)$ est le symétrique de la droite $(FG')$ par rapport au point $E.$
Or, on sait que : le symétrique d'une droite est droite qui lui est parallèle.
Par conséquent, les droites $(F'G)\ $ et $\ (FG')$ sont parallèles.

Ajouter un commentaire