Corrigé Exercice 15 : Théorème de Thalès - 3e

 

1) Soit un cercle $(\zeta)$ de centre $O$ et de rayon $4\,cm\;,\ [AD]$ un de ses diamètres.

 

a) D'un côté de la droite $(AD)$, construisons le point $G$ tel que le triangle $ADG$ soit équilatéral.

 

b) De l'autre côté de la droite $(AD)$, plaçons le point $B$ du cercle $(\zeta)$, tel que $AB=4\,cm.$

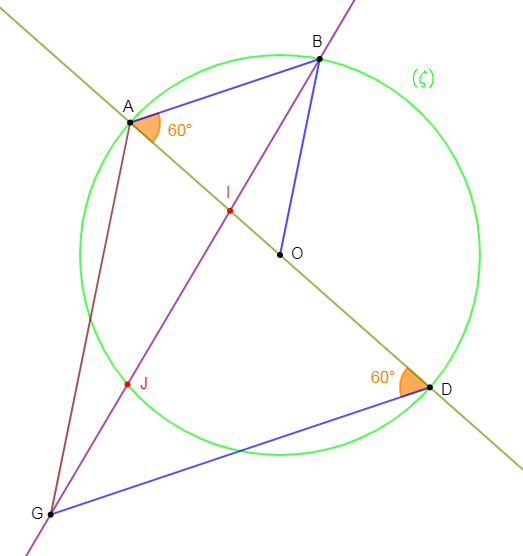
2) Démontrons que le triangle $OAB$ est équilatéral.

 

En effet, comme $A\ $ et $\ B$ appartiennent au cercle $(\zeta)$ alors, les longueurs $OA\ $ et $\ OB$ sont égales au rayon de $(\zeta).$

 

Ce qui signifie que : $OA=OB=4\,cm$

 

De plus, on sait que : $AB=4\,cm$

 

Donc,

$$OA=OB=AB=4\,cm$$

Ainsi, le triangle $OAB$ a ses côtés de même longueur par conséquent, c'est un triangle équilatéral.

 

3) On admet que les angles $\widehat{OAB}\ $ et $\ \widehat{ADG}$ sont égaux. En déduisons la position relative de $(AB)\ $ et $\ (DG).$

 

En effet, les droites $(AB)\ $ et $\ (DG)$ et la sécante $(AD)$ déterminent deux angles alternes internes $\widehat{OAB}\ $ et $\ \widehat{ADG}.$

 

Comme ces deux angles sont de même mesure alors, les droites $(AB)\ $ et $\ (DG)$ sont parallèles.

 

4) La droite $(BG)$ coupe le segment $[AD]$ en $I\ $ et $\ (\zeta)$ en $J.$ En utilisant le théorème de Thalès justifions que : $$\dfrac{IA}{ID}=\dfrac{1}{2}$$

 

En effet, les droites $(AD)\ $ et $\ (BG)$ sécantes en $I$ sont coupées par deux droites $(AB)\ $ et $\ (DG).$

 

Or, d'après le résultat de la question $3)$, on a : $(AB)\ $ et $\ (DG)$ sont parallèles.

 

Donc, les triangles $AIB\ $ et $\ DIG$ sont en position de Thalès.

 

Ainsi, en utilisant le théorème de Thalès, on a :

$$\dfrac{IA}{ID}=\dfrac{AB}{DG}$$

Or, on sait que $ADG$ est un triangle équilatéral.

 

Par conséquent : $DG=AD$

 

Comme $[AD]$ est un diamètre de $(\zeta)$ alors, la longueur $AD$ est égale au double du rayon de $(\zeta).$

 

Donc, $AD=2\times 4\,cm=8\,cm$

 

Par suite, $DG=8\,cm$

 

Ainsi, dans l'égalité $\dfrac{IA}{ID}=\dfrac{AB}{DG}$, en remplaçant $AB\ $ et $\ DG$ par leur valeur, on obtient :

 

$\begin{array}{rcl}\dfrac{IA}{ID}&=&\dfrac{AB}{DG}\\\\&=&\dfrac{4}{8}\\\\&=&\dfrac{4\div 4}{8\div 4}\\\\&=&\dfrac{1}{2}\end{array}$

 

D'où, $\boxed{\dfrac{IA}{ID}=\dfrac{1}{2}}$