Corrigé Exercice 16 : Théorème de Thalès - 3e

 

Construisons un rectangle $ABCD$ tel que : $AB=8\;cm\ $ et $\ AD=6\;cm.$ On désigne par $M$ un point $[AB]$ tel que $AM=x.$

 

Par $M$, on trace la parallèle à $(AC)$ qui coupe $(BC)$ en $N$ et la parallèle à $(BD)$ qui coupe $(AD)$ en $P.$

 

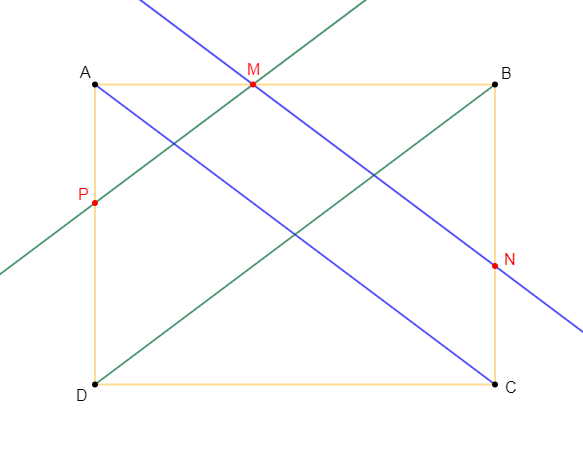
1) Calculons $AC$ puis exprimons $MN\ $ et $\ MP$ en fonction de $x.$

 

$-\ $ Calcul de $AC$

 

Comme $ABCD$ est un rectangle alors, le triangle $ABC$ est rectangle en $B.$

 

Donc, en utilisant le théorème Pythagore, on a :

 

$\begin{array}{rcl} AC^{2}=AB^{2}+CC^{2}&\Rightarrow&AC=\sqrt{AB^{2}+BC^{2}}\\\\&\Rightarrow&AC=\sqrt{8^{2}+6^{2}}\\\\&\Rightarrow&AC=\sqrt{64+36}\\\\&\Rightarrow&AC=\sqrt{100}\\\\&\Rightarrow&AC=10\end{array}$

 

D'où, $\boxed{AC=10\,cm}$

 

$-\ $ Expression de $MN$ en fonction de $x$x

 

Les droites $(MN)\ $ et $\ (AC)$ étant parallèles alors, les triangles $BNM\ $ et $\ BAC$ sont en position de Thalès.

 

Ainsi, d'après le théorème de Thalès, on obtient : $$\dfrac{MN}{AC}=\dfrac{MB}{AB}$$

 

Or, on sait que : $MB=AB-AM$

 

Donc, en remplaçant $MB$ par $AB-AM$, on trouve : $\dfrac{MN}{AC}=\dfrac{AB-AM}{AB}$

 

Par suite, en remplaçant $AC\;,\ AB\ $ et $\ AM$ par leur valeur, on obtient :

 

$\begin{array}{rcl}\dfrac{MN}{AC}=\dfrac{AB-AM}{AB}&\Rightarrow&\dfrac{MN}{10}=\dfrac{8-x}{8}\\\\&\Rightarrow&8\times MN=10\times(8-x)\\\\&\Rightarrow&8\times MN=80-10x\\\\&\Rightarrow&MN=\dfrac{80-10x}{8}\\\\&\Rightarrow&MN=\dfrac{40-5x}{2}\\\\&\Rightarrow&MN=\dfrac{40}{2}-\dfrac{5x}{2}\\\\&\Rightarrow&MN=20-\dfrac{5x}{2}\end{array}$

 

D'où, $\boxed{MN=20-\dfrac{5x}{2}}$

 

$-\ $ Expression de $MP$ en fonction de $x$

 

En effet, comme les droites $(MP)\ $ et $\ (BD)$ sont parallèles alors, les triangles $AMP\ $ et $\ ABD$ sont en position de Thalès.

 

Ainsi, en appliquant le théorème de Thalès, on obtient : $$\dfrac{MP}{BD}=\dfrac{AM}{AB}$$

 

Or, on sait que : $ABCD$ est un rectangle donc, les diagonales $[AC]\ $ et $\ [BD]$ ont même longueur.

 

Ainsi, $BD=AC=10\,cm$

 

Par suite, en remplaçant $AM\;,\ AB\ $ et $\ BD$ par leur valeur, on trouve :

 

$\begin{array}{rcl}\dfrac{MN}{BD}=\dfrac{AM}{AB}&\Rightarrow&\dfrac{MP}{10}=\dfrac{x}{8}\\\\&\Rightarrow&8\times MP=10\times x\\\\&\Rightarrow&MP=\dfrac{10x}{8}\\\\&\Rightarrow&MP=\dfrac{5x}{2}\end{array}$

 

D'où, $\boxed{MP=\dfrac{5x}{2}}$

 

2) Montrons que $MN+MP$ est indépendant de $x.$

 

En calculant l'expression $MN+MP$, on a :

 

$\begin{array}{rcl} MN+MP&=&20-\dfrac{5x}{2}+\dfrac{5x}{2}\\\\&=&20+\dfrac{5x-5x}{2}\\\\&=&20\end{array}$

 

Donc, $\boxed{MN+MP=20}$

 

On constate alors que l'expression $MN+MP$ donne un résultat qui ne dépend pas de $x.$

 

Par conséquent, on peut dire que $MN+MP$ est indépendant de $x.$

 

3) Déterminons les valeurs de $x$ pour lesquelles $MN=MP.$

 

En effet, on a :

 

$\begin{array}{rcl} MN=MP&\Leftrightarrow&20-\dfrac{5x}{2}=\dfrac{5x}{2}\\\\&\Leftrightarrow&-\dfrac{5x}{2}-\dfrac{5x}{2}=-20\\\\&\Leftrightarrow&\dfrac{-5x-5x}{2}=-20\\\\&\Leftrightarrow&\dfrac{-10x}{2}=-20\\\\&\Leftrightarrow&-5x=-20\\\\&\Leftrightarrow&x=\dfrac{-20}{-5}\\\\&\Leftrightarrow&x=4\end{array}$

 

D'où, $\boxed{x=4}$

 

Ainsi, lorsque $x$ est égal à $4$, les longueurs $MN\ $ et $\ MP$ sont égales.