Corrigé Exercice 18 : Distances - 4e
Classe:
Quatrième
Exercice 18
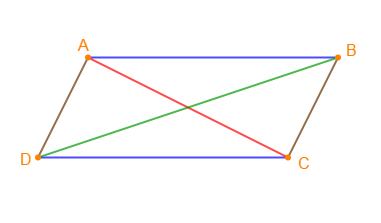
Soit $ABCD$ un parallélogramme.
Démontrons que :
Considérons le triangle $ABC.$
En appliquant l'inégalité triangulaire sur ce triangle $ABC$, on obtient :
Par ailleurs, en appliquant l'inégalité triangulaire sur le triangle $BCD$, on obtient :
Mais comme $ABCD$ est un parallélogramme alors, on a :
Ainsi, en remplaçant $DC$ par $AB$ dans l'inégalité $2$, on obtient :
Autre méthode :
On peut aussi appliquer l'inégalité triangulaire sur le triangle $ABD.$
Ce qui donne :
Or, $AD=BC$ car $ABCD$ est un parallélogramme. Donc, en remplaçant $AD$ par $BC$, on obtient :
Ajouter un commentaire