Corrigé Exercice 18 : Symétrie centrale 5e

 

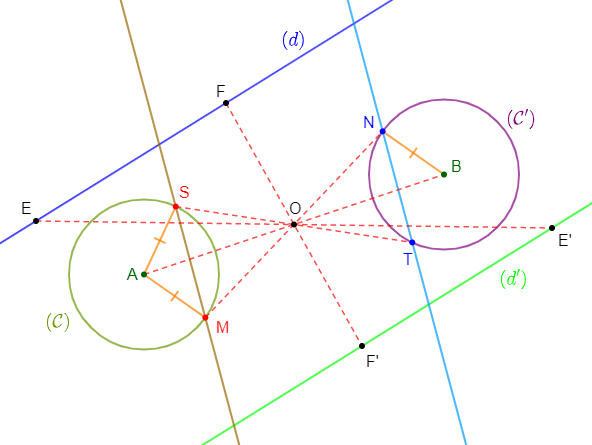
1) Reproduisons la figure puis, plaçons les points $T\;,\ B\ $ et $\ N$ symétriques respectifs des points $S\;,\ A\ $ et $\ M$ par rapport à $O.$

 

2) Construisons le symétrique $(\mathcal{C}')$ du cercle $(\mathcal{C})$ par rapport à $O.$

 

On a : $B$ est le symétrique du centre $A$ du cercle $(\mathcal{C})$ par rapport à $O$ donc, $B$ est le centre du cercle $(\mathcal{C}').$

 

On a aussi : $S\ $ et $\ M$ deux points de $(\mathcal{C})$ et $T\ $ et $\ N$ leurs symétriques respectifs par rapport à $O.$

 

Alors, le symétrique $(\mathcal{C}')$ du cercle $(\mathcal{C})$ par rapport à $O$ est le cercle de centre $B$ et passant par les points $T\ $ et $\ N.$

 

3) Construisons le symétrique $(d')$ de la droite $(d)$ par rapport à $O.$

 

Pour cela, on choisit deux points $E\ $ et $\ F$ appartenant à la droite $(d)$ puis, on construit leurs symétriques respectifs $E'\ $ et $\ F'$ par rapport à $O.$

 

Ensuite, on trace la droite passant par les points $E'\ $ et $\ F'$ ; c'est la droite $(d').$

 

a) Justifions que $AM=BN.$

 

On a : $B$ symétrique de $A$ par rapport à $O\ $ et $\ N$ symétrique de $M$ par rapport à $O$ donc, $[BN]$ est le symétrique du segment $[AM]$ par rapport à $O.$

 

Or, on sait que : le symétrique d'un segment par rapport à un point est un segment de même longueur.

 

Ce qui justifie que : $AM=BN.$

 

b) On a aussi : $SA=BN$

 

Justifions.

 

On a : $SA$ un rayon du cercle $(\mathcal{C})\ $ et $\ BN$ un rayon du cercle $(\mathcal{C}').$

 

Or, on sait que : le symétrique d'un cercle par rapport à un point est un cercle de même rayon.

 

Comme $(\mathcal{C}')$ est le symétrique de $(\mathcal{C})$ par rapport à $O$ alors, ces deux cercles ont même rayon.

 

D'où, $SA=BN$

 

c) Les droites $(SM)\ $ et $\ (TN)$ sont parallèles. Les droites $(d)\ $ et $\ (d')$ sont parallèles.

 

Justifions nos réponses.

 

On a : $T$ symétrique de $S$ par rapport à $O\ $ et $\ N$ symétrique de $M$ par rapport à $O$ donc, $(TN)$ est le symétrique de la droite $(SM)$ par rapport à $O.$

 

Or, on sait que : le symétrique d'une droite par rapport à un point est une droite qui lui est parallèle.

 

Par conséquent, les droites $(SM)\ $ et $\ (TN)$ sont parallèles.

 

Aussi, comme $(d')$ est le symétrique $(d)$ par rapport à $O$ alors, les droites $(d)\ $ et $\ (d')$ sont parallèles.