Corrigé Exercice 2 : Symétrie centrale 5e
Classe:
Cinquième
Exercice 2
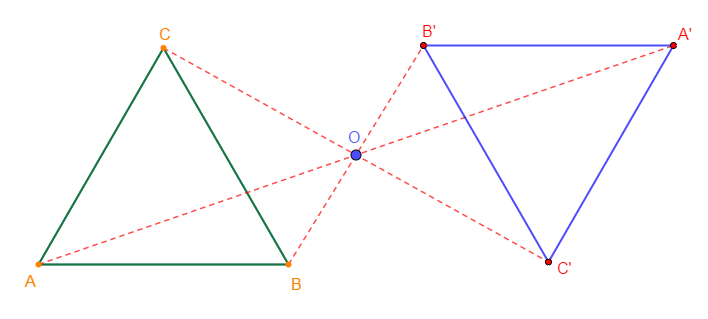
1) Traçons un triangle équilatéral $ABC$ tel que $AB=5\;cm.$
2) Construisons un point $O$ extérieur du triangle de $ABC.$
3) Construisons les points $A'\;,\ B'\ $ et $\ C'$ symétriques de $ABC$ par rapport à $O.$
4) $A'B'C'$ un triangle équilatéral tel que $A'B'=5\;cm.$
Justifions la réponse par une propriété du cours.
On a : $S_{O}[A]=A'\;,\ S_{O}[B]=B'\ $ et $\ S_{O}[C]=C'$
Donc, $S_{O}(ABC)=A'B'C'$
Par suite, $A'B'C'$ est le symétrique du triangle $ABC$ par rapport à $O.$
Or, d'après une propriété du cours, le symétrique d'un triangle est un triangle de même nature.
Par conséquent, $A'B'C'$ est un triangle équilatéral tel que $A'B'=5\;cm.$

Ajouter un commentaire