Corrigé Exercice 2 : Théorème de Thalès - 3e

 

Dans chacun des cas suivants, $E\;,\ A\;,\ C$ sont trois points alignés d'une part, et $E\;,\ B\;,\ D$ trois points alignés d'autre part, dans le même ordre.

 

Alors, d'après la réciproque du théorème de Thalès, si on a : $\dfrac{EA}{EC}=\dfrac{EB}{ED}$, on dira que les droites $(AB)\ $ et $\ (CD)$ sont parallèles.

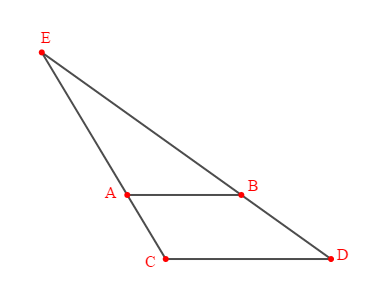
Dans le 1er cas on donne : $EA=\dfrac{1}{2}\;;\   EC=\dfrac{2}{3}\;;\ EB=3\;;\  ED=4$

 

Calculons alors les rapports $\dfrac{EA}{EC}\;,\ \dfrac{EB}{ED}$

 

On a : $\dfrac{EA}{EC}=\dfrac{\dfrac{1}{2}}{\dfrac{2}{3}}=\dfrac{3}{4}\;,\quad\text{et }\  \dfrac{EB}{ED}=\dfrac{3}{4}$

 

Par suite, $\dfrac{EA}{EC}=\dfrac{EB}{ED}$

 

Ainsi, les droites $(AB)\ $ et $\ (CD)$ sont parallèles.

 

Dans le 2ème cas on donne : $EA=2\;;\ EC=3.2\;;\ EB=4\;;\ ED=6$

 

Le calcul des rapports $\dfrac{EA}{EC}\;,\ \dfrac{EB}{ED}$ donne : $\dfrac{EA}{EC}=\dfrac{2}{3.2}=\dfrac{2}{3.2}\;,\quad\text{et }\  \dfrac{EB}{ED}=\dfrac{4}{6}=\dfrac{2}{3}$

 

Ce qui montre que les rapports $\dfrac{EA}{EC}\ $ et $\ \dfrac{EB}{ED}$ sont différents ; $\ \left(\dfrac{2}{3.2}\neq\dfrac{2}{3}\right)$

 

Or, pour que les droites $(AB)\ $ et $\ (CD)$ soient parallèles, il faut avoir $\dfrac{EA}{EC}=\dfrac{EB}{ED}$, d'après la réciproque du théorème de Thalès.

 

Par conséquent, les droites $(AB)\ $ et $\ (CD)$ ne sont pas parallèles, pour ce deuxième cas.