Corrigé Exercice 21 : Distances - 4e

 

$ABC$ est un triangle isocèle en $A.$

 

$H$ est le pied de la médiane issue de $A.$

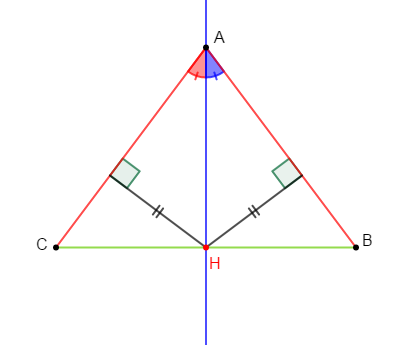
Démontrons que le point $H$ est équidistant des côtés $[AB]\ $ et $\ [AC].$

 

Comme $ABC$ est un triangle isocèle en $A$ alors, la médiane $(AH)$ issue de $A$ est aussi bissectrice de l'angle $\widehat{A}.$

 

Ainsi, $H$ appartient à la bissectrice de l'angle $\widehat{A}$ dont les côtés sont $[AB]\ $ et $\ [AC].$

 

Or, on sait que dans un triangle, si un point appartient à la bissectrice d'un angle alors, il est équidistant des deux côtés de l'angle.

 

Par conséquent, le point $H$ est équidistant des côtés $[AB]\ $ et $\ [AC]$ de l'angle $\widehat{A}.$