Corrigé Exercice 22 : Distances - 4e

 

1) Traçons un segment $[AB]$, puis traçons sa médiatrice $(\mathcal{D}).$

 

2) Marquons un point $M$ dans le demi-plan $(P_{B})$, de frontière $(\mathcal{D})$, contenant le point $B$, puis traçons le segment $[MA]$ qui coupe $(\mathcal{D})$ en $I.$

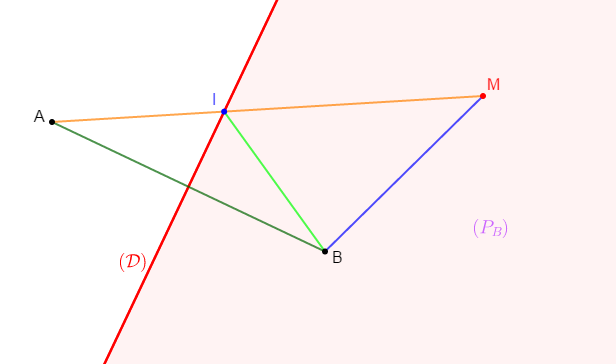
3) En considérant le triangle $MIB$, montrons que $MI+IB>MB.$

 

En appliquant l'inégalité triangulaire sur le triangle $MIB$, on obtient : $MB<MI+IB$

 

Ce qui peut encore s'écrire :

$$MI+IB>MB$$

4) Montrons que $IB=IA$ et déduisons-en que $MA>MB.$

 

Comme $(\mathcal{D})$ est médiatrice de $[AB]$ alors, pour tout point $M$ appartenant à la droite $(\mathcal{D})$, on a :

$$MA=MB$$

Or, le point $I$ appartient à $(\mathcal{D}).$

 

Donc, $I$ vérifie : $IA=IB$

 

D'où, on a :

$$IB=IA$$

Par ailleurs, d'après la question 3), on a : $MI+IB>MB$

 

Or, nous venons juste de montrer que $IB=IA.$

 

Donc, en remplaçant $IB$ par $IA$, on obtient :

$$MI+IA>MB$$

De plus, on constate que $I\in[AM].$ Donc, $MI+IA=MA$

 

Par suite, en remplaçant $MI+IA$ par $MA$, on obtient :

$$MA>MB$$