Corrigé Exercice 24 : Symétrie centrale 5e

 

On donne un segment $[AM].$

 

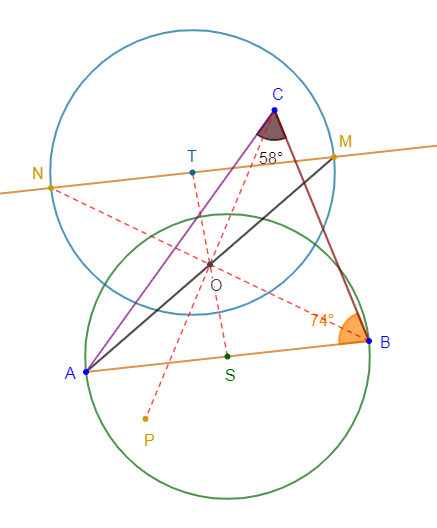
1) Construisons le triangle $ABC$ tel que $\widehat{ABC}=74^{\circ}\ $ et $\ \widehat{ACB}=58^{\circ}\;,\ B\ $ et $\ C$ distincts de $M.$

 

2) Plaçons le point $O$ milieu du segment $[AM].$

 

3) Construisons les points $N\ $ et $\ P$ symétriques respectifs des points $B\ $ et $\ C$ par rapport au point $O.$

 

4) Justifions que $M$ est le symétrique du point $A$ par rapport à $O.$

 

Comme $O$ est le  milieu du segment $[AM]$ alors, les points $A\ $ et $\ M$ sont symétriques par rapport à $O.$

 

D'où, $M$ est le symétrique du point $A$ par rapport à $O.$

 

5) Les droites $(AB)\ $ et $\ (NM)$ sont parallèles.

 

Justifions notre réponse.

 

On a :

 

$M$ symétrique de $A$ par rapport à $O$

 

$N$ symétrique de $B$ par rapport à $O$

 

Donc, $(MN)$ est le symétrique de $(AB)$ par rapport au point $O.$

 

Or, on sait que : le symétrique d'une droite par rapport à un point est une droite qui lui est parallèle.

 

Par conséquent, les droites $(AB)\ $ et $\ (NM)$ sont parallèles.

 

6) Les points $A\;,\ P\ $ et $\ N$ ne sont pas alignés.

 

Justifions notre réponse.

 

On sait que les symétriques de points non alignés sont des points non alignés.

 

Or, on remarque que les points $M\;;\ C\ $ et $\ B$ ne sont pas alignés.

 

Par conséquent, leurs symétriques respectifs $A\;,\ P\ $ et $\ N$ ne sont pas alignés.

 

7) Construisons le cercle de diamètre $[AB]$ et appelle $S$ son centre puis, construisons le symétrique de ce cercle par rapport à $O.$

 

Pour construire le symétrique de ce cercle, on construit d'abord le symétrique $T$ du centre $S$ par rapport à $O$ puis, on trace le cercle de centre $T$ et de même rayon.

 

$[MN]$ est le diamètre du cercle de centre $T.$

 

On a :

 

$M$ symétrique de $A$ par rapport à $O$

 

$N$ symétrique de $B$ par rapport à $O$

 

Donc, $[MN]$ est le symétrique de $[AB]$ par rapport à $O.$

 

Comme $[AB]$ est diamètre du cercle de centre $S$ alors, $[MN]$ est diamètre du symétrique de ce cercle par rapport à $O.$

 

D'où, $[MN]$ est le diamètre du cercle de centre $T.$