Corrigé Exercice 25 : Symétrie centrale 5e

 

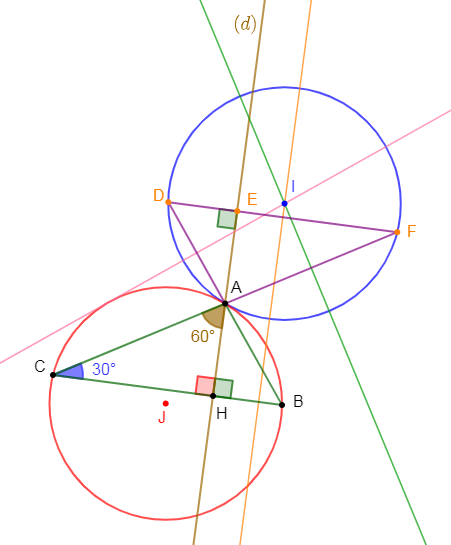
Soit $ABC$ un triangle tel que $\widehat{BCA}=30^{\circ}\ $ et $\ (d)$ la hauteur passant par $A$ ; la droite $(d)$ coupe la droite $(BC)$ en $H.$

 

1) La mesure de l'angle $\widehat{HAC}$ est égale à $60^{\circ}$

 

En effet, comme $H$ est le pied de la hauteur issue de $A$ alors, le triangle $AHC$ est rectangle en $H.$

 

Or, on sait que : dans un triangle rectangle, les angles aigus sont complémentaires.

 

Ce qui signifie que : $\widehat{HAC}+\widehat{BCA}=90^{\circ}$

 

Ce qui donne : $\widehat{HAC}=90^{\circ}-\widehat{BCA}$

 

En remplaçant $\widehat{BCA}$ par sa valeur, on obtient :

 

$\begin{array}{rcl}\widehat{HAC}&=&90^{\circ}-\widehat{BCA}\\\\&=&90^{\circ}-30^{\circ}\\\\&=&60^{\circ}\end{array}$

 

D'où, $\boxed{\widehat{HAC}=60^{\circ}}$

 

2) Soit les points $D\;,\ E\ $ et $\ F$ symétriques respectifs des points $B\;,\ H\ $ et $\ C$ par rapport au point $A.$

 

a) Justifions que les points $D\;,\ E\;,\ F$ sont alignés.

 

On a : $H\in[BC]$ donc, les points $B\;,\ H\ $ et $\ C$ sont alignés.

 

On sait que : les symétriques de points alignés par rapport à un point sont des points alignés.

 

Or, les points $D\;,\ E\ $ et $\ F$ sont symétriques respectifs des points $B\;,\ H\ $ et $\ C$ par rapport au point $A.$

 

Donc, ils sont alignés.

 

b) La mesure de l'angle $\widehat{AED}$ est égale à $90^{\circ}$

 

Justifions notre réponse.

 

On a :

 

$E$ est le symétrique de $H$ par rapport à $A$

 

$D$ est le symétrique de $B$ par rapport à $A$

 

$A$ est le symétrique de $A$ par rapport à $A$

 

Donc, l'angle $\widehat{AED}$ est le symétrique de l'angle $\widehat{AHB}$ par rapport au point $A.$

 

Par conséquent, ces deux angles sont de même mesure.

 

D'où, $\boxed{\widehat{AED}=90^{\circ}}$

 

c) Construisons le cercle circonscrit au triangle $AFD.$

 

Pour cela, on trace les trois médiatrices du triangle $AFD$ et leur point de rencontre $I$ représente le centre du cercle circonscrit à ce triangle.

 

d) Construisons le plus simplement possible le cercle circonscrit au triangle $ABC.$

 

On sait que les triangles $ABC\ $ et $\ AFD$ sont symétriques par rapport au point $A.$

 

Donc, le cercle circonscrit au triangle $ABC$ est symétrique du cercle circonscrit au triangle $AFD$ par rapport à $A.$

 

Alors, on construit le symétrique $J$ du centre $I$ par rapport à $A$ puis, on trace le cercle de centre $J$ et passant par les sommets $A\;;\ B\ $ et $\ C.$ C'est le cercle circonscrit au triangle $ABC.$