Corrigé Exercice 25 : Théorème de Thalès - 3e

 

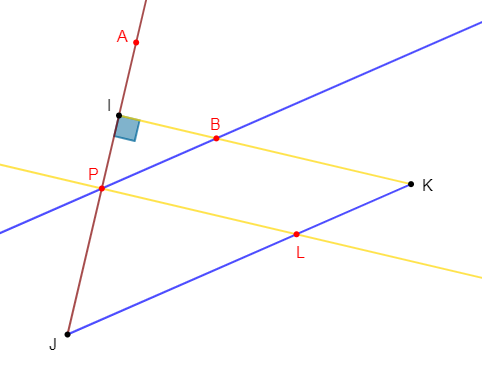
1) Construisons un triangle $IJK$ rectangle en $I$ tel que : $IJ=4.5\;cm\ $ et $\ IK=6\;cm.$

 

2) Calculons $JK.$

 

Comme $IJK$ est un triangle rectangle en $I$ alors, en appliquant le théorème de Pythagore, on a :

$$JK^{2}=IJ^{2}+IK^{2}$$

Ainsi,

 

$\begin{array}{rcl} JK^{2}=IJ^{2}+IK^{2}&\Rightarrow&JK=\sqrt{IJ^{2}+IK^{2}}\\\\&\Rightarrow&JK=\sqrt{(4.5)^{2}+6^{2}}\\ \\&\Rightarrow&JK=\sqrt{20.25+36}\\ \\&\Rightarrow&JK=\sqrt{56.25}\\\\&\Rightarrow&JK=7.5\end{array}$

 

D'où, $\boxed{JK=7.5\;cm}$

 

3) Plaçons le point $P\in[IJ]$ tel que $JP=3\;cm$, puis traçons la parallèle à $(IK)$ passant par $P$ qui coupe $(JK)$ en $L.$

 

4) Calculons les distances $JL\ $ et $\ PL.$

 

$-\ $ Calcul de $JL$

 

Les droites $(IK)\ $ et $\ (PL)$ étant parallèles alors, les triangles $IJK\ $ et $\ JPL$ sont en position de Thalès.

 

Ainsi, en appliquant le théorème de Thalès, on a :

$$\dfrac{JL}{JK}=\dfrac{JP}{IJ}$$

Alors, en remplaçant $JK\;,\ JP\ $ et $\ IJ$ par leur valeur, on obtient :

 

$\begin{array}{rcl}\dfrac{JL}{7.5}=\dfrac{3}{4.5}&\Leftrightarrow&4.5\times JL=3\times 7.5\\\\&\Leftrightarrow&JL=\dfrac{22.5}{4.5}\\\\&\Leftrightarrow&JL=5\end{array}$

 

D'où, $\boxed{JL=5\;cm}$

 

$-\ $ Calcul de $PL$

 

En appliquant encore le théorème de Thalès, on a :

$$\dfrac{PL}{IK}=\dfrac{JP}{IJ}$$

Alors, en remplaçant $IK\;,\ JP\ $ et $\ IJ$ par leur valeur, on obtient :

 

$\begin{array}{rcl}\dfrac{PL}{6}=\dfrac{3}{4.5}&\Leftrightarrow&4.5\times PL=3\times 6\\\\&\Leftrightarrow&PL=\dfrac{18}{4.5}\\\\&\Leftrightarrow&PL=4\end{array}$

 

D'où, $\boxed{PL=4\;cm}$

 

5) Soit $A_{1}$ l'aire du triangle $IJK$ et $A_{2}$ celle du triangle $JPL.$

 

Montrons que $\dfrac{A_{2}}{A_{1}}=\left(\dfrac{JI}{JP}\right)^{2}.$

 

En effet, le triangle $IJK$ étant un agrandissement du triangle $JPL$ alors, le coefficient d'agrandissement des longueurs peut être donné par :

$$m=\dfrac{JI}{JP}$$

Par suite, le coefficient d'agrandissement des aires est :

$$m^{2}=\left(\dfrac{JI}{JP}\right)^{2}$$

Ainsi, $A_{2}=m^{2}\times A_{1}$

 

Ce qui donne : $\dfrac{A_{2}}{A_{1}}=m^{2}=\left(\dfrac{JI}{JP}\right)^{2}.$

 

D'où, $\boxed{\dfrac{A_{2}}{A_{1}}=\left(\dfrac{JI}{JP}\right)^{2}}$

 

6) Construisons sur $[JI)$, le point $A$ tel que $JA=6\;cm$ puis sur $[KI)$ le point $B$ tel que $IB=2\;cm\ $ et $\ B\in[KI].$

 

7) Démontrons que les droites $(PB)\ $ et $\ (KJ)$ sont parallèles.

 

En effet, $I\;,\ P\;,\ J$ sont trois points alignés d'une part, et $I\;,\ B\;,\ K$ sont trois points alignés d'autre part, dans le même ordre.

 

En calculant les rapports $\dfrac{IP}{IJ}\ $ et $\ \dfrac{IB}{IK}$, on a :

 

$\dfrac{IP}{IJ}=\dfrac{IJ-JP}{IJ}=\dfrac{4.5-3}{4.5}=\dfrac{1.5}{4.5}=\dfrac{1}{3}$

 

$\dfrac{IB}{IK}=\dfrac{2}{6}=\dfrac{1}{3}$

 

On constate alors que : $\dfrac{IP}{IJ}=\dfrac{IB}{IK}$

 

Par conséquent, d'après la réciproque du théorème de Thalès, les droites $(PB)\ $ et $\ (KJ)$ sont parallèles.