Corrigé Exercice 27 : Symétrie centrale 5e

 

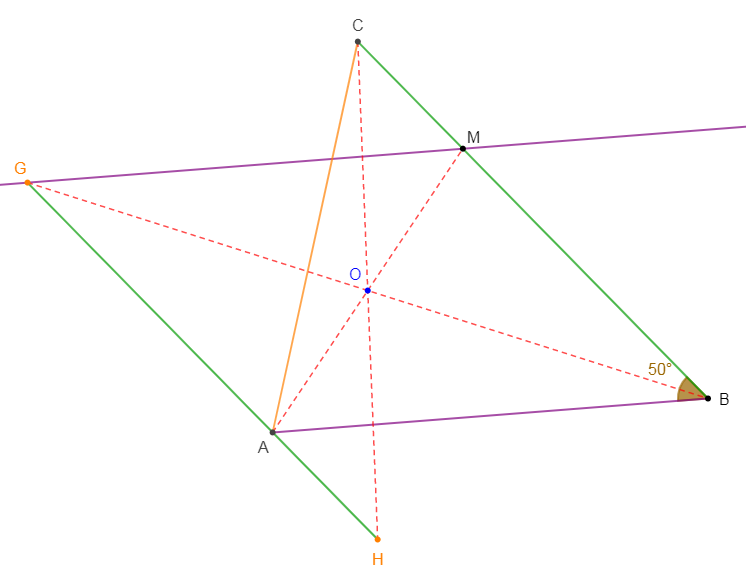
1) Traçons le triangle $ABC$ tel que $AC=8\;cm\;;\ \widehat{ABC}=50^{\circ}\ $ et $\ BC=10\;cm$ et plaçons le point $M$ du segment $[BC]$ tel que $CM=3\;cm.\ O$ est le milieu du segment $[AM].$

 

2) Construisons les points $G\ $ et $\ H$ symétriques respectifs des points $B\ $ et $\ C$ par rapport à $O.$

 

3) Démontrons que les longueurs $GH\ $ et $\ BC$ sont égales.

 

On a :

 

$G$ symétrique de $B$ par rapport à $O.$

 

$H$ symétrique de $C$ par rapport à $O.$

 

Donc, le segment $[GH]$ est le symétrique du segment $[BC]$ par rapport au point $O.$

 

Or, on sait que : le symétrique d'un segment par rapport à un point est un segment de même longueur.

 

D'où, les longueurs $GH\ $ et $\ BC$ sont égales.

 

4) Démontrons que les droites $(AB)\ $ et $\ (MG)$ sont parallèles.

 

Comme $O$ est milieu de $[AM]$ alors, $M$ est le symétrique de $A$ par rapport à $O.$

 

On a aussi, $G$ symétrique de $B$ par rapport à $O.$

 

Donc, la droite $(MG)$ est le symétrique de la droite $(AB)$ par rapport à $O.$

 

Or, le symétrique d'une droite par rapport à un point est une droite qui lui est parallèle.

 

Ainsi, les droites $(AB)\ $ et $\ (MG)$ sont parallèles.

 

5) Démontrons que les points $A\;,\ G\ $ et $\ H$ sont alignés.

 

On a : les points $A\;,\ G\ $ et $\ H$ sont les symétriques respectifs des points $M\;;\ B\ $ et $\ C$ par rapport à $O.$

 

Or, $M\;;\ B\ $ et $\ C$ sont alignés et les symétriques de points alignés sont des points alignés.

 

Donc, les points $A\;,\ G\ $ et $\ H$ sont alignés.