Corrigé Exercice 28 : Symétrie centrale 5e

 

On considère un quadrilatère $ABCD$ surmonté d'un demi-cercle de diamètre $[AB].$

 

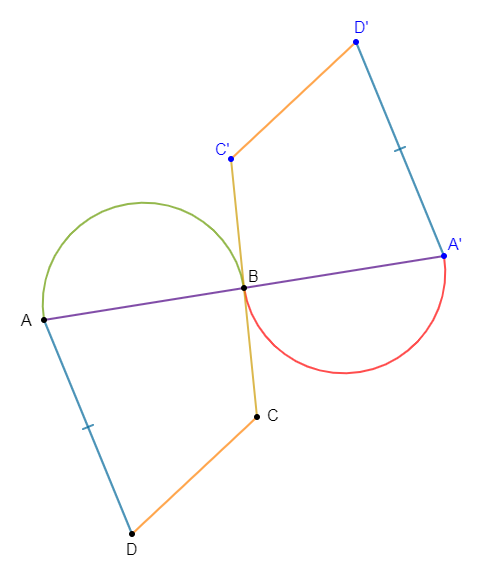
1) Faisons une figure puis, construisons son symétrique par rapport à $B.$ On appellera $A'\;,\ C'\ $ et $\ D'$ les symétriques respectifs des points $A\;,\ C\ $ et $\ D$ par rapport à $B.$

 

2) $[AD]\ $ et $\ [A'D']$ sont deux segments de même longueur.

 

On a :

 

$A'$ symétrique de $A$ par rapport à $B.$

 

$D'$ symétrique de $D$ par rapport à $B.$

 

Donc, le segment $[A'D']$ est le symétrique du segment $[AD]$ par rapport au point $B.$

 

Comme le symétrique d'un segment par rapport à un point est un segment de même longueur alors, $[AD]\ $ et $\ [A'D']$ ont même longueur.

 

Remarque : on peut encore trouver d'autres segments qui sont de même longueur.

 

3) Démontrons que les droites $(AD)\ $ et $\ (A'D')$ sont parallèles.

 

On a :

 

$A'$ symétrique de $A$ par rapport à $B.$

 

$D'$ symétrique de $D$ par rapport à $B.$

 

Donc, la droite $(A'D')$ est le symétrique de la droite $(AD)$ par rapport au point $B.$

 

Or, le symétrique d'une droite par rapport à un point est une droite qui lui est parallèle.

 

D'où, les droites $(AD)\ $ et $\ (A'D')$ sont parallèles.