Corrigé Exercice 29 : Distances - 4e
Classe:
Quatrième
Exercice 29
$EGH$ est un triangle rectangle en $E.$
$(\mathcal{C})$ est le cercle de centre $G$ et de rayon $EG.$
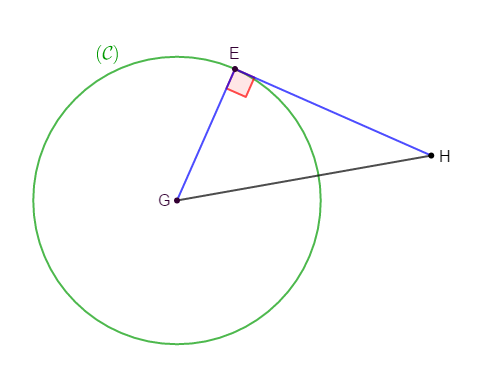
Démontrons que $(\mathcal{C})\ $ et $\ (EH)$ sont tangents.
Comme $EGH$ est un triangle rectangle en $E$ alors, les droites $(EG)\ $ et $\ (EH)$ sont perpendiculaires en $H.$
Par suite, le point $E$ est le pied de la perpendiculaire passant par $G.$
Ainsi, $EG$ est la distance de $G$ à la droite $(EH).$
Par ailleurs, on sait que $(\mathcal{C})$ est le cercle de centre $G$ et de rayon $EG.$
Donc, le rayon du cercle $(\mathcal{C})$ est égal à la distance du centre $G$ de ce cercle à la droite $(EH).$
D'où, $(\mathcal{C})\ $ et $\ (EH)$ sont tangents.

Ajouter un commentaire