Corrigé Exercice 3 : Introduction à la géométrie - Le plan et ses parties - 6e

Classe:

Sixième

1) Reproduisons la figure

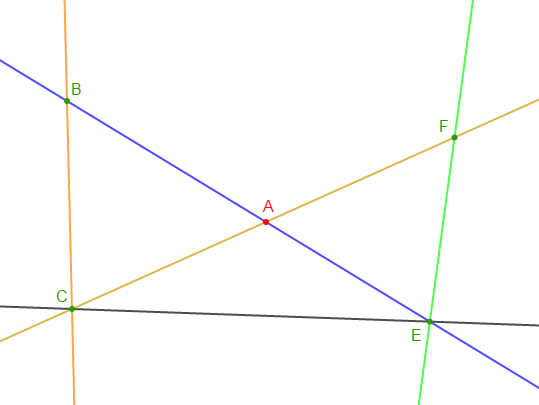
2) Complétons les pointillés par

$\in$ ou

$\notin .$

$A\in(BE)\;;\quad A\notin(CE)\;;\quad B\notin(AC)\;;\quad B\in(AE)$

La droite

$(BE)$ passe par le pont

$A$ donc,

$A\in(BE)$

Le point

$A$ n'est pas sur la droite

$(CE)$ donc,

$A\notin(CE)$

Comme la droite

$(AC)$ ne passe pas par

$B$ alors,

$B\notin(AC)$

La droite

$(AE)$ passe par le pont

$B$ donc, on peut dire

$B\in(AE)$

3) On constate que les droites

$(BE)\$ et

$\ (CF)$ se coupent au point

$A.$

Donc, on peut dire que

$A$ est le point de rencontre ou encore le point d'intersection des droites

$(BE)\$ et

$\ (CF)$

4) Traçons les droites

$(BC)\$ et

$\ (EF).$

Auteur:

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.