Corrigé Exercice 3 : Symétrie centrale 5e

Classe:

Cinquième

Soit

$ABCD$ un carré de côté

$4\;cm.$

1) Construisons le point

$O$ centre de symétrique de

$ABCD.$

C'est le point de rencontre des deux diagonales.

2) Construisons les points

$E\;;\ F$ et

$G$ symétriques respectifs des points

$B\;;\ C\$ et

$\ D$ par rapport à

$A.$

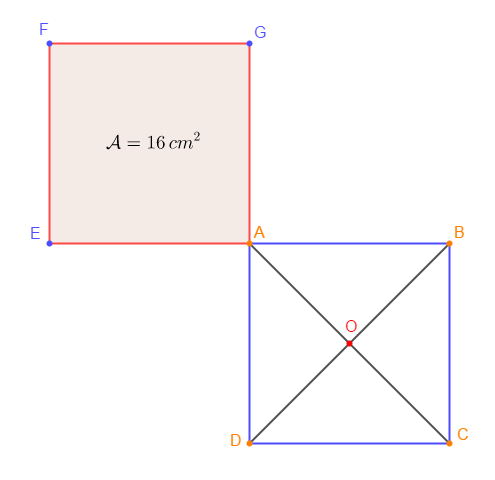
3) a) On a :

$S_{A}[A]=A\;,\ S_{A}[B]=E\;,\ S_{A}[C]=F\$ et

$\ S_{A}[D]=G$

Donc,

$S_{A}(ABCD)=AEFG$

Par suite,

$AEFG$ est le symétrique du carré

$ABCD$ par rapport à

$A.$

b) En utilisant la figure complétons :

$S_{A}(A)=A\;;\ S_{A}(CD)=(FG)\;;\ S_{A}([AD))=([AG))$

4) Le symétrique d'un carré est un carré de même dimension.

Donc,

$AEFG$ est un carré de côté

$4\;cm.$

Son aire

$\mathcal{A}$ est donnée par :

$\begin{array}{rcl}\mathcal{A}&=&\text{côté}\times\text{côté}\\ \\&=&4\,cm\times 4\,cm\\ \\&=&16\,cm^{2}\end{array}$

Ainsi,

$\boxed{\mathcal{A}=16\,cm^{2}}$

Auteur:

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.