Corrigé Exercice 34 : Racine carrée 3e

 

Écrivons le plus simplement possible les expressions ci-dessous :
$$G=\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\sqrt{\dfrac{9}{4}}}}}}}$$
En calculant de la droite vers la gauche, on obtient :

$\begin{array}{rcl} G&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\sqrt{\dfrac{9}{4}}}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\times\dfrac{\sqrt{9}}{\sqrt{4}}}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-2\times\dfrac{3}{2}}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{103-3}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+\sqrt{100}}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{6+10}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times\sqrt{16}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{1}{25}\times 4}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{21}{25}+\dfrac{4}{25}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{\dfrac{25}{25}}}}\\\\&=&\sqrt{76-2\sqrt{37-\sqrt{1}}}\\\\&=&\sqrt{76-2\sqrt{37-1}}\\\\&=&\sqrt{76-2\sqrt{36}}\\\\&=&\sqrt{76-2\times 6}\\\\&=&\sqrt{76-12}\\\\&=&\sqrt{64}\\\\&=&8\end{array}$

D'où, $\boxed{G=8}$

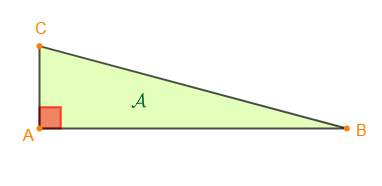
On donne un triangle $ABC$ rectangle en $A$ tel que $AC=\sqrt{3}-1\ $ et $\ BC=2\sqrt{2}.$

1) Calculons $AB^{2}$, déduisons-en que $AB=\sqrt{3}+1$ puis l'aire du triangle $ABC.$

Comme le triangle $ABC$ est rectangle en $A$ alors, d'après le théorème de Pythagore, on a :
$$AB^{2}+AC^{2}=BC^{2}$$
Ce qui entraine : $AB^{2}=BC^{2}-AC^{2}$

En remplaçant $AC^{2}\ $ et $\ BC^{2}$ par leur valeur, on obtient :

$\begin{array}{rcl} AB^{2}&=&BC^{2}-AC^{2}\\\\&=&(2\sqrt{2})^{2}-(\sqrt{3}-1)^{2}\\\\&=&(4\times 2)-\left((\sqrt{3})^{2}-2\times 1\times\sqrt{3}+(1)^{2}\right)\\\\&=&8-(3-2\sqrt{3}+1)\\\\&=&8-(4-2\sqrt{3})\\\\&=&8-4+2\sqrt{3}\\\\&=&4+2\sqrt{3}\end{array}$

Donc, $\boxed{AB^{2}=4+2\sqrt{3}}$

Déduisons-en que $AB=\sqrt{3}+1$

Comme $AB^{2}=4+2\sqrt{3}$ alors, on a : $\sqrt{AB^{2}}=\sqrt{4+2\sqrt{3}}$

Or, on sait que : $4+2\sqrt{3}=(\sqrt{3}+1)^{2}$

Donc, en remplaçant, on obtient : $\sqrt{AB^{2}}=\sqrt{(\sqrt{3}+1)^{2}}$

Ce qui donne : $|AB|=\left|\sqrt{3}+1\right|$

Par ailleurs, on sait que $AB$ est la longueur d'un côté du triangle donc, $AB$ est positive.

D'où, $|AB|=AB$

De plus, la somme de deux nombres positifs est un nombre positif donc, $\sqrt{3}+1>0$

Ainsi, $\left|\sqrt{3}+1\right|=\sqrt{3}+1$

Par conséquent, $\boxed{AB=\sqrt{3}+1}$

Calculons l'aire $\mathcal{A}$ de ce triangle.

On a :

$\begin{array}{rcl}\mathcal{A}&=&\dfrac{AB\times AC}{2}\\\\&=&\dfrac{(\sqrt{3}+1)\times(\sqrt{3}-1)}{2}\\\\&=&\dfrac{(\sqrt{3})^{2}-(1)^{2}}{2}\\\\&=&\dfrac{3-1}{2}\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$

Ainsi, $\boxed{\mathcal{A}=1}$

2) Calculons $\dfrac{1}{AC}$ sans radical au dénominateur.

Soit : $\dfrac{1}{AC}=\dfrac{1}{\sqrt{3}-1}$

Donc, rendons rationnel le dénominateur de $\dfrac{1}{\sqrt{3}-1}$

Comme $\sqrt{3}+1$ est l'expression conjuguée de $\sqrt{3}-1$ alors, on a :

$\begin{array}{rcl}\dfrac{1}{AC}&=&\dfrac{1}{\sqrt{3}-1}\\\\&=&\dfrac{1\times(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}\\\\&=&\dfrac{\sqrt{3}+1}{(\sqrt{3})^{2}-(1)^{2}}\\\\&=&\dfrac{\sqrt{3}+1}{3-1}\\\\&=&\dfrac{\sqrt{3}+1}{2}\end{array}$

Ainsi, $\boxed{\dfrac{1}{AC}=\dfrac{\sqrt{3}+1}{2}}$

Déduisons-en un encadrement de $\dfrac{1}{AC}$ d'amplitude $0.01$

On sait que : $1.73<\sqrt{3}<1.74$

Alors, ajoutons $1$ à chaque membre de l'inégalité.

On obtient :
$$1.73+1<\sqrt{3}+1<1.74+1$$
Ce qui donne : $2.73<\sqrt{3}+1<2.74$

Divisons ensuite chaque membre de cette dernière inégalité par le même nombre $2.$

On trouve alors :
$$\dfrac{2.73}{2}<\dfrac{\sqrt{3}+1}{2}<\dfrac{2.74}{2}$$
Ce qui est équivalent à : $1.36<\dfrac{\sqrt{3}+1}{2}<1.37$

D'où, un encadrement de $\dfrac{1}{AC}$ d'amplitude $0.01$ est donné par :
$$\boxed{1.36<\dfrac{1}{AC}<1.37}$$