Corrigé Exercice 35 : Racine carrée 3e

 

$ABCD\ $ et $\ CHIJ$ sont des carrés de côtés respectifs : $5\sqrt{3}-1\ $ et $\ \sqrt{27}.$ (Voir figure ci-dessous)
 

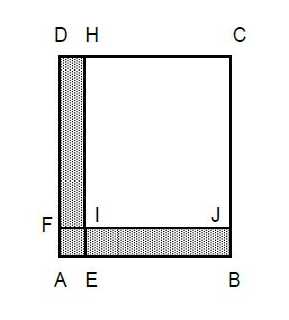
1) Calculons l'aire du carré $ABCD.$

L'aire $\mathcal{A}_{_{(ABCD)}}$ est donnée par :
$$\mathcal{A}_{_{(ABCD)}}=(\text{côté})^{2}$$
Comme son côté est de longueur $5\sqrt{3}-1$ alors, on a :

$\begin{array}{rcl} \mathcal{A}_{_{(ABCD)}}&=&(\text{côté})^{2}\\\\&=&(5\sqrt{3}-1)^{2}\\\\&=&(5\sqrt{3})^{2}-2\times 1\times 5\sqrt{3}+(1)^{2}\\\\&=&(25\times 3)-10\sqrt{3}+1\\\\&=&75-10\sqrt{3}+1\\\\&=&76-10\sqrt{3}\end{array}$

Ainsi, $\boxed{\mathcal{A}_{_{(ABCD)}}=76-10\sqrt{3}}$

2) Calculons l'aire du carré $CHIJ.$

L'aire $\mathcal{A}_{_{(CHIJ)}}$ est donnée par :
$$\mathcal{A}_{_{(ABCD)}}=(\text{côté})^{2}$$
Or, le côté de ce carré a pour longueur $\sqrt{27}$ donc, on a :

$\begin{array}{rcl} \mathcal{A}_{_{(CHIJ)}}&=&(\text{côté})^{2}\\\\&=&(\sqrt{27})^{2}\\\\&=&27\end{array}$

D'où, $\boxed{\mathcal{A}_{_{(CHIJ)}}=27}$

3) Calculons la longueur $AE.$

On a : $AE=AB-EB$

En observant la figure, on remarque que $EB=IJ=\sqrt{27}$

De plus, on sait que $AB=5\sqrt{3}-1$

Donc, en remplaçant $AB$ par $5\sqrt{3}-1\ $ et $\ EB$ par $\sqrt{27}$, on obtient :

$\begin{array}{rcl} AE&=&AB-EB\\\\&=&5\sqrt{3}-1-\sqrt{27}\\\\&=&5\sqrt{3}-1-\sqrt{9\times 3}\\\\&=&5\sqrt{3}-1-\sqrt{9}\times\sqrt{3}\\\\&=&5\sqrt{3}-1-3\sqrt{3}\\\\&=&2\sqrt{3}-1\end{array}$

Ainsi, $\boxed{AE=2\sqrt{3}-1}$

4) Calculons le périmètre du rectangle $CDFJ.$

Le périmètre $\mathcal{P}_{_{(CDFJ)}}$ du rectangle $CDFJ$ est donné par :
$$\mathcal{P}_{_{(CDFJ)}}=2\times(CD+CJ)$$
Comme $CD=5\sqrt{3}-1\ $ et $\ CJ=\sqrt{27}$ alors, on a :

$\begin{array}{rcl} \mathcal{P}_{_{(CDFJ)}}&=&2\times(CD+CJ)\\\\&=&2\times(5\sqrt{3}-1+\sqrt{27})\\\\&=&2\times(5\sqrt{3}-1+\sqrt{9\times 3})\\\\&=&2\times(5\sqrt{3}-1+\sqrt{9}\times\sqrt{3})\\\\&=&2\times(5\sqrt{3}-1+3\sqrt{3})\\\\&=&2\times(8\sqrt{3}-1)\\\\&=&16\sqrt{3}-2\end{array}$

D'où, $\boxed{\mathcal{P}_{_{(CDFJ)}}=16\sqrt{3}-2}$

5) Calculons l'aire de la surface coloriée.

En observant la figure, on remarque l'aire de la surface coloriée est égale à la différence entre l'aire du carré $ABCD$ et celle du carré $CHIJ.$

Ainsi, on a :

$\begin{array}{rcl} \mathcal{A}_{_{(\text{partie coloriée})}}&=&\mathcal{A}_{_{(ABCD)}}-\mathcal{A}_{_{(CHIJ)}}\\\\&=&76-10\sqrt{3}-27\\\\&=&49-10\sqrt{3}\end{array}$

D'où, $\boxed{\mathcal{A}_{_{(\text{partie coloriée})}}=49-10\sqrt{3}}$