Corrigé Exercice 4 : Théorème de Thalès - 3e

 

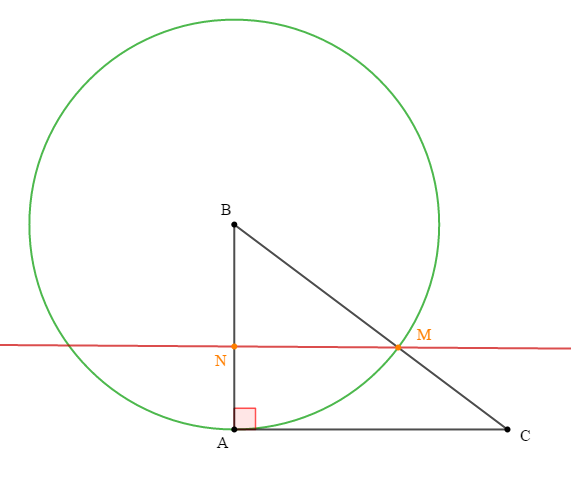
On considère le triangle $ABC$ rectangle en $A$ tel que $AB=6\ $ et $\ AC=8.$

 

Le cercle de centre $B$ et de rayon 6 coupe $[BC]$ en $M.$

 

Soit $N$ un point du segment $[AB]$ tel que $AN=2.4$

 

1) Calculons $BC$

 

Le triangle étant rectangle en $A$, on utilise le théorème de Pythagore pour calculer $BC.$

 

On a : 

 

$\begin{array}{rcl} BC^{2}=AB^{2}+AC^{2}&\Rightarrow&BC=\sqrt{AB^{2}+AC^{2}}\\\\&\Rightarrow&BC=\sqrt{36+64}\\\\&\Rightarrow&BC=\sqrt{100}\\\\&\Rightarrow&BC=10\end{array}$

 

D'où, $\boxed{BC=10}$

 

2) Démontrons que les droites $(MN)\ $ et $\ (AC)$ sont parallèles

 

Considérons $B\;,\ N\;,\ A$ trois points alignés d'une part, et $B\;,\ M\;,\ C$ trois points alignés d'autre part, dans le même ordre.

 

Calculons alors les rapports $\dfrac{BN}{AB}\quad\text{et}\quad\dfrac{BM}{BC}$

 

On a :

 

$\begin{array}{rcl}\dfrac{BN}{AB}&=&\dfrac{AB-AN}{AB}\quad\text{car, }\ BN=AB-AN\\ \\&=&\dfrac{6-2.4}{6}\\ \\&=&\dfrac{3.6}{6}\\ \\&=&0.6\end{array}$

 

D'où, $\dfrac{BN}{AB}=0.6$

 

Aussi, on sait que $M\in\;\mathcal{C}(B\;,\ 6)$ donc, $BM=6$

 

Par suite, $\dfrac{BM}{BC}=\dfrac{6}{10}=0.6$

 

Ce qui montre alors : $\dfrac{BN}{BA}=\dfrac{BM}{BC}$

 

Par conséquent, la réciproque du théorème de Thalès permet de conclure que les droites $(MN)\ $ et $\ (AC)$ sont parallèles.

 

Calculons $MN$

 

Les droites $(MN)\ $ et $\ (AC)$ étant parallèles alors, les triangles $BNM\ $ et $\ BAC$ sont en position de Thalès.

 

Ainsi, d'après le théorème de Thalès, on obtient : $$\dfrac{BN}{BA}=\dfrac{BM}{BC}=\dfrac{MN}{AC}$$

 

Par suite,

 

$\begin{array}{rcl}\dfrac{MN}{AC}=\dfrac{BM}{BC}&\Rightarrow&\dfrac{MN}{8}=\dfrac{6}{10}\\ \\&\Rightarrow&10\times MN=6\times 8\\ \\&\Rightarrow&MN=\dfrac{48}{10}\\ \\&\Rightarrow&MN=4.8\end{array}$

 

D'où, $\boxed{MN=4.8}$