Corrigé Exercice 5 : Racine carrée 3e

 

L'unité de longueur est le $hm.$ Les dimensions d'un champ rectangulaire sont : $2\sqrt{3}+2\ $ et $\ 2\sqrt{3}-2.$

 

Calculons : Le périmètre, l'aire ensuite, le diamètre du cercle circonscrit de ce champ rectangulaire.

 

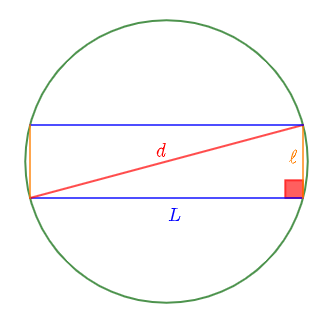
Soit $L$ la longueur du champ et $\ell$ sa largeur.

 

Alors, on a : $L=2\sqrt{3}+2\ $ et $\ \ell=2\sqrt{3}-2$

 

Ainsi, 

 

$-\ $ le périmètre $p$ du champ est donné par : 

 

$\begin{array}{rcl} p&=&2\times(L+\ell)\\\\&=&2\times((2\sqrt{3}+2)+(2\sqrt{3}-2))\\\\&=&2\times(2\sqrt{3}+2\sqrt{3}+2-2)\\\\&=&2\times(4\sqrt{3})\\\\&=&8\sqrt{3} \end{array}$

 

D'où, $\boxed{p=8\sqrt{3}\;hm}$

 

$-\ $ l'aire $\mathcal{A}$ du champ est donnée par : 

 

$\begin{array}{rcl}\mathcal{A}&=&L\times\ell\\\\&=&(2\sqrt{3}+2)\times(2\sqrt{3}-2)\\\\&=&(2\sqrt{3})^{2}-(2)^{2}\\\\&=&(4\times 3)-4\\\\&=&12-4\\\\&=&8\end{array}$

 

Donc, $\boxed{\mathcal{A}=8\;hm^{2}}$

 

$-\ $ le cercle circonscrit a pour diamètre l'une des diagonales du rectangle.

 

D'après le théorème de Pythagore, on a :

$$d^{2}=L^{2}+\ell^{2}$$

Ce qui entraine :

 

$\begin{array}{rcl} d&=&\sqrt{L^{2}+\ell^{2}}\\\\&=&\sqrt{(2\sqrt{3}+2)^{2}+(2\sqrt{3}-2)^{2}}\\\\&=&\sqrt{(2\sqrt{3})^{2}+2\times 2\times 2\sqrt{3}+2^{2}+(2\sqrt{3})^{2}-2\times 2\times 2\sqrt{3}+2^{2}}\\\\&=&\sqrt{12+8\sqrt{3}+4+12-8\sqrt{3}+4}\\\\&=&\sqrt{32}\\\\&=&\sqrt{16\times 2}\\\\&=&4\sqrt{2}\end{array}$

 

D'où, $\boxed{d=4\sqrt{2}\;hm}$