Corrigé Exercice 6 : Symétrie centrale 5e
Classe:
Cinquième
Exercice 6
1) Citons cinq lettres alphabet français admettant un centre de symétrique.
$$\mathbf{H}\;;\ \mathbf{O}\;;\ \mathbf{N}\;;\ \mathbf{X}\;;\ \mathbf{Z}$$
2) Citons trois figures géométriques admettant un centre de symétrique.
Le losange, le carré et le rectangle sont trois figures géométriques admettant un centre de symétrie.
Leur centre de symétrie est le point de rencontre de leurs diagonales.
Exemples :
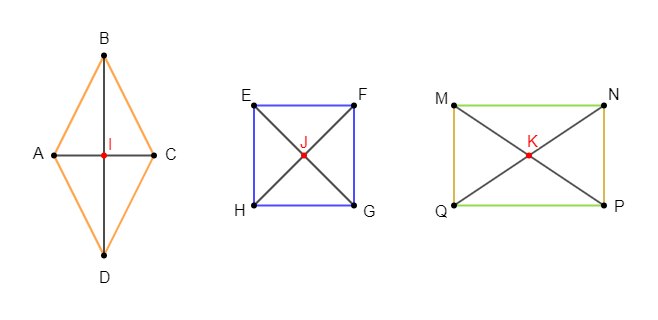
$I$ est le centre de symétrie du losange $ABCD.$
$J$ est le centre de symétrie du carré $EFGH.$
$K$ est le centre de symétrie du rectangle $MNPQ.$
3) Citons deux figures géométriques qui sont globalement invariant par la symétrie centrale.
Le cercle et le carré sont globalement invariant par la symétrie centrale de centre ; leur centre de symétrie.
Exemples :
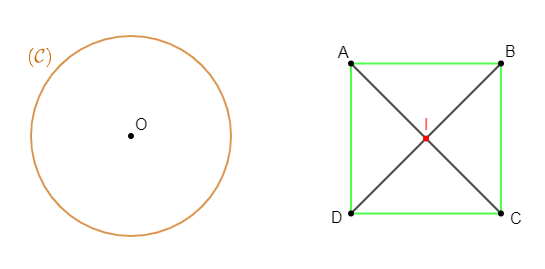
En effet, l'image du cercle $(\mathcal{C})$ par la symétrie centrale de centre $O$ est le même cercle $(\mathcal{C}).$
Donc, le cercle $(\mathcal{C})$ est globalement invariant par la symétrie centrale de centre $O.$
De la même manière, l'image du carré $ABCD$ par la symétrie centrale de centre $J$ est encore le même carré $ABCD.$
Ce qui signifie que le carré $ABCD$ est globalement invariant par la symétrie centrale de centre $I.$

Ajouter un commentaire