Corrigé Exercice 6 : Théorème de Thalès - 3e

 

On considère deux cercles $\mathcal{C}(O\;;\ 1.5)\ $ et $\ \mathcal{C}'(O'\;;\ 3)$ tangents extérieurement en $I.$

 

Soit $(\Delta)$ une droite tangente à $(\mathcal{C})\ $ et à $\ (\mathcal{C}')$ respectivement en $A\ $ et $\ B\;,\ (A\neq B).$

 

$(\Delta)$ coupe $(OO')$ en $P.$

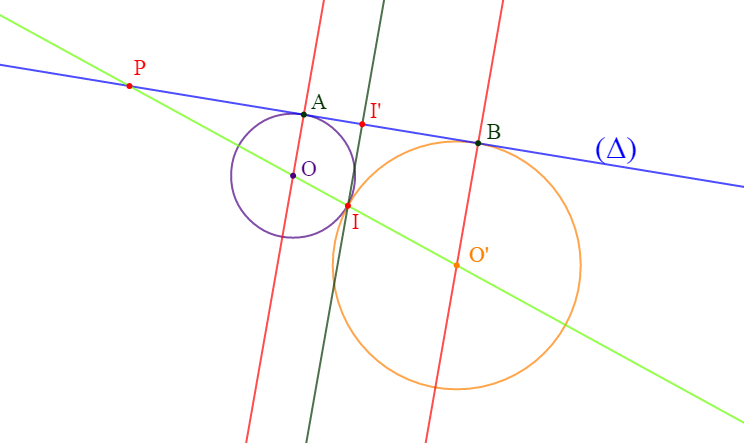
1) Démontrons que la droite $(OA)$ est parallèle à la droite $(O'B)$

 

On a :

 

$(\Delta)$ tangente à $(\mathcal{C})$ en $A$ alors, $(OA)$ est perpendiculaire à $(\Delta)$

 

aussi, $(\Delta)$ tangente à $(\mathcal{C}')$ au point $B$ donc, $(O'B)$ perpendiculaire à $(\Delta)$

 

Ainsi, $(OA)\ $ et $\ (O'B)$ sont deux droites perpendiculaires à une même droite $(\Delta).$

 

Par conséquent, $(OA)\ $ et $\ (O'B)$ sont parallèles.

 

2) a) On pose $PO=x$ ; exprimons $PO'$ en fonction de $x$ 

 

On a : 

 

$\begin{array}{rcl} PO'&=&PO+OO'\quad\text{or, }\ OO'=OI+IO'\\\\&=&PO+OI+IO'\\\\&=&x+1.5+3\\\\&=&x+4.5\end{array}$

 

D'où, $\boxed{PO'=x+4.5}$

 

Calculons $PO$

 

Comme $PO=x$ alors, calculer $PO$ revient à trouver la valeur de $x$

 

On a : $(PO')\ $ et $\ (PB)$ deux droites sécantes coupées par deux droites parallèles $(OA)\ $ et $\ (O'B)$ donc, les triangles $POA\ $ et $\ PO'B$ sont en position de Thalès.

 

Par suite, en appliquant le théorème de Thalès, on obtient : $$\dfrac{PO}{PO'}=\dfrac{OA}{O'B}=\dfrac{PA}{PB}$$

 

Ainsi,

 

$\begin{array}{rcl}\dfrac{PO}{PO'}=\dfrac{OA}{O'B}&\Rightarrow&\dfrac{x}{x+4.5}=\dfrac{1.5}{3}\\ \\&\Rightarrow&3x=1.5(x+4.5)\\ \\&\Rightarrow&3x-1.5x=1.5\times 4.5\\ \\&\Rightarrow&1.5x=6.75\\ \\&\Rightarrow&x=\dfrac{6.75}{1.5}\\ \\&\Rightarrow&x=4.5\end{array}$

 

D'où, $x=4.5\ $ or, $PO=x$

 

Par conséquent, $\boxed{PO=4.5}$

 

b) En déduisons la valeur exacte de $PA$

 

$PAO$ est un triangle rectangle en $A$ donc, d'après le théorème de Pythagore, on a : $$PO^{2}=PA^{2}+OA^{2}$$

 

Ainsi,

 

$\begin{array}{rcl} PO^{2}=PA^{2}+OA^{2}&\Rightarrow&PA^{2}=PO^{2}-OA^{2}\\ \\&\Rightarrow&PA=\sqrt{PO^{2}-OA^{2}}\\ \\&\Rightarrow&PA=\sqrt{20.25-2.25}\\ \\&\Rightarrow&PA=\sqrt{18}\\ \\&\Rightarrow&PA=3\sqrt{2}\end{array}$

 

D'où, $\boxed{PA=3\sqrt{2}}$

 

c) Démontrons que $PI=6$

 

On a : $PI=PO+OI\ $ or, $PO=4.5\ $ et $\ OI=1.5$

 

Par suite : $PI=4.5+1.5=6$

 

3) Soit $I'$ le point de $[AB]$ tel que $PI'=4\sqrt{2}.$ Démontrons que les droites $(OA)\ $ et $\ (II')$ sont parallèles. 

 

Considérons $P\;,\ A\;,\ I'$ trois points alignés d'une part, et $P\;,\ O\;,\ I$ trois points alignés d'autre part, dans le même ordre.

 

Calculons les rapports $\dfrac{PA}{PI'}\quad\text{et}\quad\dfrac{PO}{PI}$

 

On a :

 

$\dfrac{PA}{PI'}=\dfrac{3\sqrt{2}}{4\sqrt{2}}=\dfrac{3}{4}=0.75$

 

$\dfrac{PO}{PI}=\dfrac{4.5}{6}=0.75$

 

Ce qui montre que : $\dfrac{PA}{PI'}=\dfrac{PO}{PI}$

 

Par conséquent, la réciproque du théorème de Thalès permet de conclure que les droites $(OA)\ $ et $\ (II')$ sont parallèles.