Dénombrement et probabilité - 1er L
Classe:
Première
Analyse combinatoire - Probabilité
I Ensembles Finis
1.Définition
$\bullet\ $Un ensemble $E$ fini, est un ensemble dont on peut compter les éléments.
$\bullet\ $Le nombre d'élément de l'ensemble $E$ est appelé cardinal de $E$ on le bote $\text{Card}E.$
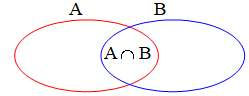
$\bullet\ $La réunion de deux ensembles $A$ et $B$ notée $A\cap B$ est l'ensemble des éléments qui sont dans $A$ ou bien dans $B$.
$\bullet\ $L'intersection de deux ensemble $A$ et $B$ notée $A \cup B$ est l'ensemble des éléments qui sont à la fois dans $A$ et dans $B$
Remarque:
$\bullet\ $Si $E$ est un ensemble vide alors $\text{Card}E=0.$
$\bullet\ $Dénombrer un ensemble fini $E$, c'est calculer son cardinal.
2. Propriété
a. Réunion d'ensembles finis:
Propriété 1 :
La réunion de deux ensembles fini disjoints $A$ et $B$ est un ensemble fini dont la cardinal $St$ égale à la somme des cardinaux.
Autrement dit: Si $A\cup B$ est un ensemble fini dont le cardinaux dit: Si $A\cup B=\Phi$, alors $\text{Card}A\cap B=\text{Card}A+\text{Card}B$
Propriété 2 :
Quels que soient les ensembles finis $A$ et $B$ :
$\text{Card}A\cap B=\text{Card}A+\text{Card}B-\text{Card}A\cup B$
Exercice d'application :
Dans une classe de $40$ élèves, chacun doit étudier au moins une langue ; vingt cinq étudient l'espagnole, trente étudient l'allemand.
Combien d'élèves font les deux langues
Solution :
Soit $A$ l'ensemble des élèves qui étudient l'espagnole et $B$ l'ensemble des élèves qui étudient l'allemand.
On a $\text{Card}A\cap B=\text{Card}A+\text{Card}B-\text{Card}A\cup B$
Donc $\text{Card}A\cup B=\text{Card}A+\text{Card}B-\text{Card}A\Cap B$
$=25+30-40=15$
Donc $15$ élèves font les deux langues.
b.Complémentaires
Soit $E$ un ensemble fini et $A$ un sous ensemble de $E$ L'ensemble $E/A$ est le complémentaire de $A$ dans $E.$
On le note $C_{E}A$ ou $\overline{A}$ alors $E=A\cap\overline{A}$ et $A\cup\overline{A}=\Phi$ et $\overline{A}$ donc $\text{Card}\overline{A}=\text{Card}E–\text{Card}A.$
c. Cardinal d'un produit cartésien.
Soit $A$ et $B$ des ensembles finis non vides, le produit cartésien $A\times B$ est l'ensemble des éléments $(x\;,\ y)$ tel que $x\in A$ et $y\in B.$
Propriété :
Le produit cartésien de deux ensembles finis $A$ et $B$ est fini et que :
$\text{Card}A\times B=(\text{Card}A)\times(\text{Card}B)$
II Dénombrement
1. $p-$listes d'un ensemble fini
a. Définition
Soit $E$ un ensemble fini non vide et $p$ un entier naturel non nul.
On appelle $p$-liste d'élément de $E$ tout élément de $E_{p}$
L'ordre des éléments est important, la répétition est possible..
Exemple
$(b\ ;\ a\ ;\ c\ ;\ c\ ;\ c\ ;\ a\ ;\ l\ ;\ a\ ;\ u\ ;\ r\ ;\ e\ ;\ a\ ;\ t)$ est un $12-liste$ d'élément de $E={a\ ;\ b\ ;\ c\ ;\ e\ ; 1\ ;\ r\ ;\ t\ ;\ u}$
Théorème
Le nombre de $p$-liste d'un ensemble fini à $n$ éléments est $n^{p}$
b. Exercices d'application
I. une urnes contient $5$ jetons numérotés de $1$ à $5$.
On effectue $4$ tirages successifs avec remise.
1. Donner un résultat possible.
2. Déterminer le nombre de résultats possibles.
II On jette trois fois de suite un pièce de monnaie en notant à chaque fois la partie située au dessus.
En utilisant un arbre déterminer le nombre de résultats possibles.
2. Arrangement
a. Définition
Soit $E$ un ensemble fini à $n$ éléments, un arrangement de $p$ éléments ou $p$ arrangement de $E$ est une $p$-liste formée d'élément deux à deux distincts $E(p\leq n)$
L'ordre des éléments est important et la répétition impossible..
Exemple :
soit $E=\left\lbrace a\ ;\ b\ ;\ c\ ;\ e\ ;\ l\ ;\ r\ ;\ t\ ;\ u\right\rbrace$
$(b\ ;\ a\ ;\ c)$ est arrangement de $3$ éléments de $E$
Théorème :
Soit $E$ un ensemble fini non vide de cardinal $n$ et $p$ un entier tel que $1\leq p\leq n.$
Le nombre d'arrangement d'ordre $p$ de $E$ est égal à :
$n\times(n-1)\times\ldots\times(n-p+1).$
Remarque :
Le nombre d'arrangement de $p$ éléments de $E$ est noté $A_{n}^{p}.$
Et $A_{n}^{p}=n\times(n-1)\times\ldots\times(n-p+1)=\dfrac{n !}{(n-p)!}$
Pour déterminer le nombre d'arrangements de $p$ éléments d'un ensemble $E$ à $n$ éléments, on peut utiliser un arbre de choix à $p$ niveaux :
Il y 'a $n$ choix possibles pour le premier élément ;
Il y 'a $(n-1)$ choix possibles pour le $2^{ème}$ élément ;
Il y 'a $(n-2)$ choix possibles pour le $3^{ème}$ élément ;
$\vdots$
$\vdots$
il y' a $n-(p-1)$ éléments possibles pour le $p^{ème}$ élément.
On en déduit que le nombre d'arrangements de $p$ éléments de $E$ est :
$n\times(n-1)\times\ldots\times(n-p+1).$
On rappelle que $n\ !\ =n(n-1)(n-2)\ldots 2\times 1$ $($se lit $n$ factorielle, ou factorielle $n)$ et que par convention $0\ !\ =1.$
b. Exercices d'application
I. Vingt chevaux participent à une course.
On appelle tiercé l'arrivée des trois premiers.
Déterminer le nombre de tiercé, en supposant qu'il n'y a pas d'ex æquo.
II. Déterminer le nombre de façon de placer $10$ personnes sur $15$ chaises sachant que $2$ personnes ne peuvent pas être sur la même chaise.
3. Permutation
Définition :
Soit $E$ un ensemble à $n$ éléments.
On appelle permutation de $E$ tout arrangement à $n$ éléments de $E.$
Propriété :
Le nombre de permutations d'un ensemble à $n$ éléments est $n$ !
Exemples :
1) Déterminer le nombre de façon de disposer cinq drapeaux de cinq pays différents.
2) On appelle anagramme d'un mot tout mot ayant un sens ou non formé avec les lettres qui le compose ; déterminer le nombre d'anagrammes des mots AFRIQUE ; ANAGRAMME.
4. Combinaison
Définition
Soit $E$ un ensemble à $n$ élément et $p$ un entier naturel tels que : $n\geq p.$
On appelle L'ordre des éléments n'est pas important.
Propriété
Le nombre de combinaisons de $p$ éléments d'un ensemble à $n$ éléments, noté $C_{n}^{p}$, est tel que :
$$C_{n}^{p}=\dfrac{A_{n}^{p}}{p!}=\dfrac{n!}{p!(n-p)!}$$
Remarque :
Soit $E$ un ensemble fini à $n$ éléments :
1. il y' a une seule partie à $0$ élément, c'est l'ensemble vide ; donc $C_{n}^{0}=1$
2. il y' a une seule partie à $n$ éléments, c'est l'ensemble $E$ lui-même ; donc $C_{n}^{n}=1.$
3. Il y' a n éléments dans $E$ donc $n$ singletons ; donc $C_{n}^{1}= n$
Exercices d'applications
1. un sac contient $15$ boules numérotée de $1$ à $15$, on tire simultanément $3$ boules dans le sac.
Déterminer le nombre de tirages possibles.
2. Dans une classe de $25$ élèves on choisit au hasard $5$ élèves pour représenter la classe à une réunion.
Déterminer le nombre de choix possibles.
Propriétés
Soit $n$ et $p$ deux entiers naturels tel que $n\geq p$
$\bullet\ C_{n}^{p}=C_{n}^{n-p}$ (évident par le calcul)
$\bullet\ $Si de plus $0<p<n$, alors on a : $C_{n-1}^{p-1}+C_{n-1}^{p}=C_{n}^{p}$
Principe multiplicatif
Si un ensemble fini $E$ peut se décomposer en un produit cartésien d'ensembles $E_{1}$, $E_{2}$, $\ldots$, $E_{p}$ alors on a $\text{Card}(E)=\text{Card}\left(E_{1}\right)\cdot\text{Card}\left(E_{2}\right)\ldots\text{Card}\left(E_{p}\right).$
Si pour réaliser une épreuve on utilise les mots « et » , « puis » on applique le principe multiplicatif.
Exemples :
1. Pour aller l'école Moussa doit porter un tenu comportant : un pantalon, une chemise, une paire de chaussures et un sac.
Il dispose de $5$ pantalons, $7$ chemises, $3$ paires de chaussures et $2$ sacs.
Déterminer le nombre de tenus possibles.
2. un sac contient $4$ jetons blancs et $3$ jetons noirs.
On tire successivement avec remise $5$ jetons dans le sac.
Déterminer le nombre de tirages contenant exactement :
$\bullet\ 4$jetons noirs.
$\bullet\ $Un seul jeton blanc en dernier position.
Principe additif :
Si $E_{1}$, $E_{2}$, $\ldots$, $E_{p}$ forment une partition de $E$ (ensemble fini).
Alors $\text{Card}(E)=\text{Card}\left(E_{1}\right)+\text{Card}\left(E_{2}\right)+\ldots+\text{Card}\left(E_{p}\right).$
Si pour réaliser une épreuve on peut utiliser le mot « ou » on applique le principe additif.
Exemple :
un sac contient $4$ jetons blancs et $3$ jetons noirs.
On tire successivement avec remise $5$ jetons dans le sac.
Déterminer :
$\bullet\ $le nombre de tirages unicolore.
$\bullet\ $Le nombre de tirage comportant au moins un jeton noir
$\bullet\ $Le nombre de tirage comportant au plus 2 jetons blancs
II. Probabilité
1. Vocabulaire et Définitions :
$\bullet\ $Définition 1 :
Une expérience aléatoire est une expérience dont on ne peut pas prévoir les résultats.
Dans une situation donnée, on effectue une expérience aléatoire.
On s'intéresse à l'ensemble $\Omega$ des résultats possibles :
$$\begin{array}{|l|l|} \hline \text{Langage ensembliste}&\text{Langage probabiliste}\\ \hline \bullet\text{ Ensemble des résultats possibles}&\bullet\text{ L'univers}\\ \hline \bullet\text{ Elément}&\bullet\text{ Eventualité}\\ \hline \bullet\text{ Sous-ensemble ou partie}&\bullet\text{ Evenementt}\\ \hline \bullet\text{ Ensemble vide}&\bullet\text{ Evénement impossible}\\ \hline \bullet\text{ Ensemble }\Omega&\bullet\text{ Evénement certain}\\ \hline \bullet\text{ Complémentaire d'un ensemble }A&\bullet\text{ Evénement contraire de }A\text{ noté }\overline{A}\\ \hline \bullet\text{ L'ensemble }A\cap B&\bullet\ A\cap B\text{ est l'événement }A\text{ et }B\\ \hline \bullet\text{ L'ensemble }A\cup B&\bullet\ A\cup B\text{ est l'événement }A\text{ ou }B\\ \hline \bullet\text{ Si }A\cap B=\Phi\text{ on dit que les deux}&\bullet\text{ Si }A\cap B=\Phi\text{ on dit que les deux}\\ \text{sous ensembles }A\text{ et }B\text{ sont disjoints}&\text{événements }A\text{ et }B\text{ sont incompatibles.}\\ \hline \end{array}$$
$\bullet\ $Définition 2 :
Une probabilité $p$ associe à chaque événement $A$ un nombre réel compris entre $0$ et $1$ noté $p(A)$, qui est la somme des probabilités des événements élémentaire de $A$ et qui vérifie les propriétés suivantes :
$\blacktriangleright\ P(\Omega)=1\;,\ p(\Phi)=0$, et pour tout $A\subset\Omega\;,\ p(\overline{A})=1-p(A).$
$\blacktriangleright\ $Lors que les événement $A$ et $B$ sont incompatibles : $p\left(A\cup B\right)=p(A)+p(B).$
$\blacktriangleright\ $Dans le cas général : $p\left(A\cup B\right)=p(A)+p(B)-p\left(A\cap B\right).$
2. Équiprobabilité :
Il y' a équiprobabilité si chaque événement élémentaire de l'univers $\Omega$ a la même probabilité d'être réalisé (dé parfait, pièce équilibré, boules indiscernables au toucher, tirage au hasard...).
Les situations d'équiprobabilité peuvent être modélisées par le tirage d'une boule parmi $n$ boules discernables dans une urne.
Soit $\Omega$ un univers sur lequel il y' a équiprobabilité, Pour tout événement $A$ :
$$P(A)=\dfrac{\text{card}A}{\text{card}\Omega}=\dfrac{\text{nombre de cas favorables}}{\text{nombre de cas possibles}}$$
En effet
Soit $n=\text{Card}\Omega$
Tout événement élémentaire a donc pour probabilité $\dfrac{1}{n}.$
L'événement $A$ est la réunion d'événements élémentaires disjoints, par exemple :
$A=\left\lbrace w_{1}\right\rbrace\cup\left\lbrace w_{2}\right\rbrace\cup\ldots\cup\left\lbrace w_{p}\right\rbrace\ ;\ p\leq n.$
$\begin{array}{lcl} \text{Donc }p(A)&=&p\left(w_{1}\right)+p\left(w_{2}\right)+\ldots+p\left(w_{p}\right)\\\\&=&\dfrac{1}{n}+\dfrac{1}{n}+\ldots+\dfrac{1}{n}\\\\&=&\dfrac{p}{n} \end{array}$
Remarque :
Tout problème portant sur l'équiprobabilité peut se ramener à un problème de dénombrement.
Exercices types corrigés
1. Une enquête est faite auprès des élèves d'un lycée.
Elle révèle que $30\%$ d'entre eux se sont absentés le mois précédent au moins $4$ fois.
D'après cette enquête, quelle est la probabilité pour qu'un lycéen, pris au hasard, se soit absenté au plus $3$ fois le mois précédent ?
Solution
Au plus une fois signifie :
$\bullet\ $Ne s'est jamais absenté, ou bien
$\bullet\ $S'est absenté une seule fois, ou bien
$\bullet\ $S'est absenté exactement deux fois, ou bien
$\bullet\ $S'est absenté exactement trois fois.
Ce qui nous incite à considérer l'événement contraire
Soit $A$ l'événement : « Le lycéen s'est absenté au plus $3$ fois le mois précédent. »
Alors $A$ est l'événement : « le lycéen s'est absenté au moins $4$ fois le mois précédent »
D'après l'énoncé $p(\overline{A})=\dfrac{30}{100}=0.3.$
Alors $p(A)=1-p(\overline{A})=1-0.3=0.7$
2. Un dé non truqué comporte six faces ainsi marquées : $1\ 1\ 1\ 2\ 2\ 4.$
On lance ce dé une fois.
On suppose que chaque face a la même probabilité de sortie.
Quelle est la probabilité d'obtenir une face marquée $1$ ou $2.$
Solution
La présence de la conjonction ou nous pousse à calculer $p\left(A\cup B\right)$
Soit $A$ l'événement $«$ la face sortie porte le numéro $1 »$ et $B$ l'événement : $«$ la face sortie porte le numéro $2 »$
On a $p\left(A\cup B\right)=p(A)+p(B)$ $\left(A\text{ et }B\text{ sont disjoints}\right)$
Or chaque probabilité a la même chance de sortie, donc :
$$P(A)=\dfrac{\text{nombre de cas favorable à}A}{\text{nombre de cas possibles}}$$
Comme il y' a trois faces portant le numéro $1$, $p(A)=\dfrac{3}{6}=\dfrac{1}{2}$
Il y' a aussi $2$ faces portant le numéro $2$ donc $p(B)=\dfrac{2}{6}=\dfrac{1}{3}$
Ainsi $p\left(A\cup B\right)=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}.$

Ajouter un commentaire