Devoir n° 15 - 2nd s

On donne $a=-0.0007\;,\ b=2\times 10^{2}$ et $c=6\times 10^{3}$

Écrire le nombre $A$ sous la forme $2^{n}3^{m}5^{p}7^{q}.$

$$A=\dfrac{(x^{2}y^{-2})^{-5}}{(z^{-2}y^{-3})^{-2}}$$

Les dénominateurs étant supposés non nuls, écrire plus simplement possible les nombres suivants :

$$A=\dfrac{1}{2a(2a-1)}+\dfrac{2a-1}{2a}-\dfrac{2a}{2a-1}\;,\quad B=\dfrac{3a^{2}+3ax}{a^{2}-x^{2}}+\dfrac{a^{2}-ax}{a^{2}-2ax+x^{2}}$$

$$C=\dfrac{b+c}{(a-b)(a-c)}+\dfrac{c+a}{(b-c)(b-a)}+\dfrac{a+b}{(c-a)(c-b)}$$

P1 (4 points)

 

On pose $A=\sqrt{46+6\sqrt{5}}$ et $B=\sqrt{46-6\sqrt{5}}$.

 

$X=A+B\;;\ Y=A-B$

 

1) Montrer que X et Y sont des réels positifs.

 

2) a) Calculer $A\times B\;;\ X^{2}$ et $Y^{2}.$

 

b) En déduire $X$ et $Y.$

 

3) a) Démontrer que $A=\dfrac{X+Y}{2}$ et en déduire $B$ en fonction de $X$ et $Y.$

 

b) Écrire $A$ et $B$ sous la forme $a+b\sqrt{c}$  avec $a\;,\ b\;,\ c$ trois nombres relatifs.

 

c) Calculer $\dfrac{1}{A}+\dfrac{1}{B}$ et $\dfrac{1}{A}-\dfrac{1}{B}$

 

P2 (1.5 points)

Les lettres désignant des réels choisis de façon que les expressions écrites aient un sens.

 

1) Démontrer l'identité $\sqrt{x+\sqrt{y}}=\sqrt{\dfrac{1}{2}(x+\sqrt{x^{2}-y})}+\sqrt{\dfrac{1}{2}(x-\sqrt{x^{2}-y})}$

 

2) En utilisant la question 1) montrer que : $\sqrt{3+\sqrt{5}}=\dfrac{\sqrt{10}+\sqrt{2}}{2}$

 

P3 (2 points) 

 

1) Soit $x$ et $y$ des réels strictement positifs .Prouver que $\sqrt{xy}\leq\dfrac{x+y}{2}$

 

2) En déduire les inégalités suivantes :

 

a) $8xyz\leq (x+y)(y+z)(z+x)$

 

b) $xyz(x+y+z)\leq x^{2}y^{2}+y^{2}z^{2}+z^{2}x^{2}\leq x^{4}+y^{4}+z^{4}$

$ABC$ un triangle.

 

On définit les points $E\;,\ F$ et $I$ tels que : $5\overrightarrow{EB}+2\overrightarrow{AE}=\vec{0}\;;\ 3\overrightarrow{BF}-2\overrightarrow{BC}=\vec{0}$ et $I$ milieu de $[EF].$

 

1) Construire les point $E\;,\ F$ et $I.$

 

2) Démontrer que les droites $(BI)$ et $(AC)$ sont parallèles.

 

3) Soit $K$ le point défini par $\overrightarrow{CK}=-\dfrac{1}{6}\overrightarrow{AC}$.

 

Démontrer que les points $E\;,\ F$ et $K$ sont alignés.

Soit $IJK$ un triangle. On note $A$ le symétrique de $K$ par rapport à $J\;;\ B$ le symétrique de $I$ par rapport

à $K$ et enfin $C$ le symétrique de $J$ par rapport à $I.$

 

1) a) Exprimer le vecteur $\overrightarrow{AK}$ en fonction des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AI}$ puis $\overrightarrow{AI}$ en fonction des vecteurs $\overrightarrow{AJ}$ et $\overrightarrow{AC}.$

 

b) Exprimer le vecteur $\overrightarrow{AJ}$ en fonction du vecteur $\overrightarrow{AK}$.

 

c) En déduire des résultats précédents que : $\overrightarrow{AK}=\dfrac{2}{7}(2\overrightarrow{AB}+\overrightarrow{AC})$.

 

2) Soit $P$ le point défini par : $\overrightarrow{BP}=\dfrac{1}{3}\overrightarrow{BC}$. 

 

Placer le point C et exprimer $\overrightarrow{AP}$ en fonction de $\overrightarrow{AB}$ et $\overrightarrow{AC}.$

 

3) Déduire des questions 1) et 2) que les points $A_;,\ K\;,\ J\;,\ P$ sont alignés.

 

4) Soit $Q$ le point défini $\overrightarrow{CQ}=\dfrac{1}{3}\overrightarrow{CA}$.

 

a) Exprimer le vecteur $\overrightarrow{BQ}$ en fonction des vecteurs $\overrightarrow{BA}$ et $\overrightarrow{BC}$ puis $\overrightarrow{BK}$ en fonction du vecteur $\overrightarrow{BI}.$

 

b) Exprimer le vecteur $\overrightarrow{BK}$ en fonction des vecteurs $\overrightarrow{BA}$ et $\overrightarrow{BC}.$

 

c) En déduire des résultats précédents que : $\overrightarrow{BK}=\dfrac{1}{7}(2\overrightarrow{BA}+2\overrightarrow{BC}$. 

 

En déduire de même que les points $B\;,\ K\;,\ I\;,\ Q$ sont alignés.

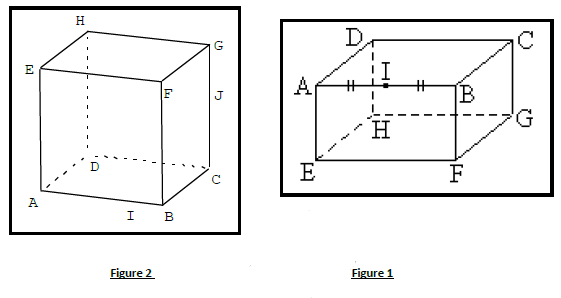
$ABCDEFGH$ est un cube. $M$ milieu de $[EF]\;,\ N$ milieu de $[HG]\;,\ L$ milieu de $[AB].\ (P)$ le plan $(CMN)$ (figure 1)

 

1) a) Montrer que les points $M\;,\ N\;,\ C\;,\ B$ sont coplanaires.

 

b) Montrer que les points $H\;,\ N\;,\ B\;,\ L$ sont coplanaires.

 

2) Montrer que la droite $(HL)$ et parallèle au plan $(P).$

 

3) Déterminer et construire les intersections de $(P)$ avec les faces du cube.

$ABCDEFGH$ est un prisme à base rectangulaire. Sur le segment $[BF]\;$, on construit les points $M$ et $N$ distincts de $B$ et $F$ et dans l'ordre $B\;,\ M\;,\ N\;,\ F.$ (figure 2)

 

1) a) Montre que $(AE)$ perce le plan $(NAG).$

 

b) Montrer $(GC)$ perce le plan $(MAD).$

 

2) Montrer que les plans $(NHG)$ et $(MAD)$ sont sécants suivant une droite $(\Delta)$ que l'on précisera.

 

3) Construire le point où $(\Delta)$ perce le plan $(ABF).$

 

N.B. Ceci était un sujet de composition pour plusieurs classes. La partie algèbre était commune à toutes ces classes. Pour la partie géométrie, on peut traiter au choix les deux exercices de géométrie plane ou les deux exercices de géométrie dans l'espace.

 

$$\text{Durée : 4 h}$$