Devoir n° 29 1e S

 

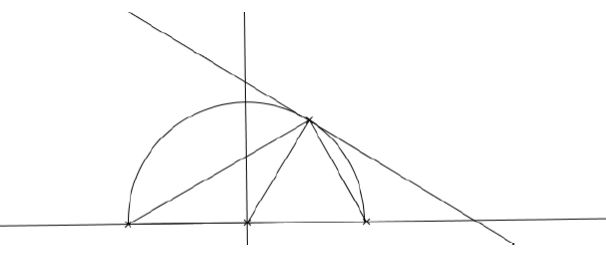
Soient un demi-cercle de centre $O$, de rayon $R$, de diamètre $[AB]\;,\ [OC]$ le rayon perpendiculaire à $(AB)\;,\ M$ un point du demi-cercle situé sur l'arc $BC$ , $D$ le point d'intersection de la droite $(AB)$ et de la tangente en $M$ au cercle.

 

On se propose de déterminer le point $M$ de façon que :

$$MA=m MD$$ ,

 

où $m$ est un paramètre réel strictement positif.

 

1) Soit $x$ une mesure en radians de l'angle orienté $\left(\overrightarrow{AB}\;,\ \overrightarrow{AM}\right).$

 

Justifier que : 

 

$\left(\overrightarrow{OB}\;,\ \overrightarrow{OM}\right)=2x[2\pi].$ 

 

Encadrer $x.$

 

2) Exprimer les distances $AM\text{ et }MD$ en fonction de $R\text{ et }x.$

 

En déduire que le point $M$ répond à la question si et seulement si $x$ vérifie les deux $u'\text{ et }u''$ conditions :

$$(I)\quad \left\lbrace\begin{array}{lcl} 2\cos x &=&m\tan x\\ 0<x &<&\dfrac{\pi}{4} \end{array}\right.$$

 

3) Exprimer $\tan 2x$ en fonction de $\sin x\text{ et }\cos x.$ 

 

En posant $u=\sin x$, démontrer que la résolution du système (I) se ramène à celle du système :

$$(II)\quad \left\lbrace\begin{array}{lcl} 2u^{2}+m\,u-1 &=&0\\ 0<u &<&\dfrac{\sqrt{2}}{2} \end{array}\right.$$  

 

4) On considère l'équation du second degré : 

 

$2 u^{2}+m\,u-1=0$

 

Montrer que cette équation admet deux racines $u'\text{ et }u''$ de signes contraires, puis classer $\dfrac{\sqrt{2}}{2}$ par rapport à $u'\text{ et }u''.$

 

5) Déduire de la question précédente que le système (II) admet, quel que soit $m\in\mathbb{R}^{+}$, une solution unique $u$ , dont on donnera l'expression en fonction de $m.$

 

6) Conclure quant au problème posé.

Soit $f$ la fonction définie par : 

 

$f(x)=\dfrac{\sqrt{1+x}+\sqrt{1-x}}{\sqrt{1+x}-\sqrt{1-x}}$

 

1) Déterminer l'ensemble de définition de $f.$

 

2) Démontrer que, pour tout $x$ élément de $D_{f}$ , on a :

 

$f(x)=\dfrac{1+\sqrt{1-x^{2}}}{x}$

 

3) Démontrer que la fonction $f$ est impaire.

 

4) Étudier $\lim_{x\rightarrow 1^{-}}\dfrac{f(x)-f(1)}{x-1}.$ 

 

Que peut-on en déduire ?

 

5) Sur quelle partie de $D_{f}$ la fonction $f$ est-elle dérivable ?

 

Déterminer sa fonction dérivée $f'.$

 

6) Dresser le tableau de variation de $f.$

Le plan est rapporté au repère orthonormé direct $(O\;,\ \vec{i}\;,\ \vec{j}).$ 

 

Soit $\mathcal{C}$ le cercle trigonométrique de centre $O\;,\text{ et }A_{0}\;,\ A_{1}\;,\ A_{2}\;,\ A_{3}\;,\ A_{4}$, les points de $\mathcal{C}$ tels que les angles

$(\vec{i}\;,\ \overrightarrow{OA_{k}})$ aient pour mesures respectives $\dfrac{2k\pi}{5}.$

 

1) Faire une figure. 

 

On constatera que les points $A_{0}\;,\ A_{1}\;,\ A_{2}\;,\ A_{3}\;,\ A_{4}$ sont les sommets consécutifs d'un pentagone régulier convexe.

 

2) Soit $\vec{S}$ le vecteur :

 

$\vec{S}=\overrightarrow{OA_{0}}+\overrightarrow{OA_{1}}+\overrightarrow{OA_{2}}+\overrightarrow{OA_{3}}+\overrightarrow{OA_{4}}.$

 

a) Démontrer que $\vec{S}$ est colinéaire à $\overrightarrow{OA_{0}}.$

 

b) Démontrer que $\vec{S}$ est aussi colinéaire à $\overrightarrow{OA_{1}}$

 

(Indication : $utiliser\ les\ coordonnées\ de\ points\ A_{0}\;,\ A_{1}\;,\ A_{2}\;,\ A_{3}\;,\ A_{4}\ dans\ le\ repère\ (O\;,\ \vec{i}\;,\ \vec{j})$

 

c) En déduire que $\vec{S}$ est le vecteur nul, puis les égalités :

 

$(1)\quad \sin\dfrac{2\pi}{5}+\sin\dfrac{4\pi}{5}+\sin\dfrac{6\pi}{5}+\sin\dfrac{8\pi}{5}=0$

 

$(2)\quad 1+\cos\dfrac{2\pi}{5}+\cos\dfrac{4\pi}{5}+\cos\dfrac{6\pi}{5}+\cos\dfrac{8\pi}{5}=0$

 

3) a) En utilisant l'égalité (2) précédente, démontrer que $\cos\dfrac{2\pi}{5}$ est une solution de l'équation : $4X^{2}+2X-1=0.$

 

b) Calculer : 

 

$\cos\dfrac{2\pi}{5}\;,\ \cos\dfrac{4\pi}{5}\;,\ \sin\dfrac{2\pi}{5}\;,\ \tan\dfrac{2\pi}{5}.$

 

4) Soit $\Omega$ le point de coordonnées $\left(-\dfrac{1}{2}\;;\ 0\right)$ et $J$ le point de coordonnées $(0\;,\ 1).$

 

a) Déterminer une équation du cercle $(\mathcal{C}$) de centre $\Omega$ et de rayon $\Omega\,J.$

 

b) Le point d'intersection du cercle $(\mathcal{C})$ et de l'axe des abscisses est positive est noté $K.$

 

Vérifier que l'abscisse de $K$ est $2\cos\dfrac{2\pi}{5}.$

 

c) Que représente la droite $(EB)$ pour le segment $[OK]$ ?

 

Déduire de ce qui précède une construction à la règle et au compas du pentagone régulier.

Dans cet exercice, on admettra le résultat suivant :

 

« Pour tout réel $a$ , il existe un unique réel $b$ tel $b^{3}=a$ ».

 

$b$ est appelé racine cubique de $a$ et noté $\sqrt[3]{a}.$

 

On considère deux réels $p\text{ et }q$ tels que :

 

$4p^{3}+27q^{2}>0$ et on note $f$ le polynôme défini pour $x$ réel par : 

 

$f(x)=x^{3}+px+q.$

 

1) Soit $u\text{ et }v$ deux réels solutions du système : 

$$(I)\quad\left\lbrace\begin{array}{lcl} u^{3}+v^{3}&=&-q\\ u\,v&=&-\dfrac{p}{3} \end{array}\right.$$  

 

Montrer que $f(u+v)=0.$

 

2) a) Résoudre le système : 

$$(II)\quad\left\lbrace\begin{array}{lcl} u^{3}+v^{3}&=&-q\\ u^{3}v^{3}&=&-\dfrac{p^{3}}{27} \end{array}\right.$$  

 

b) En déduire que le réel

 

$\alpha=\dfrac{1}{\sqrt[3]{2}}\left(\sqrt[3]{-q+\dfrac{1}{3}\sqrt{\dfrac{4p^{3}+27q^{2}}{3}}}+\sqrt[3]{-q-\dfrac{1}{3}\sqrt{\dfrac{4p^{3}+27q^{2}}{3}}}\right)$

 

est solution de l'équation $x^{3}+px+q=0.$ On admettra que c'est la seule.

 

3) On cherche à résoudre l'équation : 

 

$y^{3}+3y^{2}+\left(3-\sqrt[3]{2}\right)y+3=0\ (\ast).$

 

a) On effectue pour cela le changement de variable $y=x+h.$

 

Déterminer $h$ de façon que l'équation en $x$ obtenue à partir de $(\ast)$ soit de la forme $x^{3}+px+q=0.$

 

b) Calculer $p\text{ et }q$ et déterminer le signe de $4p^{3}+27\,q^{2}.$

 

c) Résoudre alors l'équation $(\ast).$   

                                                                                     Durée 4h