Devoir n°14 - 1e S1

$ABCDEF$ est un hexagone régulier inscrit dans le cercle trigonométrique. Donner la mesure principale, en radians, et une autre mesure en radians des angles orientés suivants :

 

 

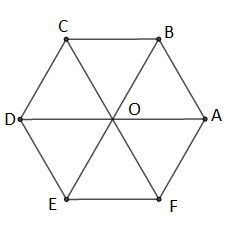
1) a) $(\overrightarrow{OA}\;,\ \overrightarrow{OF})\;;\quad$ b) $(\overrightarrow{OA}\;,\ \overrightarrow{FO})\;;\quad$ c) $(\overrightarrow{OC}\;,\ \overrightarrow{OA})\;;\quad$ d) $(\overrightarrow{AO}\;,\ \overrightarrow{CO})$ 

 

e) $(\overrightarrow{DF}\;,\ \overrightarrow{DC})\;;\quad$ f) $(\overrightarrow{EB}\;,\ \overrightarrow{EF})$

 

2) a) $(\overrightarrow{FC}\;,\ \overrightarrow{DE})\;;\quad$ b) $(\overrightarrow{FD}\;,\ \overrightarrow{FE})\;;\quad$ c) $(\overrightarrow{AB}\;,\ \overrightarrow{CD})$

$ABC$ est un triangle et $J$ un point du segment $[BC].$

 

Pour la suite, on utilisera le repère cartésien $(A\;,\ \overrightarrow{AB}\;,\ \overrightarrow{AC}).$

 

1) Quelles sont les coordonnées de $B$ et $C\;$ ?

 

2) $(Bu)\;,\ (Cv)\;,\ (AJ)$ sont des droites de coefficients respectifs $a\;,\ a'\;,\ \alpha.$

 

De plus, $(Bu)$ coupe $(AC)$ en $P\;;\ (Cv)$ coupe $(AB)$ en $Q\;$, les droites $(Bu)$ et $(Cv)$ se coupent sur la

droite $(AJ)$ au point $K$ distinct de $A.$

 

a) Déterminer les coordonnées des points $P\;,\ Q$ et $K$ en fonction de $a$ et $a'.$

 

b) Montrer que $a(1+a')=\alpha(1+a).$

 

3) a) Déterminer les coordonnées du point d'intersection $O$ (lorsqu'il existe) des droites $(BC)$ et $(PQ).$

 

b) Montrer que ces coordonnées sont indépendantes des réels $a$ et $a'.$

 

Que peut-on en déduire ?

 

4) Démontrer que $$\dfrac{\overline{CO}}{\overline{CJ}}=-\dfrac{\overline{BO}}{\overline{BJ}}$$

La droite $(AJ)$ est appelée la polaire du point $O$ par rapport aux droites $(AB)$ et $(AC).$

 

5) $\Delta$ et $\Delta'$ sont des droites sécantes en $A.\;\ O$ est un point qui n'appartient pas à $\Delta$ et $\Delta'.$

 

Construire la polaire du point $O$ par rapport aux droites $\Delta$ et $\Delta'.$

On considère les applications $f$ et $g$ ainsi définies : $$f(x)=\left\lbrace\begin{array}{rcl} 1-x&\text{si}&x<0 \\ x^{2}&\text{si}&x\geq 0\end{array}\right.\quad\text{et}\quad g(x)=\dfrac{1-x^{2}}{1+x^{2}}$$

1) Déterminer la fonction $f\circ g.$

 

2) L'application $f$ est-elle injective ? surjective ?

Soient $A\;,\ B\;,\ C$ et $M$ 4 points d'un axe $\Delta.$

 

Démontrer les égalités suivantes :

 

1) $\overline{MA}.\overline{BC}+\overline{MB}.\overline{CA}+\overline{MC}.\overline{AB}=0\quad$ (Euler).

 

2) $MA^{2}.\overline{BC}+MB^{2}.\overline{CA}+MC^{2}.\overline{AB}+\overline{BC}.\overline{CA}.\overline{AB}=0\quad$ (Stewart).

 

 

$$\text{Durée : 3 h}$$