EVALUATIONS STANDARISEES DU PREMIER SEMESTRE

Exercice 1

Soit $m$ un nombre  complexe différent de $1$

1.On considére dans l'ensemble $\mathbb{C}$,l'équation d'inconnue de z:

$(E):z^{2}-(1-i)(m+1)z-i(m^{2}+1)=0$

1-a)Vérifier que le discrimination de l'équation $(E)$ est $\Delta=[(1+i)(m-1)]^{2}$.

b)Résourdre dans $\mathbb{C}$ l'équation de$(E)$.

c)Déterminer sous forme algébrique les deux valeurs du complexe $m$ pour que le produit des deux solutions de l'équation de $(E)$ soit égal à $1$.

$$ \begin{array}{rcl}
I.1.a Δ &=& (1 − i)^{2}(m + 1)^{2} + 4i(m^{2} + 1) = −2i(m^{2} + 2m + 1) + 4im^{2} + 4i\\
              &=& 2im^{2} − 4im + 2i = 2i(m^{2} − 2m + 1) = (1 + i)^{2}(m − 1)^{2}\\
I.1.b z_{1} &=&\dfrac{(1−i)(m+1)−(1+i)(m−1)}{2}= 1 − im et \\
        z_{2} &=&\dfrac{(1−i)(m+1)+(1+i)(m−1)}{2}= m − i\\
I.1.c z_{1}z_{2} = 1&⟺&(1 − im)(m-i) = 1 \\
&⟺& m − z − m^{2}i − m = 1\\
                            &\Longleftrightarrow&{ m^{2}}=\dfrac{1+i}{i}= −1 + i
\end{array}$$
Posons $m = \alpha + i\beta$. On a alors :
$$\left\lbrace\begin{array}{rcl}
\alpha^{2} − \beta^{2} &= &−1\\
2\alpha\beta &=& 1, \text{système dont la résolution}\\
\alpha^{2}+ \beta^{2} &=& \sqrt{2}
\end{array}\right.$$
(élémentaire) conduit à : $m = −\sqrt{\dfrac{2-1}{2}}+ i\sqrt{\dfrac{2+1}{2}}$ ou $m = −\sqrt{\dfrac{2-1}{2}}− i\sqrt{\dfrac{2+1}{2}}$
 2.On pose $z_{1}=1-im$ et $z_{2}=m -i$.
Ecrrire $z_{1}$ et $z_{1}$ sous forme trigonometrique dans le cas ou $m=e^{i\theta}$ avec $\dfrac{\pi}{2}<\theta<\pi$.

Si$ m = e^{i\theta}$ , on a$$\begin{array}{rcl}
z_{1} = 1 − ie^{i\theta} &=& 1 − e^{i}(\dfrac{\pi}{2}+\theta)=e^{i}(\dfrac{\pi}{4}+\dfrac{\theta}{2})(e^{−i}(\dfrac{\pi}{4}+\dfrac{\theta}{2}) − e^{i}(\dfrac{\pi}{4}+\dfrac{\theta}{2}))\\
&=& −2i\sin(\dfrac{\pi}{4}+\dfrac{\theta}{2}) (\cos (\dfrac{\pi}{4}+\dfrac{\theta}{2}) + i\sin (\dfrac{\pi}{4}+\dfrac{\theta}{2}))\\
&=& 2 \sin (\dfrac{\pi}{4}+\dfrac{\theta}{2})(\sin (\dfrac{\pi}{4}+\dfrac{\theta}{2}) − i\cos (\dfrac{\pi}{4}+\dfrac{\theta}{2}))\\
&=& 2 \sin (\dfrac{\pi}{4}+\dfrac{\theta}{2})[\cos(\dfrac{\theta}{2}−\dfrac{\pi}{4}) + i \sin (\dfrac{\theta}{2}−\dfrac{\pi}{4}) ]
\end{array}$$
Les hypothèses faites sur $\theta$ entraînent que $\dfrac{\pi}{2}<\dfrac{\pi}{4}+\dfrac{\theta}{2}<\dfrac{3\pi}{4}$ et donc que : $\sin (\dfrac{\pi}{4}+\dfrac{\theta}{2}) > 0$. L’écriture précédente est bien la forme trigonométrique de $z_{1}$.

Et $$ \begin{array}{rcl}
z_{2} = e^{i\theta} − i &=& e^{i}(\dfrac{\pi}{4}+\dfrac{\theta}{2})(e^{i}(\dfrac{\pi}{4}-\dfrac{\theta}{2})−e^{i}(\dfrac{\pi}{4}-\dfrac{\theta}{2}))\\
&=& 2i \sin (\dfrac{\theta}{2}−\dfrac{\pi}{4}) (cos (\dfrac{\pi}{4}+\dfrac{\theta}{2}) +i\sin (\dfrac{\pi}{4}-\dfrac{\theta}{2}))\\
&=& 2\sin (\dfrac{\pi}{4}-\dfrac{\theta}{2}) (− \sin (\dfrac{\pi}{4}+\dfrac{\theta}{2}) + i \cos (\dfrac{\pi}{4}+\dfrac{\theta}{2}))\\
&=& 2 \sin (\dfrac{\pi}{4}+\dfrac{\theta}{2}) [\cos (\dfrac{3\pi}{4}+\dfrac{\theta}{2}) + i\sin (\dfrac{3\pi}{4}+\dfrac{\theta}{2})]
\end{array}$$
Ceci est la forme trigonométrique de $z_{2}$.

II.Le plan complexe $(P)$ est rapporté à un repére direct $\left(O.\vec{e_{1}}.\vec{e_{1}}\right)$.

On considére les points $M,M_{1}$ et $z_{2}$ d'affixes respectivement $m,z_{1}$ et $M_{2}$.

1.Determiner l'ensemble des points $M$ pour lesquels les points $M,M_{1}$ et $M_{2}$  sont alignés.                        
$M,M_{1}$ et $M_{2}$ sont alignés si et seulement si :
 $\dfrac{m−z_{1}}{m−z_{2}}\in\mathbb{R} \Longleftrightarrow \dfrac{m-1+im}{i}∈\mathbb{R}\Longleftrightarrow −im + i + m \in\mathbb{R}$.
Posons $m = x + iy$. La condition devient :
$(x + iy)(1 − i) + i \in\mathbb{R} \Longleftrightarrow {+ y + 1 = 0 }$: l’ensemble cherché est la droite d’équation $−x + y + 1 = 0$ privée du point $A (1,0)$.

2.Montrer que le nombre complexe $\dfrac{z_{2}−z_{1}}{z_{2}−m}$ est un imaginaire pur si et seulement si $Re(m)+Im(m)=1$.

$\dfrac{z_{2}−z_{1}}{z_{2}−m}=\dfrac{(m−i)−(1−im)}{(m−i)−m}$ est imaginaire pur si et seulement si : $(\dfrac{z_{2}−z_{1}}{z_{2}−m})= − (\dfrac{z_{2}−z_{1}}{z_{2}−m})\Longleftrightarrow \dfrac{\bar{m+i−1−im}}{i}=\dfrac{m−i−1+im}{i}$
Posons alors $m = x + iy$.

La condition précédente s’écrit $x − iy + i − 1 − i(x − y) = x + iy − i − 1 + i(x + iy)$

Soit : $2iy + 2ix − 2i = 0$ ou encore, en factorisant par $2i: x + y − 1 = 0$

Or $x = Re(m)$ et $y =Im(m)$, d’où le résultat.

Exercice 2:

Soit $f$la fonction définie sur $[1 ;\infty]$ par :$f(x)=\dfrac{1}{x}-ln\left(\dfrac{x+1}{x}\right)$.

En utilisant la fonction $f$,on se propose de déterminer la limite de la terme gégéral $S_{n}=\sum_{2n}^{k=n}\dfrac{1}{K}$

1.Soit $k$un entier nuturel non nul.Etablir les relations suivants:

a)$\dfrac{1}{k+1}\geq\int_{k}^{k+1}\dfrac{dx}{x}\geq\dfrac{1}{k}$

b)$\int_{k}^{k+1}\dfrac{dx}{x}=\dfrac{1}{k}=f(K)$

a) Soit $x \in [k; k+ 1]$. Alors on a $k ≤ x≤ k+1 ⟹\dfrac{1}{k+1}\geq\dfrac{1}{x}\geq\dfrac{1}{x}$

Par croissance de l’intégrale, on en déduit que :

$$\begin{array}{rcl}
&&\int_{k}^{k+1}\dfrac{dx}{k+1}\geq\int_{k}^{k+1}\dfrac{dx}{k+1}≤\int_{k}^{k+1}\\
&\Longleftrightarrow &\dfrac{1}{k+1}(k + 1 − k) ≤ \int_{k}^{k+1}\dfrac{dx}{k+1}≤\dfrac{1}{k}(k + 1 − k)\\
&⟺&\int_{k}^{k+1}\dfrac{dx}{x}≤\dfrac{1}{x}
\end{array}$$
b) $\int_{k+1}^{k}\dfrac{dx}{x}= [ln x]^{k+1}_{k} = ln (\dfrac{k+1}{k}) =\dfrac{1}{k}− f(k)$        

2.a)Déterminer deux réels $a$ et $b$ tels que $\dfrac{1}{x(x+1)}=\dfrac{a}{x}+\dfrac{1}{x+1}$.

b)Soit $U_{n}=\dfrac{1}{n(n+1)}+\dfrac{1}{(n+1)(n+2)}+.....+\dfrac{1}{2n(2n+1)}=\sum^{2n}_{k=n}\dfrac{1}{k(k+1)}$
    
Calculer $U_{n}$ en fonction de $n$ et déterminer $\lim\limits_{n\rightarrow +\infty}U_{n}$    

a)$a=1$ et $b=1$    (trivial)

b) D’après a), on a successivement :
$$\begin{array}{rcl}
\dfrac{1}{n(n+1)}=\dfrac{1}{n}-\dfrac{1}{n+1}\\
\dfrac{1}{(n+1)(n+2)}=    \dfrac{1}{n+1}-\dfrac{1}{n+2}\\
\dfrac{1}{(n+2)(n+3)}\dfrac{1}{n+2}-\dfrac{1}{n+3}\\
......................\
..............\\
\dfrac{1}{(2n-1)(2n)}=\dfrac{1}{2n-1}-\dfrac{1}{2n}\\
\dfrac{1}{2n(2n+1)}=\dfrac{1}{2n}-\dfrac{1}{2n+1}
\end{array}$$
Par addition membre à membre de ces $n + 1$ égalités, on obtient :    
$\sum^{k=2n}_{k=n}\dfrac{1}{k(k+1)}=\dfrac{1}{n}−\dfrac{1}{2n+1}=\dfrac{n+1}{n(2n+1)}$ et $\lim\limits_{n\rightarrow +\infty} \dfrac{n}{2n^{2}} = \lim\limits_{n\rightarrow +\infty} U_{n}\dfrac{1}{2n}= 0$    

c)Déduire des résultats de la qustion $(1)$    que $\sum^{2n}_{k=n}f(k)\geq U_{n}$.

d)Déterminer alors $\lim\limits_{n\rightarrow +\infty} \sum^{2n}_{k=n}f(k)$

e)Montrer 1.a$\dfrac{1}{k+1}\geq\sum^{2n}_{k=n}f(k)=S_{n}ln\left(\dfrac{2n+1}{n}\right)$.

En déduire $\lim\limits_{n\rightarrow +\infty}S_{n}\dfrac{1}{k + 1}≤\dfrac{1}{k}≤ −f(k) ≤\dfrac{1}{k}$ En soustrayant $\dfrac{1}{k}$    à chaque membre, il vient :
$\dfrac{1}{k + 1}−\dfrac{1}{k}≤ −f(k) ≤ 0$
d’où, en sommant membre à membre ces égalités de k allant de $n$ à $2n :
\sum^{k=2n}_{k=n} −\dfrac{1}{k(k+1)}\geq −f(k) ≤ 0$ puis en multipliant par −1 les trois membres :
$0 ≤ \sum^{k=2n}_{k=n}  −f(k)\geq \sum^{k=2n}_{k=n}−\dfrac{1}{k(k+1)}$
d) D’après le théorème des gendarmes, puisque $\lim\limits_{x\rightarrow +\infty}U_{n}=0$, il en résulte que
$\lim\limits_{x\rightarrow +\infty} \sum^{k=2n}_{k=n}  −f(k)= 0$
e) D’après 1.b,$ f(k) =\dfrac{1}{k}−\int^{k+1}_{k} \dfrac{dx}{x}$. D’où en sommant membre à membre de $k$
allant de $n$ à $2n$ et en utilisant la relation de CHASLES :
$\sum^{k=2n}_{k=n} f(k)= S_{n} − \int^{2n+1}_{n}\dfrac{dx}{x}$
On conclut en remarquant que : $\int^{2n+1}_{n}\dfrac{dx}{x}= ln \left(\dfrac{2n+1}{n}\right)$Puisque $\lim\limits_{n\rightarrow +\infty}\sum^{k=2n}_{k=n} f(k)=0$, on a $\lim\limits_{n\rightarrow +\infty}[S^{n} − ln \left(\dfrac{2n+1}{n}\right)] = 0$Or, $\lim\limits_{n\rightarrow\infty} ln\left(\dfrac{2n+1}{n}\right)= ln 2$ et par conséquent : $\lim\limits_{n\rightarrow +\infty} S_{n} = ln2$

Probleme

Le plan est muni d'un repére orthonormé $(O,\vec{i},\vec{j})$

Partie A:

On considére la fonction numérique $f$ définie sur l'intervalle $I=]-\dfrac{1}{2},\infty[$
$$\left\lbrace\begin{array}{rcl}
f(x)&=&\dfrac{ln(1+2x)}{x} si x\neq 0\\
f(0)&=&2
\end{array}\right.\text{et soit} (C_{f})\text{la courbe représentative de la fonction} f$$
1.Monttrer que la fonction $f$ est continue en $0$.
A.1 $\lim\limits_{x\rightarrow 0}\dfrac{ln(1+2x)}{x}= \lim\limits_{u\rightarrow 0}\dfrac{ln(1+u)}{\dfrac{1}{2}}u$(avec$u = 2x) = \lim\limits_{u\rightarrow 0} 2\dfrac{ln(1+u)}{u}= 2$ (d’après une limite usuelle)$ = f(0)$. $f$ est bien continue en $0$.

2.Pour tout réel non nul $a$ de l'intervalle $I$,on considére la fonction numérique $h_{a}$ définie sur $I$ par $h_{a}(x)=(ln(1+2a)-2a)x^{2}-(ln(1+2x)a^{2}$

a)Calculer $h_{a}(a)$ et $h_{a}(0)$,on déduire qu'il existe un réel $b$ compris entre $0$ et $a$ tel que:
$\dfrac{ln(1 + 2a) − 2a}{a^{2}}=\dfrac{-2}{1+2b}$

On a $h_{a}(a) = h_{a}(0) = 0. h_{a}$ est continue et dérivable sur $I$ comme somme et composée de fonctions dérivables sur $I$. En particulier elle l’est sur tout intervalle $l_{a}$ de bornes $0$ et $a$ et pour tout $x$ de $I$, on a :
$h_{a}′(x) = 2x[ln(1 + 2a) − 2a] − a^{2} \left(\dfrac{2}{1 + 2x}− 2\right)$
En appliquant le théorème des Accroissements Finis sur $l^{a}$, il existe $b \in l^{a}$ tel que :
$h_{a}(a) − h_{a}(0) = ah_{a}′(b)$
Soit :$ 2ab[ln(1 + 2a) − 2a] =\dfrac{−4a^{3}b}{1+2b}$. En simplifiant par $2ab$, on obtient :
$\dfrac{ln(1 + 2a) − 2a}{a^{2}}=\dfrac{−2}{1 + 2b}$
b)En déduire que $f$ est dérivable en $0$ et que $f'(0)=-2$.

$\lim\limits_{x\rightarrow 0}\dfrac{f(x)−f(0)}{x}= \lim\limits_{x\rightarrow 0}\dfrac{\dfrac{ln(1+2x)}{x}−2}{x}\lim\limits_{x\rightarrow 0}\dfrac{ln(1+2x)−2x}{x^{2}}{x\rightarrow 0}$

D’après ce qui précède, en remplaçant $x$ par $a , \lim\limits_{x\rightarrow 0}\dfrac{ln(1+2x)−2x}{x^{2}}= \lim\limits_{b\rightarrow 0}\dfrac{−2}{1+2b}$(où $b\in I{x}) = −2$.
$f$ est donc dérivable en $0$ et $f′(0) = −2$.

3.a)Montrer que la fonction $f$ est dérivable sur $I/{0}$  et que:
$\forall x \in {0};f'(x)=\dfrac{g(x)}{x^{2} (1+2x)}$ avec $g(x)=2x-(1+2x)ln(1+2x)$.

b)Montrer que $\forall x \in {0};g(x)<0$.

c)En déduire les variations de la fonction $f$ sur $I$
a)$f$ est dérivable sur chaque intervalle de $I \ {0}$ comme composée et quotient de fonctions dérivables sur cet intervalle.
Pour tout $x$ de $I \ {0}, f′(x) =\dfrac{2x−(2x+1) ln(2x+1)}{x²(2x+1)}$C.Q.F.D
b) Posons $u = 1 + 2x. g(x) = \delta(u) = −u ln u + (u − 1)$ avec $u > 0$ (on a posé $u = 2x + 1).\delta$ est dérivable sur
$]0; +∞[$ comme produit et somme de fonctions dérivables et $∀ u > 0, \delta′(u) = − ln u$ Le tableau de variation est :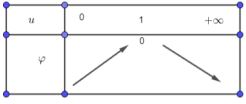

Il résulte de cette étude que $\delta$ est négative sur $]0; +\infty[$ et par suite que $g$ est négative sur $I \ {0}$. Or $f′$ a même signe que $g$ sur $I \ {0}$.$f$ est strictement décroissante sur $I$.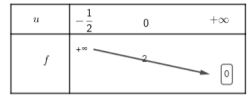

4.a)Calculer les deux limites $\lim\limits_{x\rightarrow (-\dfrac{1}{2})} 1 + 2x+0^{+}$ et $\lim\limits_{x\rightarrow+0^{+}} lnx=-\infty$
D'autre part  $\lim\limits_{x\rightarrow (-\dfrac{1}{2})^{0}}(x)=-\dfrac{1}{2} $.Par quotient et composée : $\lim\limits_{x\rightarrow \left(−\dfrac{1}{2}\right)} f(x) =+\infty$
Par ailleurs, $\lim\limits_{x\rightarrow+\infty} \dfrac{ln(1+2x)}{x}=\lim\limits_{x\rightarrow+\infty} \dfrac{ln(1+2x)}{1+2x}\times\dfrac{(1+2x)}{x}$Or,$\lim\limits_{x\rightarrow+\infty} \dfrac{ln(1+2x)}{1+2x}=\lim\limits_{v\rightarrow +\infty}\dfrac{ln v}{v}=0$ et$ \lim\limits_{x\rightarrow+\infty}\dfrac{1+2}{x}=2$(avec $v = 1 + 2x, v ⟶ +\infty$ quand $x ⟶ \infty )$.
Par produit, $ \lim\limits_{x\rightarrow+\infty}f(x) = 0$.

Interprétation géométrique : Les droites d’équations $x = −\dfrac{1}{2}$
et $y = 0$ sont asymptotes à la courbe $C_{f}$.
b) Au vu du tableau de variation précédent, $f$ est continue (elle est même
dérivable) sur $]−\dfrac{1}{2}; +\infty[$ et strictement décroissante sur $]−\dfrac{1}{2}; +\infty[$

réalise une bijection de $]−\dfrac{1}{2}; +\infty[$ vers son image par $f$ qui n’est autre que $]0; +\infty[$. Or, $1 \in ]0; +\infty[.$ Donc, $1$ a un unique antécédent par $f$. En d’autres termes, il existe un unique réel $\alpha ∈ ]−\dfrac{1}{2}; +\infty[$ tel que : $f(\alpha) = 1$.
$f(1) = ln 3 \cong 1$ et $f(2) =\dfrac{ln 5}{2}\cong 0.8$ donc $f(2) ≤ 1 ≤ f(1)$, soit :
$f(2) ≤ f(\alpha) ≤ f(1)$ et la stricte décroissance de $f$ sur $[1,2]$ entraîne que :$1 ≤ \alpha ≤ 2$

Partie B

1.On considère la fonction $\phi$ définie sur l'intervalle $I$ par:
$\phi(x)=ln(1+2x)$ et pose $J=[1;\alpha]$.

a)Montrer que la fonction $\phi$ est dérivable sur $I$ et que $\forall x\geq1;0<\phi'(x)\geq\dfrac{2}{3}$

b)Vérifier que $\phi(\alpha)=\alpha$ et que $\phi(J)$.

1°) a) $\phi$ est dérivable sur $]−\dfrac{1}{2}; +\infty[$ comme composée des fonctions dérivables $u: x \mapsto 1 + 2x$ (dérivable sur $\mathbb{R}$ comme fonction polynôme, donc en particulier sur $]−\dfrac{1}{2}; +\infty[ , \cup (]−\dfrac{1}{2}; +\infty[) \subset ]0; +\infty[)$ et $v:x↦ ln x$ est dérivable sur $]0; +\infty[$ donc a fortiori sur $u (]−\dfrac{1}{2}; +∞[)$.
Il en résulte que $\phi$ est dérivable sur $J = [1, \alpha]$.
$∀x \in I, \phi′(x) =\dfrac{2}{1+2x}$ et $x ≥ 1 ⟹ 1 + 2\geq 3⟹ \dfrac{1}{1+2x}≤\dfrac{1}{3}⟹\dfrac{2}{1+2x}≤\dfrac{2}{3}$ et sur $[1; +\infty[$, il est clair que $\dfrac{2}{1+2x}> 0$.
On a donc bien $0 < \phi′(x) ≤\dfrac{2}{3}$ sur $[1; +\infty[$.
b) L’égalité $f(\alpha) = 1$ (qui définit $\alpha$) s’écrit : $ln(1 + 2\alpha) = \alpha$, soit $\phi(\alpha) = \alpha$.
$ \phi′(x) > 0$ sur $[1; +\infty[$, donc $\phi$ est strictement croissante sur $[1; +\infty[$. Les inégalités $1 ≤ \alpha ≤ \alpha$ entraînent donc que : $\phi(1) ≤ \phi(x) ≤ \phi(\alpha) = \alpha$, soit $ln 3 ≤\phi(x) ≤ \phi(\alpha)$. Comme $ln 3 ≥ 1$, il en résulte que pour tout $x∈ J,$ on a $\phi(x) ∈ J$.
2.On considére la suite numérique $(U_{n})n\in\mathbb{N}$ définie par

$$\left\lbrace\begin{array}{rcl}
U_{0}&=&1\\
U_{n+1}&=&ln(1+U_{n}),\text{pour tout} n\in\mathbb{N}
\end{array}\right.$$

a)Montrer que:$\forall n\in\mathbb{N};U_{n}\in J$.

b))Montrer que:$\forall n\in\mathbb{N};|U_{n}-\alpha|\leq\left(\dfrac{2}{3}\right)^{n}$.

c)En déduire que $(U_{n})n\in\mathbb{N}$ est convergente et déterminer sa limite.

2°) a) Par récurrence sur $n$. La propriété est vraie pour $n = 0$ car $U_{0} = 1 ∈J$.
Supposons que $U_{n} ∈J$. Alors, d’après la question précédente, $U_{n+1}= \phi(U_{n}) ∈ J$.

b) La fonction $\phi$ est continue sur $J$ et dérivable sur $]1; \alpha[$. Pour tout $x$ de $J$, on a : $\phi
|phi′(x)| ≤\dfrac{2}{3}$d’après la question B.1.b.

Donc par application de l’Inégalité des Accroissements Finis à $\phi$ entre les éléments $U_{n+1}$ et $\alpha$ de $J (n ≥ 1)$, on a : $|\phi(U_{n−1}) − \phi(\alpha)| ≤\dfrac{2}{3}|U_{n−1} − \alpha|$, soit (puisque $\phi(U_{n−1}) = U_{n}$ et $\phi(\alpha) = \alpha) : |U_{n} − \alpha| ≤\dfrac{2}{3}|U_{n−1} − \alpha|$.

Si on écrit cette inégalité pour les entiers $k \in{1,2, … , n}$ et si on multiplie membre à membre ces $n$ inégalités, on obtient par « télescopage »
$|U_{n} − \alpha| ≤ \left(\dfrac{2}{3}\right)^{n}|U_{0} − \alpha|$

Et comme $|U_{0} − \alpha| ≤ 1$ (car $U_{0}$ et $\alpha$ sont tous deux dans $[1 ;2])$, on en déduit que l’on a bien : $|U_{n} − \alpha| ≤ \left(\dfrac{2}{3}\right)^{n}$.

c) Puisque $0 <\dfrac{2}{3}< 1$, une propriété des limites de suites géométriques entraîne que :$\lim\limits_{n\rightarrow+\infty}\left(\dfrac{2}{3}\right)^{n}=0$ et par suite $\lim\limits_{n\rightarrow+\infty}U_{n} = \alpha$.

La suite$ (U_{n})$ converge vers $\alpha$.

Partie C:

On considére la fonction $F$ définie sur l'intervalle $I$ par: $F(x)=\int^{x}_{O}f(t)dt$

1.a)Montrer que la fonction $F$ est dérivable $I$ puis  calculer $F'(x)$.

b)En déduire les variations de la fonction $F$ sur $I$.

1°) a) Rappelons que $f$ est continue sur $I$. Par définition de l’intégrale, $F$ est la primitive de $f$ sur$I$  qui s’annule en $0$, donc $F$ est dérivable sur $I$  et $\forall x∈ I, F′(x)x=f(x)$.

b) $f$ ne prenant que des valeurs positives sur $I, F$ est strictement croissante sur $I$.

2.a)Montrer que:$\forall x\geq 1 ;F(x)\geq \int^{x}_{1}\dfrac{ln(1+2t)}{1+2t}dt$

b)En déduire que :$\lim\limits_{x\rightarrow+\infty}F(x)=+\infty$.

2°) a) Soit $t \in [1, x]$. On a : $t ≤ 1 + 2t$ donc en passant aux inverses (ces nombres sont strictement positifs), on en déduit que : $\dfrac{1}{t}≥\dfrac{1}{1+2t}$(*). D’autre part, on $1 +2t ≥ t ≥ 1$, donc $ln(1 + 2t) ≥ 0$. Par multiplication des deux membres de l’inégalité (*) par $ln(1 + 2t)$, on obtient :$\forall t\in t[1, x] : \dfrac{ln(1+2t)}{t}≥\dfrac{ln(1+2t)}{1+2t}$

Il suffit alors d’intégrer les deux membres de $1$ à $x$ et d’utiliser la croissance de l’intégrale pour conclure.

2°) b) La fonction $g: t \mapsto\dfrac{ln(1+2t)}{1+2t}$ est de la forme $\dfrac{1}{2}$u′(t)u(t)$ avec $u(t) =ln(1 + 2t)$.

Elle a pour primitives les fonctions $G$ définies par $G(t)=\dfrac{1}{2}\dfrac{u^{2}(t)}{2}+ C (C \in\mathbb{R})$, soit $G(t) =ln^{2}\dfrac{(1 + 2t)}{4}+ C$
Il en résulte que : $\int^{x}_{1}\dfrac{ln(1+2t)}{1+2t}dt= [\dfrac{ln2(1+2t)}{4}]^{x}_{1}=\dfrac{ln2(1+2x)}{4}−\dfrac{ln 3}{4}$

Il est clair que cette expression tend vers $+\infty$ quand $x \mapsto +\infty$ (par produit et composée).

Et comme $F(x)$ est supérieure ou égale à cette expression, il résulte d’un théorème de comparaison des limites que :
$\lim\limits_{x\rightarrow+\infty}F(x)=+\infty$

On suppose que la fonction $F$ admet une limite dinie $I$ à droite en $-\dfrac{1}{2}$.

On considére la fonction $h$ définie sur l'intervalle $]-\dfrac{1}{2};+\infty[$ par:

$$\left\lbrace\begin{array}{rcl}
h(x)&=&F(x) si x\in I\\
h(-\dfrac{1}{2})&=&l
\end{array}\right.$$

a)En déduire le theoréme des acroissements finis,montrer que:
$\forall t∈ I,F(x)-1\geq f(x)\left(x+\dfrac{1}{2}\right)$.

nb)Etudier la dérivabilité de $h$à droite en $-\dfrac{1}{2}$.

3°) a) Soit $x ∈ I.$ Considérons la fonction $−h$ sur l’intervalle $[−\dfrac{1}{2}; x]$.
Cette fonction est continue sur $ [−x+\dfrac{1}{2}; x] $(car elle l’est sur $I$) et dérivable sur $ ]−\dfrac{1}{2}; x[$ et pour tout$t$de ce dernier intervalle, on a :

$f (−\dfrac{1}{2}) ≥ h′(t) =f(t) ≥ f(x)$ (ne pas oublier que $f$ est décroissante sur I) donc $−L ≤ −h′(t) ≤ −f(x)$.
Par application de l’Inégalité des Accroissements Finis à la fonction $(−h)$ sur $[−\dfrac{1}{2}; x]$, on obtient : $−L \left(x+\dfrac{1}{2}\right) ≤ −F(x) + L ≤ −f(x) \left(x+\dfrac{1}{2}\right)$
L’inégalité souhaitée s’obtient en multipliant l’inégalité $−F(x) + L ≤ −f(x) \left(x +\dfrac{1}{2}\right)$ par $(−1)$.

b) Or, $\lim\limits_{x\rightarrow\left(−\dfrac{1}{2}\right)^{+}}f(x)=+\infty$ (voir 4°) a de la partie A).

Comme $\dfrac{F(x)−L}{x+\dfrac{1}{2}}≥f(x)$ sur $I$, il en résulte par comparaison que
$\lim\limits_{x\rightarrow\left(−\dfrac{1}{2}\right)^{+}}\dfrac{h(x)−h\left(−\dfrac{1}{2}\right)}{x+\dfrac{1}{2}}=+\infty$.

$h$ n’est donc pas dérivable à droite en $−\dfrac{1}{2}$.