Exercices : Géométrie dans l'espace 5e
Classe:
Cinquième
Exercice 1
Représenter en perspective le parallélépipède et le cube sur une "feuille blanche".
Exercice 2
Représenter en perspective le prisme droit sur une "feuille blanche".
Exercice 3
1) Donner la définition d'un prime droit.
2) Un prime droit a six faces.
a) Combien de coté ont chacun de ses faces.
b) Quelle est la nature de ses bases.
Exercice 4
La figure ci-dessous représente le patron d'un prisme droit.
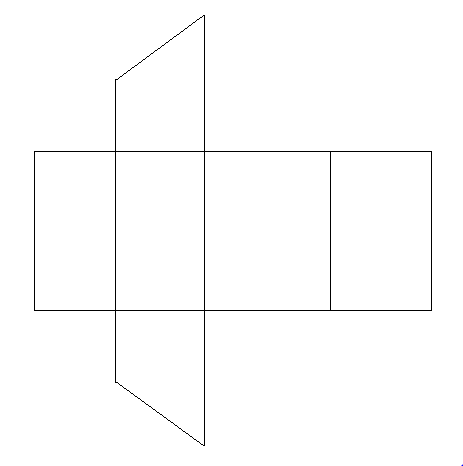
1) Reproduire cette figure ; puis coder les segments de même longueur, les faces latérales et les faces de la même base.
2) Quelle est la nature de sa base ?
3) Représenter ce prisme en perspective.
Exercice 5
Représenter le patron d'un prisme droit dont :
$-\ $ La hauteur mesure $6\;cm.$
$-\ $ Les bases sont des triangles isocèles dont les cotés ont pour longueurs $5\;cm\;;\ 5\;cm\ $ et $\ 4\;cm.$
Exercice 6
$ABCDEFGH$ est un prisme droit dont les bases $ABCD\ $ et $\ EFGH$, sont des trapèzes rectangles.
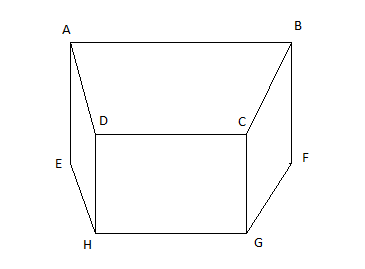
1) Nommer deux plans parallèles.
2) Nommer deux plans perpendiculaires.
3) Nommer deux plans sécants.
4) Nommer deux droites parallèles.
5) Nommer deux droites perpendiculaires
6) Nommer deux droites sécantes.
7) Nommer un plan et une droite parallèles.
8) Nommer un plan et une droite perpendiculaires.
9) Nommer un plan et une droite orthogonaux.
10) Nommer deux plans orthogonaux.
Exercice 7
1) Indique parmi les figures ci-dessous ceux qui représentent des prismes droits :
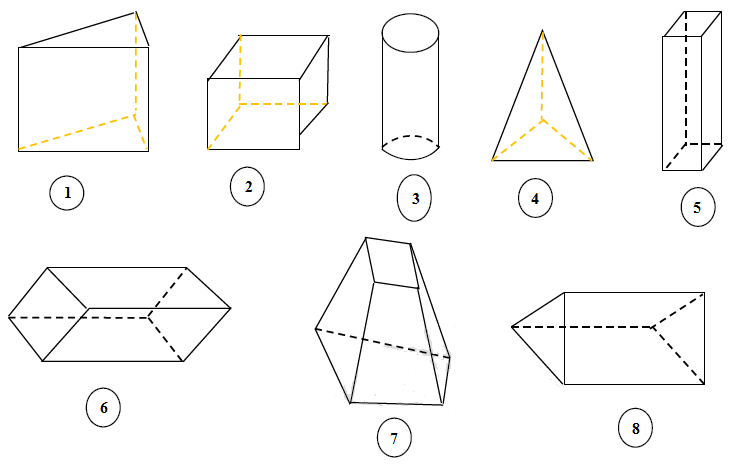
2) Deux de ces figures représentent des pavés droits. Lesquelles ?
Exercice 8
Recopie et complète les phrases ci-dessous en utilisant l'un des mots ou groupe de mots suivants : rectangles, carrés, bases, faces latérales, superposables. (Un mot ou groupe de mots peut être utilisé une ou plusieurs fois).
1) Dans un prisme droit, les $\ldots\ldots$ sont des rectangles. Les deux autres faces sont des polygones $\ldots\ldots$ appelées $\ldots\ldots$
2) Le parallélépipède rectangle est un prisme droit dont les $\ldots\ldots$ sont des $\ldots\ldots$ superposables.
3) Le cube est un prisme droit dont les $\ldots\ldots$ sont des $\ldots\ldots$ superposables.
Exercice 9
Parmi les figures ci-dessous, il y a deux patrons de prismes droits. Retrouve-les.
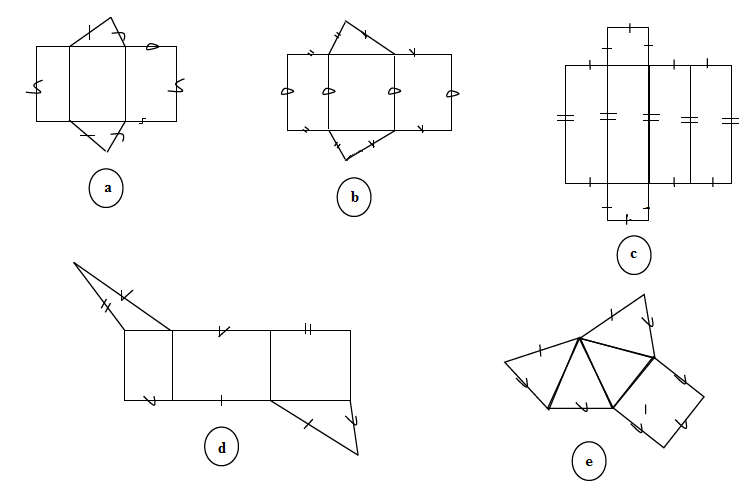
Exercice 10
La figure ci-dessous représente le patron d'un prisme droit dont une base est parallélogramme tel que $AB=4\;cm\;,\ BC=3\;cm\ $ et $\ PF=5\;cm$
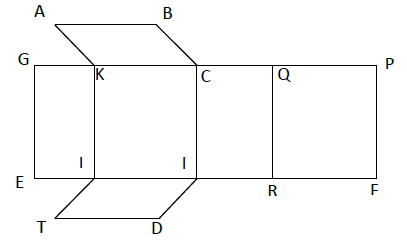
1) Reproduis cette figure, puis indique les côtés qui vont coïncider au collage.
2) Découpe la figure puis effectue le collage.
Exercice 11
Reproduis et complète chacune des figures ci-dessous de manière à obtenir des prismes droits :
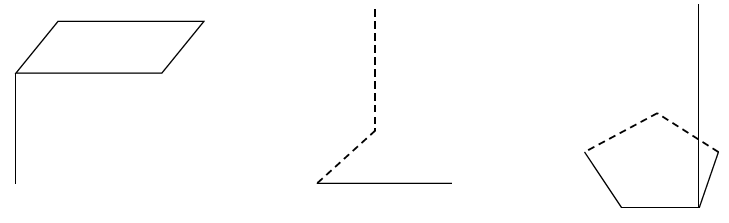
Exercice 12
La figure ci-dessous représente un prisme droit.
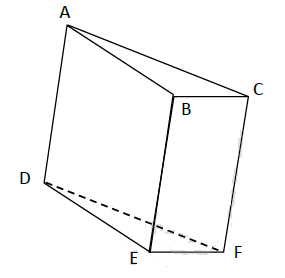
1) Cite dans cette figure :
$-\ $ Une droite perpendiculaire au plan $(EFD)$
$-\ $ Deux plans perpendiculaires
$-\ $ Deux plans parallèles
$-\ $ Deux droites parallèles
$-\ $ Deux droites perpendiculaires
$-\ $ Une droite parallèle au plan $(ABC)$
2) Soit $I$ le milieu du segment $[BC].$
Quelle est la position relative des droites $(DA)\ $ et $\ (AI)\ ?$
3) Les droites $(AD)\ $ et $\ (BC)$ sont-elles parallèles ? Sont-elles perpendiculaires ?
Exercice 13
La figure ci-dessous représente un prisme droit. (L'unité est le centimètre $(cm).$
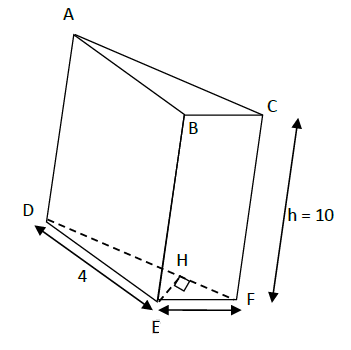
Sachant que $EH=2.4\ $ et $\ DF=6$
1) Calcule le volume de ce solide.
2) Calcule l'aire latérale de ce solide.
3) Détermine l'aire totale de ce solide.
Exercice 14
L'aire d'une base d'un prisme droit est égale à $15\;cm^{2}$ et sa hauteur $10\;cm.$
1) Calcule son volume.
2) Sachant que son aire totale est égale à $75\;cm^{2}$, calcule son aire latérale.
Exercice 15
Calcule l'aire latérale de chacun des prismes droits suivants :
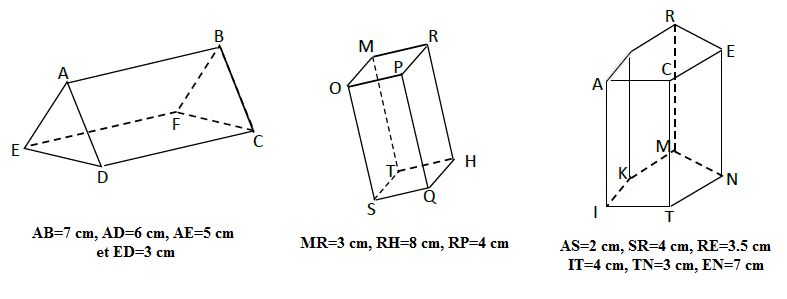
N.B : $OMRPSTHQ$ étant un parallélépipède rectangle.
Exercice 16
On a représenté ci-dessous un prisme droit dont une base est le trapèze isocèle $ABCD.$
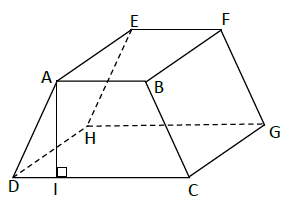
1) Cite :
$-\ $ Deux droites parallèles,
$-\ $ Deux droites perpendiculaires,
$-\ $ Deux droites qui ne sont ni parallèles, ni sécantes,
$-\ $ Deux plans perpendiculaires
$-\ $ Deux plans parallèles.
2) On donne : $DC=4\;cm\;,\ AE=3\;cm\;,\ AB=2.5\;cm\ $ et $\ AI=3\;cm.$
a) Calcule l'aire de la base $ABCD.$
b) Calcule l'aire latérale.
c) Calcule le volume de ce prisme.
Exercice 17
Soit le parallélépipède rectangle $ABCDEFGH$ ci-dessous
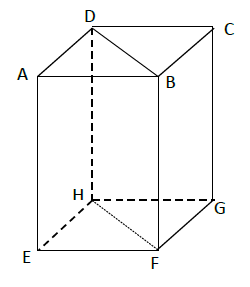
On donne $AB=6\;cm\;,\ BC=4\;cm\ $ et $\ CG=7\;cm.$
1) Calcule le volume de ce parallélépipède rectangle.
2) Soit le prisme droit déduit $ABDEFH.$
a) Représente ce prisme droit.
b) Représente le patron de ce prisme.
c) Calcule le volume de ce prisme.
Exercice 18
On donne un prisme droit $RECASONT$ de hauteur $10\;cm$, dont les bases, $SONT\ $ et $\ RECA$ sont des losanges de coté $5\;cm.$
Les diagonales $[SN]\ $ et $\ [OT]$ de la base $SONT$ mesurent respectivement $8\;cm\ $ et $\ 6\;cm.$
1) Représente ce prisme droit.
2) Dessine le patron de ce prisme.
3) Calcule son aire latérale.
4) Calcule son volume.
Exercice 19
Un container a la forme d'un parallélépipède rectangle d'aire de base $12\;m^{2}$ et de hauteur $2.5\;m$
On se propose d'y charger des cartons cubiques de coté $0.5\;m$
Combien de cartons peut-on y charger ?
Auteur:
Diny Faye & adem

Ajouter un commentaire