Fonction numérique : Limite et continuité - 1er L
Classe:
Première
I. Notion de limite
1. Activité :
Considérons la fonction $f$ définie sur $]1\;,\ +\infty[$ par :
$f\ :\ x\mapsto\;f(x)=\dfrac{3x-4}{x-1}$
$\blacktriangleright\ $Calculons ses valeurs $($arrondies à $10^{-5}$ prés par défaut$)$ lorsque la variable $x$ devienne de plus en plus grandes :
$$\begin{array}{|l|c|c|c|c|c|c|} \hline x&2&5&10&50&100&1000\\ \hline f(x)&2&2.75&2.88889&2.97959&2.98989&2.99989\\ \hline \end{array}$$
$\surd\ $On constate que lorsque les nombres $x$ deviennent de plus en plus grands, les nombres $f(x)$ s'approchent aussi près que voulu du nombre $3.$
On dira que la limite de $f$ en $\infty$ est égale à $3.$
$\surd\ $Calculons maintenant les valeurs de la fonction lorsque la variable $x$ s'approche de $\cancel \text{plus en plus de la valeur interdite 1.}$
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x&0.5&0.8&0.9&0.99&0.999&0.9999&\cancel 1&1.0001&1.001&1.01&1.1&1.2&1.5&2\\ \hline f(x)&5&8&13&103&1003&10003&&-9997&-997&-97&-7&-5&1&&2\\ \hline \end{array}$$
On constate, cette fois, que selon le côté dont on s'approche de la valeur interdite $1$ (droite ou gauche), les nombres $f(x)$ n'ont pas du temps le même comportement (puisque à droite les nombres $(f)$ deviennent de plus en plus proche de $+\infty$ tandis qu'à gauche ils deviennent de plus en plus proches de $-\infty.$
On dira que la fonction n'a pas de limite en $1.$
On pourra cependant nuancer en disant :
la limite de $f$ en $1$ à gauche est égale à $+\infty$
la limite de $f$ en $1$ à droite est égale à $\infty$
Évidemment, toutes ces considérations purement calculatoires, peuvent avoir un appui graphique :
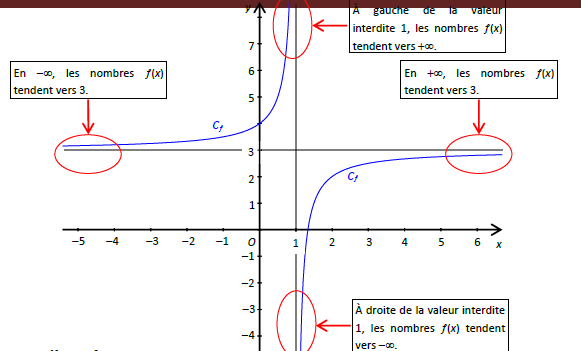
2. Limite d'une fonction en $+\infty$
Soit $f$ une fonction définie au moins sur un intervalle du type $[\alpha\;,\ +\infty.$
Lorsque $x$ prend des valeurs de plus en plus grandes :
$\blacktriangleright$ si les nombres $f(x)$ deviennent de plus en plus grands, on dit que $f$ a pour limite $+\infty$ en $+\infty$ et on note $\lim\limits_{x\rightarrow+\infty}.$
$\blacktriangleright$ si les nombres $f(x)$ deviennent de plus en plus grands en valeur absolue mais négatifs, on dit que $f$ a pour limite $-\infty$ en $+\infty$ et on note $\lim\limits_{x\rightarrow\;+\infty}f(x)=-\infty.$
$\blacktriangleright$ si les nombres $f(x)$ deviennent de plus en plus proches d'un réel $\ell$, on dit que $f$ a pour limite $\ell$ en $+\infty$ et on note $\lim\limits_{x\rightarrow +\infty}f(x)=\ell$

Ajouter un commentaire