La statistique descriptive - 1er S
Classe:
Première
L'origine du mot « statistique » remonte au latin classique status (état) qui, par une série d'évolutions successives, aboutit au français statistique, pour la première fois en $1771.$
La statistique trouve son application dans de nombreux domaines :
économie, biologie, commerce, et industrie, météorologie, physique, politique, sociologie...
Au collège l'enseignement de la statistique descriptive a pour objectif de familiariser les élèves à la synthèse d'informations sous forme numérique ou graphique.
Les documents étudiés prennent appui sur des situations de la vie quotidienne, sur des situations d'interdisciplinarité où on peut utiliser des donnés d'autres disciplines telles que la géographie, la démographie, histoire, biologie, physique,...
La synthèse d'informations sous forme numérique peut aboutir à des calculs de moyenne, de médiane, mode, pourcentage, fréquence, effectif, effectif cumulé croissant, effectif décroissant.
Ces calculs sont présents dans beaucoup de domaines autres que les mathématiques :
bulletin météo, indice de confiance des prévisions, sondages d'opinion, répartition des êtres vivants, vitesse moyenne, inaptitude dans la mesure, dispersion des mesures.
L'étude de la statistique nécessite la maitre la maitrise des ensembles des nombres tels que $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$, le repérage, la notion de droite dans un repère, la lecture de certaines représentations graphiques, de tableaux à deux lègues, de tableau à double entrée.
Série à un caractère
I. Définitions :
1) Population :
Une population est l'ensemble de référence sur lequel porte les observations, les prélèvements de données.
2) Unité statistique en individu :
Tout élément d'une population est appelé unité statistique ou individu
3) Effectif total :
L'effectif total est le nombre d'individus observés ou nombre d'individus de la population
4) Caractère :
On appelle caractère la propriété particulière d'un individu à laquelle on s'intéresse lors d'une observation, d'un prélèvement de données dans une population.
Un caractère peut être qualificatif ou bien quantitatif.
S'il est qualificatif, il peut être discret ou bien continue
a) Caractère qualificatif :
Lors d'une observation ne pouvant pas donner lieu à une mesure on dit que le caractère étudié est qualificatif
Exemple :
Lors d'une observation on peut s'intéresser à la « nationalité » de chaque individu ; le caractère « nationalité » ne se prête pas à une mesure ; on dit que c'est un caractère qualificatif.
b) caractère quantitatif :
Un caractère est quantitatif lorsqu'il est mesurable (on peut exprimer son intensité par un nombre)
$-\ \ $ Caractère quantitatif discret : Un caractère quantitatif est dit discret lorsqu'il prend des valeurs isolées peu nombreuses
$-\ \ $ Caractère quantitatif continu : Un caractère quantitatif est dit continu lorsqu'il peut prendre toute valeur d'un intervalle donné non vide de $\mathbb{R}$
Remarque :
$-\ \ $ On considère comme caractère continu un caractère discret dont le nombre de valeurs est grand ;
On regroupe ces valeurs dans des intervalles ou classes de la forme $\left[C_{i}\;,\ C_{i+1}\right[$ ; quand le nombre de valeurs d'un caractère est trop élevé, étudier séparément ces valeurs mène à des calculs longs fastidieux et sans intérêt ; on recueille de meilleurs informations en les regroupant dans les classes choisies de telle sorte à ne pas perdre les informations essentielles sur les individus observés.
$-\ \ $ La définition d'une population doit être univoque, non ambivalente, claire et ne doit souffrir d'aucune ambigüité.
C'est cela qui conditionne la fiabilité des résultats recueillis auprès de cette population.
5) Modalité :
$-\ \ $ Pour caractère quantitatif : une modalité est rubrique possible de ce caractère
Exemple :
Si on étudie, dans une population, le caractère « situation matrimoniale », les modalités de ce caractère sont :
marié, célibataire, veuf, divorce.
$-\ \ $ Pour un caractère quantitatif : les modalités sont les différentes valeurs d'enfants et on a obtenu les résultats suivants :
$$0-0-1-1-2-0-3-1-2-2$$
$-\ \ $ La population est l'ensemble des $10$ familles
$-\ \ $ chaque famille constitue un individu de cette famille
$-\ \ $ le caractère étudie est le caractère « nombre d'enfants »
$-\ \ $ ce caractère quantitatif discret peut prendre chacune des valeurs :
$$0\;,\ 1\;,\ 2\text{ et }3$$
Remarque :
Dans une population, un individu est associé à une seule modalité du caractère étudié.
Les modalités doivent permettre d'avoir une partition de la population $\Omega$ en des parties non vides, disjointes, de réunion $\Omega.$
6) Effectif $n_{i}$ :
L'effectif d'une modalité $n_{i}$ est le nombre $n_{i}$ de fois que cette modalité est observée.
Dans l'exemple précédent la valeur $n_{i}=0$ du caractère, est observée $3$ fois ; son effectif est alors $n_{i}=3$
7) Fréquence $f_{i}$ :
la fréquence $f_{i}$ d'une modalité $m_{i}$ est le quotidien $f_{i}=\dfrac{n_{i}}{n}$ où $n_{i}$ est l'effectif de cette modalité et $n$ l'effectif total
Remarque :
Il arrive qu'on ait besoin du nombre d'individus présentant au plus ou moins la valeur $x_{i}$ ou la fréquence $f_{i}$ d'un caractère quantitatif, on dit dans ce cas qu'on cumule de façon décroissante les effectifs ou les fréquences
$-\ \ $ Effectif cumulé croissant d'une valeur $x_{i}$ : c'est le nombre d'individu présentant une valeur du caractère inférieur ou égale à $x_{i}$ (ou une valeur au plus égale à $x_{i})$
Exemple :
Dans l'exemple précédent le nombre de familles qui ont au plus $2$ enfants est : $3+3+2+1=9$
On dit que la valeur $x_{3}=2$ du caractère à pour effectif cumulé décroissant $9$
8) Série statistique simple ou un caractère :
L'ensemble des couples $\left(x_{i}\;,\ n_{i}\right)$ ou l'ensemble des couples $\left(x_{i}\;,\ f_{i}\right)$, est appelé série statistique à un caractère
9) Présentation en tableau :
a) Caractère qualificatif :
$$\begin{array}{|c|c|c|c|c|} \hline \text{Modalités }m_{i}&m_{1}&m_{2}&\ldots&m_{3}\\ \hline \text{Effectifs }n_{i}&n_{1}&n_{2}&\ldots&n_{3}\\ \hline \text{Fréquences }f_{i}&f_{1}&f_{2}&\ldots&f_{3}\\ \hline \end{array}$$
b) caractère quantitatif discret :
$$\begin{array}{|c|c|c|c|c|} \hline \text{Valeur }x_{i}\text{ du}&x_{1}&x_{2}&\ldots&x_{k}\\ \text{caractère}& & & &\\ \hline \text{Effectifs }n_{i}&n_{1}&n_{2}&\ldots&n_{k}\\ \hline \text{Fréquences }f_{i}&f_{1}&f_{2}&\ldots&f_{k}\\ \hline \end{array}$$
On peut ajouter dans ce tableau : les effectifs cumulés et les fréquences cumulées
c) caractère quantitatif continu :
$$\begin{array}{|c|c|c|c|c|} \hline \text{Classes }C_{i}&\left[a_{1}\;,\ a_{2}\right[&\left[a_{2}\;,\ a_{3}\right[&\ldots&\left[a_{k}\;,\ a_{k}\right[\\ \hline \text{Centres }x_{i}\text{ des}&x_{1}&x_{2}&\ldots&x_{k}\\ \text{classes}& & & &\\ \hline \text{Effectifs }n_{i}&n_{1}&n_{2}&\ldots&n_{k}\\ \hline \text{Fréquences }f_{i}&f_{1}&f_{2}&\ldots&f_{k}\\ \hline \end{array}$$
On peut ajouter dans ce tableau les effectifs cumulés et les fréquences cumulées.
Remarque :
Le centre de la classe $\left[a_{i}\;,\ a_{i+1}\right[$ est $x_{1}=\dfrac{a_{1}+a_{i+1}}{2}$
L'amplitude de la classe $\left[a_{i}\;,\ a_{i+1}\right[$ est $a_{i+1}-a_{i}$
La densité de la classe $\left[a_{i}\;,\ a_{i+1}\right[$ est $d_{i}=\dfrac{n_{i}}{a_{i+1}-a_{i}}$
Lorsque les classes n'ont pas la même amplitude
II. Caractéristiques ou paramètres de position d'une série statistique simple ensemble des couples $\left(x_{i}\;,\ n_{i}\right)$ ou $\left(x_{i}\;,\ f_{i}\right)$, $i$ variant de $1$ à $k$ ; $f_{i}=\dfrac{n_{i}}{n}$ :
1) la moyenne $\bar{x}$ :
$$\overline{x}=\dfrac{1}{n}\sum_{i=1}^{k}x_{i}=\dfrac{x_{1}+x_{2}+\ldots+x_{k}}{n_{1}+n_{2}+\ldots+n_{k}}$$
$$\overline{x}=\sum_{i=1}^{k}f_{i}=\dfrac{f_{1}+f_{2}+\ldots+f_{k}}{n_{1}+n_{2}+\ldots+n_{k}}$$
2) les quantiles :
Définition :
On appelle quantile d'ordre $a\%$, noté $\mathcal{Q}_{a}$ la valeur $x_{i}$ du caractère telle que $a\%$ des valeurs observées soient inférieur ou égales à $x_{i}$
$-\ \ $ La médiane $M_{e}$ est le quantile d'ordre $50\%.$
Elle partage les valeurs de la série rangées dans l'ordre croissant, en deux sous-séries de même effectifs.
Il y a $50\%$ des valeurs inférieurs ou égales a $M_{e}$
$-\ \ $ Les quantiles $\mathcal{Q}_{1}$, $\mathcal{Q}_{2}$ et $\mathcal{Q}_{3}$ partagent la série en $4$ séries de même taille, lorsque les valeurs $x_{i}$ sont rangées dans l'ordre croissant : pour le premier quantile $\mathcal{Q}_{1}$ ou $\mathcal{Q}_{25}$, $25\%$ des valeurs sont inférieures ou égales à $\mathcal{Q}_{1}$ $50\%$ des observations sont inférieures ou égales à $\mathcal{Q}_{1}=\mathcal{Q}_{50}=M_{e}75\%$ des valeurs sont inférieures ou égales à $\mathcal{Q}_{3}=\mathcal{Q}_{75}$
$-\ \ $ Les $9$ déciles $\mathcal{Q}_{10}$, $\mathcal{Q}_{20}$, $\mathcal{Q}_{30}$, $\mathcal{Q}_{40}$, $\mathcal{Q}_{50}$, $\mathcal{Q}_{60}$, $\mathcal{Q}_{70}$, $\mathcal{Q}_{80}$ et $\mathcal{Q}_{90}$ partagent la série en $10$ séries de même effectif
3) le mode :
$-\ \ $ Pour une série correspondant à un caractère quantitatif discret, on appelle mode une valeur du caractère d'effectif maximum
Une série qui a plusieurs modes est dite plurimodale
Une série qui a un seul mode, noté $M_{0}$, est dite unimodale.
$-\ \ $ Pour un caractère quantitatif continu, dont les valeurs sont groupées en classes d'égales amplitudes, on appelle classe modale, la classe qui a le plus grand effectif.
Remarque :
Si les classes sont d'amplitudes inégales, une classe qui a le plus grand effectif, n'est pas forcément classe modale
III. Caractéristiques ou paramètres de dispersion d'une série ensemble des couples $\left(x_{i}\;,\ n_{i}\right)$ ou $\left(x_{i}\;,\ f_{i}\right)$, $i$ allant de $1$ à $k$ :
1) variance :
La variance est $$V(x)=\dfrac{\sum_{i=1}^{k}n_{i}\left(x_{i}-\overline{x}\right)^{2}}{\sum_{i=1}^{k}n_{i}}=\dfrac{n_{1}\left(x_{i}-\overline{x}\right)^{2}+n_{2}\left(x_{2}-\overline{x}\right)^{2}+\ldots+n_{k}\left(x_{2}-\overline{x}\right)^{2}}{n_{1}+n_{2}+\ldots+n_{k}}$$
On a aussi
$$V(x)=\sum_{i=1}^{k}f_{i}\left(x_{i}-\overline{x}\right)^{2}=f_{1}\left(x_{1}-\overline{x}\right)^{2}+f_{2}\left(x_{2} -\overline{x}\right)^{2}+\ldots+f_{k}\left(x_{k}-\overline{x}\right)^{2}$$.
Remarque :
On a aussi $V(x)=\dfrac{n_{1}x_{1}^{2}+n_{2}x_{2}^{2}+\ldots+n_{k}x_{k}^{2}}{n_{1}+n_{2}+\ldots+n_{k}}-\overline{x}^{2}$
Cette dernière formule est appelé théorème de Koenig.
2) Écart-type : $\sigma(x)=\sqrt{V(x)}$
L'écart-type d'une série statique est la racine carrée de sa variance
Remarque :
L'écart-type s'exprime dans la même unité que les valeurs $x_{i}$ du caractère et permet de mesurer la dispersion de ces valeurs autour de la moyenne $\overline{x}$ ; plus $\sigma(x)$ est grand plus cette dispersion est importante ; plus $\sigma(x)$ est petit plus les $x_{i}$ se resserrent autour de $\overline{x}.$
3) Coefficient de variation $CV=\dfrac{\sigma}{x}$ :
Le coefficient de variation $CV$ est le quotient de l'écart-type $\sigma(x)$ à la moyenne $\overline{x}.$
Il permet de comparer des séries dont les caractères de même nature mesurés avec des unités différentes, quant à la dispersion des valeurs autour de la moyenne $x.$
4) Écart absolu moyen par rapport à la moyenne :
$e_{\overline{x}}=\dfrac{n_{1}|x_{1}-\overline{x}|+n_{2}|x_{2}-\overline{x}|+\ldots n_{1}+n_{k}|x_{k}-\overline{x}|}{n_{1}+n_{2}+\ldots+n_{k}}=f_{1}\left(x_{1}-\overline{x}\right)+f_{2}\left(x_{2}-\overline{x}\right)+\ldots+f_{k}\left(x_{k}-\overline{x}\right)$
5) Écart absolu moyen par rapport à la médiane :
$e_{M_{e}}=\dfrac{n_{1}|x_{1}-M_{e}|+n_{2}|x_{2}-M_{e}|+\ldots+n_{k}|x_{k}-M_{e}|}{n_{1}+n_{2}+\ldots+n_{k}}$
$e_{M_{e}}=f_{1}\left|x_{1}-M_{e}\right|+f_{2}\left|x_{2}-M_{e}\right|+\ldots+f_{k}\left|x_{k}-M_{e}\right|$
On a :
$e_{M_{e}}\leq e_{\overline{x}}\leq\sigma(x)$
6) Écart-interquartile :
On appelle intervalle interquartile, l'intervalle $\left[\mathcal{Q}_{1}\;,\ \mathcal{Q}_{3}\right]$ contenant $50\%$ des observations centrales, formé du premier et du dernier quartile.
Son amplitude $\mathcal{Q}_{3}-\mathcal{Q}_{1}$ est appelée écart-interquartile.
Cet écart permet de mesurer la dispersion des valeurs de la série autour de la médiane.
7) Étendue :
L'étendue d'une série est égale à la différence entre la plus grande valeur et la plus petite valeur observées.
Remarque :
La boite à moustaches ou diagramme à boite :
Elle permet de faire apparaitre dans un diagramme les valeurs minimales, le premier quartile, la médiane, le troisième quartile et la plus grande valeur observée.
Elle permet de comparer des séries selon les ces $5$ paramètres et l'intervalle interquartile et l'étendue de chaque série
Exemple :
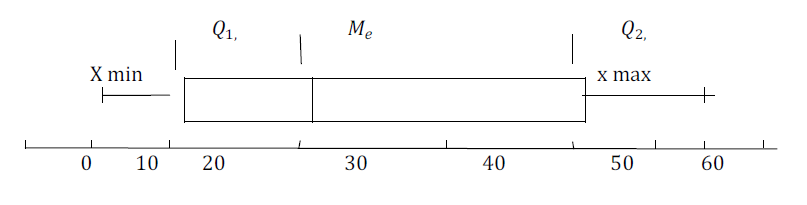
Cette boite à moustache permet d'avoir :
$\bullet$ $X_{min}=10$, la plus petite valeur du caractère
$\bullet$ $X_{max}=65$, la plus grande valeur du caractère
$\bullet$ les quartiles $\mathcal{Q}=20$, $M_{e}=30$ et $\mathcal{Q}_{3}=50$
IV. Représentations graphiques :
1) pour un caractère quantitatif :
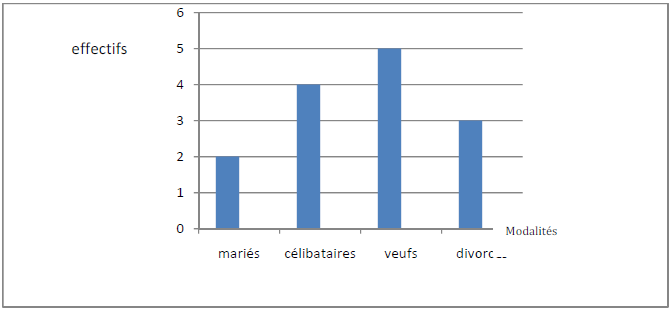
a) Diagramme à bandes :
On place sur une droite horizontale les modalités du caractère et on porte sur un axe vertical les effectifs $n_{1}$ ou les fréquences $f_{i}.$
Chaque modalité est représentée par une bande verticale dont la hauteur est proportionnelle à l'effectif de cette modalité
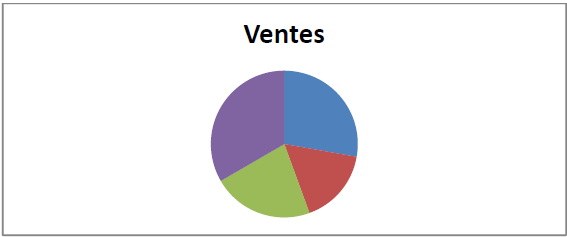
b) Diagramme circulaire ou diagramme à secteurs :
Un disque représente l'effectif total et chaque modalité est représentée par un secteur angulaire dont le sommet est le centre du disque et dont l'aire est proportionnelle à l'effectif $n_{i}$ de cette modalité.
La valeur $\alpha_{i}$ de l'angle au centre de ce secteur est calculée :
$\alpha_{i}=\dfrac{360\times n_{i}}{n}$ où $n$ est l'effectif total
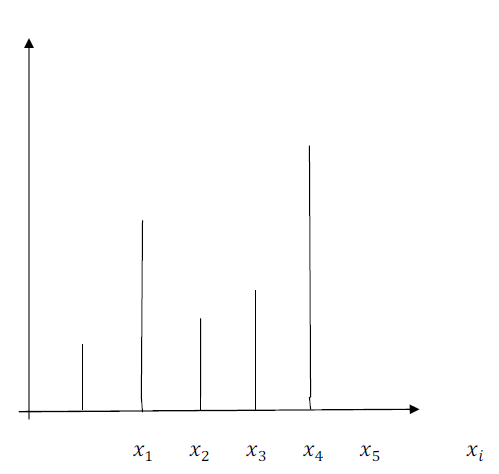
2) caractère quantitatif discret :
Diagramme en bâtons :
On met en abscisse les valeurs $x_{1}$, $x_{2}$, $\ldots$, $x_{k}$ du caractère, rangées dans l'ordre croissant et en ordonnée les effectifs respectifs $n_{1}+n_{2}+\ldots+n_{k}$ de ces valeurs.
On trace en $x_{1}$, $x_{2}$, $\ldots$, $x_{k}$ des bâtons de hauteurs $n_{1}+n_{2}+\ldots+n_{k}$ (on peut mettre en ordonnée les fréquences $f_{1}$, $f_{2}$, $\ldots$, $f_{k}$
3) Caractère quantitatif continu :
a) histogramme :
Un histogramme est un ensemble de rectangles contigus, chaque rectangle représentant une classe et ayant une aire proportionnelle à l'effectif de cette classe.
$\bullet$ Dans le cas où les classes ont la même amplitude, chaque rectangle à pour base la classe correspondante et pour hauteur l'effectif de cette classe
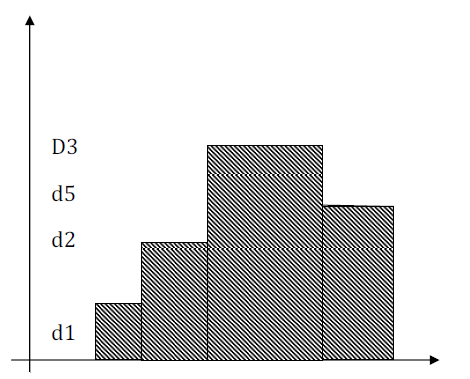
$\bullet$ Dans le cas où les classes n'ont pas la même amplitude, les bases des rectangles sont les classes et les hauteurs les densités $d_{i}$ des classes
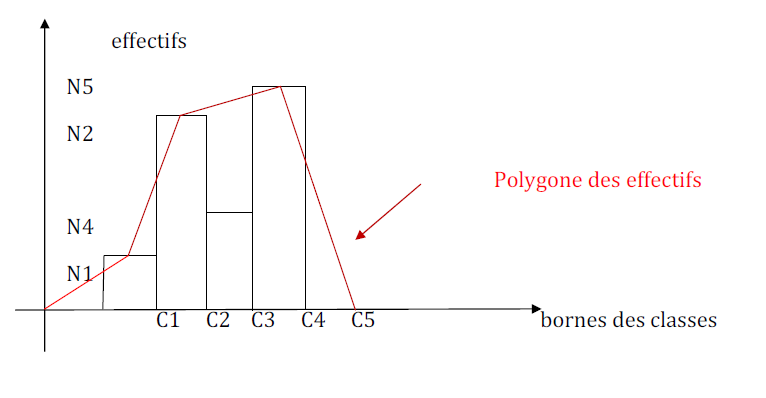
b) Polygone des fréquences :
Si les classes sont d'égale amplitude, le polygone des effectifs ou des fréquences est obtenu en joignant les milieux des bases supérieures des rectangles, puis en le fermant l'axe des abscisses en prenant une classe avant et une classe après toutes d'effectif nul
la surface située entre ce polygone et l'axe des abscisses est égale à l'aire totale de l'histogramme (somme des aires des rectangles)
Dans le cas où les classes n'ont même amplitude, on prendra soin à ce que la surface déterminée par ce polygone et l'axe des abscisses ait la même aire que l'histogramme
C) Courbe des effectifs cumulés (ou des fréquences cumulées) :
$-\ \ $ La courbe des effectifs cumulés croissants est obtenue en joignant les points dont les abscisses sont les bornes supérieures des classes et dont les ordonnées sont les effectifs cumulés croissants correspondants
Exemple :
$$\begin{array}{|c|c|c|c|} \hline &[2\;,\ 4[&[4\;,\ 6[&[6\;,\ 8[\\ \hline \text{Effectifs }n_{i}&2&3&5\\ \hline \text{Effectifs}&2&5&10\\ \text{cumulés}& & &\\ \hline \end{array}$$
La courbe des effectifs cumulés croissants joint les points $A(0\;,\ 2)$, $B(4\;,\ 2)$, $C(6\;,\ 5)$, $D(8\;,\ 10)$
$-\ \ $ La courbe des fréquences cumulées croissantes est obtenue en joignant par des segments les points dont les abscisses sont les bornes supérieures des classes et dont les ordonnées sont les fréquences cumulées croissantes correspondantes et en fermant cette courbe sur l'axe des abscisses.
$-\ \ $ La courbe des fréquences cumulées décroissantes est obtenue en joignant les points dont les abscisses sont les bornes inférieures des classes et dont les ordonnées sont les fréquences cumulées décroissantes correspondantes.
V. Détermination des quartiles :
1) Cas d'un caractère quantitatif discret :
On range les valeurs $x_{i}$ dans l'ordre croissant
$-\ \ $ Si l'effectif total $n=2p+1$ est impair, la $(p+1)^{ième}$ valeur est la médiane $M_{e}=\ :$ $M_{e}=xp+1$
$-\ \ $ Si l'effectif total $n=2p$ est pair et si la $p^{ième}$ et la $(p+1)^{ième}$ valeur sont égales alors $M_{e}=xp$
$-\ \ $ Si l'effectif total $n=2p$ est pair et $xp\neq xp+1$, on convient de prendre $M_{e}=\dfrac{x_{p}+x_{p+1}}{2}$
2) Cas d'un caractère quantitatif continu :
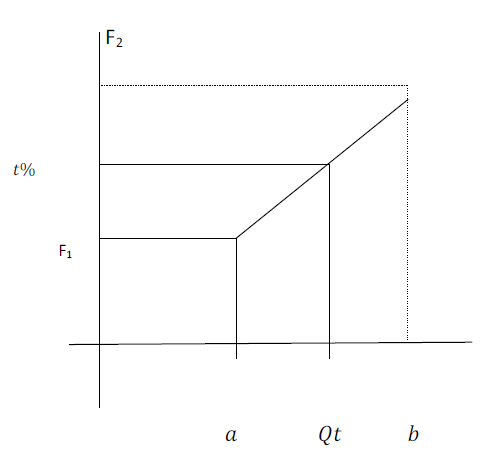
Pour calculer un quartile $\mathcal{Q}_{t}$ d'ordre $t\%$, on détermine la classe $[a\;,\ b[$ dans laquelle les fréquences cumulées croissantes atteignent $t\%.$
Si $F_{1}$ est la fréquence cumulée croissante de la classe $[c\;,\ b[$ qui précède $[a\;,\ b[$ et si $F_{2}$ est la fréquence cumulée croissante de la classe $[a\;,\ b[$, alors :
$\dfrac{t-F_{1}}{\mathcal{Q}_{t}-a}=\dfrac{F_{2}-F_{1}}{b-a}$ avec comme hypothèse l'équirépartition des valeurs de chaque classe.
On obtient :
$\mathcal{Q}_{t}=a+(b-a)\dfrac{t-F_{1}}{F_{2}-F_{1}}$
Si $t=25\%$ alors $\mathcal{Q}_{t}=\mathcal{Q}_{1}$, si $t=50\%$ alors $\mathcal{Q}_{t}=\mathcal{Q}_{2}$, si $t=75\%$, $\mathcal{Q}_{t}=\mathcal{Q}_{3}$
Le segment $[AB]$ correspond à la partie sur $[a\;,\ b]$ de la courbe des effectifs cumulés croissants
En exprimant de deux façons le coefficient directeur de $(AB)$, on a
$\dfrac{y_{M}-y_{A}}{x_{M}-x_{A}}=\dfrac{y_{B}-y_{A}}{x_{B}-x_{A}}$ ou encore
$\dfrac{t-F_{1}}{\mathcal{Q}_{t}-a}=\dfrac{F_{2}-F_{1}}{b-a}$ ou encore
$\dfrac{\mathcal{Q}_{t}-a}{b-a}=\dfrac{t-F_{1}}{F_{2}-F_{1}}$
Remarque :
$-\ \ $ Le quartile $\mathcal{Q}_{t}$ d'ordre $t\%$, graphiquement est l'abscisse du point $M$ d'ordonnée $t\%$, sur le diagramme des fréquences cumulées croissantes
$-\ \ M_{e}$ est l'abscisse du point d'intersection de la courbe des effectifs cumulés croissants et de la courbe des effectifs cumulés décroissants (ou abscisse du point d'ordonnée l'effectif moitié sur chacune de ces courbes)
$-\ \ M_{e}$ est l'abscisse du point d'intersection de le courbe des fréquences cumulées croissantes et de la courbe des fréquences cumulées décroissantes (ou abscisse du point d'ordonnées $50\%$ sur chacune de ces courbes)
Série statistique double
L'étude simultanée de deux caractères $X$ et $Y$ quantitatifs sur une même population d'effectif total $n$, donne une série statistique double qui est l'ensemble des triplets $\left(x_{i}\;,\ y_{j}\;,\ n_{ij}\right)$, $i$ allant de $1$ à $p$, $j$ allant de $1$ à $q$, $x_{1}$, $x_{2}$, $\ldots$, $x_{p}$ étant les valeurs du caractère $X$, $y_{1}$, $y_{2}$, $\ldots$, $y_{q}$ étant les valeurs du caractère $Y$, $n_{ij}$ étant l'effectif du couple $\left(x_{i}\;,\ y_{j}\right)$ ou le nombre de fois que le couple $\left(x_{i}\;,\ y_{j}\right)$ est observé
Remarque :
$X$ et $Y$ peuvent être tous les deux quantitatifs discrets ou tous les deux quantitatifs continus, l'un quantitatif discret et l'autre quantitatif continu.
Auteur:
Ka, Faye & Mbengue

Ajouter un commentaire