Orthogonalité et produit scalaire dans l'espace - 1er S
Classe:
Première
I. Droites orthogonales
Définition :
Deux droites $\mathcal{D}$ et $\mathcal{D'}$ de l'espace $\mathcal{E}$ sont dites orthogonales si leurs parallèles $\mathcal{D}_{A}$ et $\mathcal{D'}_{A}$ menées par un point quelconque $A$ de $\mathcal{E}$ sont perpendiculaires.
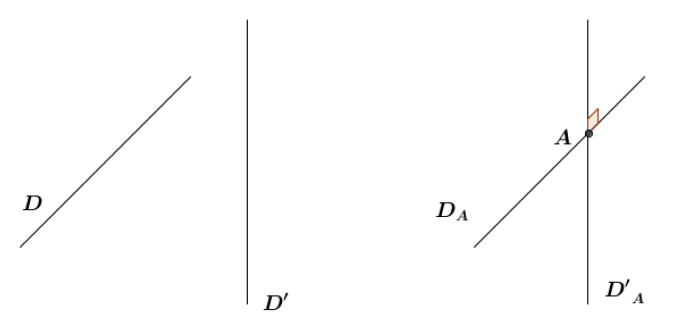
Remarques :
1) Nous admettrons que cette définition ne dépend pas du choix du point $A.$
Cela revient à admettre que la distance est invariante par translation dans $\mathcal{E}.$
2) Deux droites de $\mathcal{E}$ peuvent être orthogonales et non coplanaires :
Elles n'ont alors aucun point commun.
Théorème 1 :
1) Si deux droites sont orthogonales, toute parallèle à l'une est orthogonale à l'autre.
2) Si deux droites sont parallèles, toute orthogonale à l'une est orthogonale à l'autre.
3) Deux droites sont orthogonales si et seulement si elles sont parallèles à deux droites orthogonales.
Démonstration :
1) Supposons que $\mathcal{D}\perp\mathcal{D'}$ et $\Delta\parallel\mathcal{D}.$
Soient $\mathcal{D}_{A}$ et $\mathcal{D'}_{A}$ les parallèles menées par un point $A$ à $\mathcal{D}$ et $\mathcal{D'}.$
On a $\mathcal{D}_{A}\perp\mathcal{D'}_{A}.$
La parallèle $\Delta_{A}$ à $\Delta$ passant par $A$ n'est autre que $\mathcal{D}_{A}$ car $\Delta\parallel\mathcal{D}_{A}$ (voir Axiome d'EUCLIDE).
Donc $\Delta_{A}\parallel\mathcal{D'}_{A}$, d'où $\Delta\perp\mathcal{D'}.$
2) Supposons que $\mathcal{D}\parallel\mathcal{D'}\text{ et }\Delta\perp\mathcal{D}.$
Alors $\mathcal{D}_{A}=\mathcal{D'}_{A}.$
Or $\Delta_{A}\perp\mathcal{D}_{A}$, donc $\Delta_{A}\perp\mathcal{D'}_{A}$, d'où $\Delta\perp\mathcal{D'}.$
3) « $\Rightarrow$ » : Si $\mathcal{D}\parallel\mathcal{D'}$, alors leurs parallèles $\mathcal{D}_{A}$ et $\mathcal{D'}_{A}$ sont orthogonales par définition.
« $\Leftarrow$ » : Réciproquement, supposons qu'il existe deux droites $\Delta$ et $\Delta'$ telles que :$$\mathcal{D}\parallel\Delta\;, \ \mathcal{D'}\parallel\Delta'\text{ et }\Delta\perp\Delta'.$$
Alors, $\mathcal{D}_{A}=\Delta_{A}$ et $\mathcal{D'}_{A}=\Delta'_{A}.$
Par hypothèse, on a $\Delta_{A}\perp\Delta'_{A}$, d'où $\mathcal{D_{A}}\perp\mathcal{D'}_{A}$, donc $\mathcal{D}\perp\mathcal{D'}.$
Remarques :
$\bullet$ Attention, dans l'espace $\mathcal{D}\perp\mathcal{D'}$ et $\mathcal{D}\perp\mathcal{D''}$ n'entraîne pas $\mathcal{D'}\parallel\mathcal{D''}.$
Alors que dans le plan ce résultat est vrai.
Par exemple dans le cube ci-dessous :
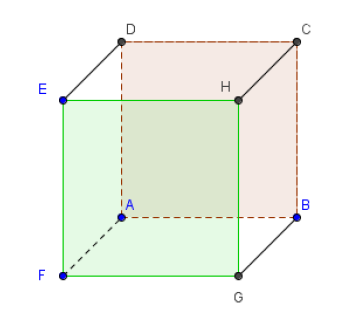
Les droites $(DE)$ et $(FG)$ sont orthogonales à la droite $(EF)$ et pourtant $(DE)$ et $(FG)$ ne sont pas parallèles !
$\bullet$ Bien faire la nuance entre droites orthogonales et droites perpendiculaires :
On parle de droites orthogonales pour des droites qui n'ont pas de point d'intersection :
Elles ne sont pas coplanaires.
Par contre, dans l'espace, perpendiculaires signifie orthogonales et sécantes.
II. Droite orthogonale à un plan
Définition :
Une droite est dite orthogonale à un plan si elle est orthogonale à toute droite de ce plan.
Remarque :
Si une droite $\mathcal{D}$ et un plan $\mathcal{P}$ sont orthogonaux, alors ils sont sécants.
En effet, si $\mathcal{D}$ était parallèle à $\mathcal{P}$ elle serait parallèle à une droite $\Delta$ de $\mathcal{P}.$
Or $\mathcal{D}$ est supposée être orthogonale à toute droite $\Delta$ de $\mathcal{P}.$
$\mathcal{D}$ et $\Delta$ seraient donc à la fois parallèles et orthogonales, ce qui est absurde.
Théorème Fondamental :
Une droite $\Delta$ est orthogonale à un plan $\mathcal{P}$ si et seulement si $\Delta$ est orthogonale à deux droites sécantes de $\mathcal{P}.$
Démonstration :
« $\Rightarrow$ » : C'est évident, car si $\Delta$ est orthogonale à toutes les droite de $\mathcal{P}$, elle est évidemment orthogonale à deux droites sécantes de $\mathcal{P}.$
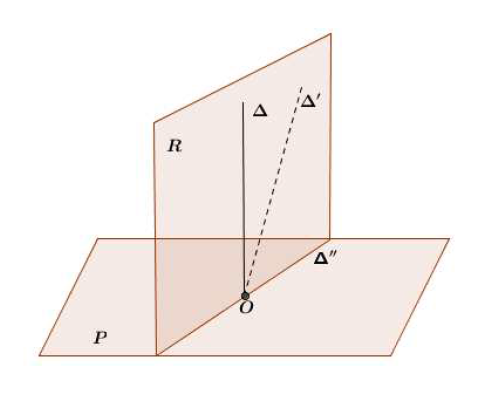
« $\Rightarrow$ » : Soient $\Delta_{1}$ et $\Delta_{2}$ deux droites sécantes en $O$ du plan $\mathcal{P}.$
Quitte à remplacer $\Delta$ par une de ses parallèles, on peut supposer que $\Delta$ est orthogonale à $\Delta_{1}$ et $\Delta_{2}$ en $O.$
Dans le plan $\mathcal{P}$, menons par $O$ une droite $\mathcal{D}$ quelconque distincte de $\Delta_{1}$ et $\Delta_{2}.$
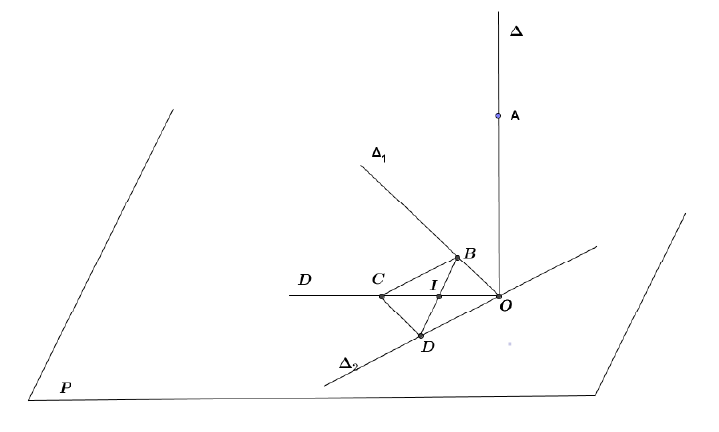
On considère sur les droites $\Delta$ et $\mathcal{D}$ respectivement deux points distincts de $O$ notés $A$ et $C.$
On considère sur $\Delta_{1}$ et $\Delta_{2}$ les points $B$ et $D$ tels que $OBCD$ soit un parallélogramme de centre $I.$
D'après le théorème de la médiane dans la triangle $OBD$, on a :
$$OB^{2}+OD^{2}=2OI^{2}+\dfrac{BD^{2}}{2}\quad (1)$$
Et d'après ce même théorème dans le triangle $ABD$, on a :
$$AB^{2}+AD^{2}=2AI^{2}+\dfrac{BD^{2}}{2}\quad(2)$$
Les triangles $AOB$ et $AOD$ étant rectangles en $O$ par hypothèse, on a en utilisant le théorème de PYTHAGORE :
$$AB^{2}=AO^{2}+OB^{2}\text{ et }AD^{2}=AO^{2}+OD^{2}.$$
En substituant ces expressions dans (2), on obtient :
$$2AO^{2}+OB^{2}+OD^{2}=2AI^{2}+\dfrac{BD^{2}}{2}$$
Puis en tenant compte de (1) :
$$2AO^{2}+2OI^{2}+\dfrac{BD^{2}}{2}=2AI^{2}+\dfrac{BD^{2}}{2}$$
En simplifiant, il vient alors : $$AO^{2}+OI^{2}=AI^{2}.$$
On en conclut que $\Delta$ est orthogonale en $O$ à $\mathcal{D}$ :
Ainsi $\Delta$ est orthogonale à n'importe quelle droite $\mathcal{D}$ de $\mathcal{P}.$ C.Q.F.D.
Les théorèmes qui suivent sont des conséquences du théorème fondamental.
Théorème 2 :
Lorsque deux droites sont parallèles, tout plan orthogonal à l'une est orthogonal à l'autre.
Démonstration :
Soient deux droites parallèles $\mathcal{D}$ et $\mathcal{D'}$ et $\mathcal{P}$ un plan orthogonal à $\mathcal{D}.$
Soient $\mathcal{X}$ et $\mathcal{X'}$ deux droites sécantes du plan $\mathcal{P}.$
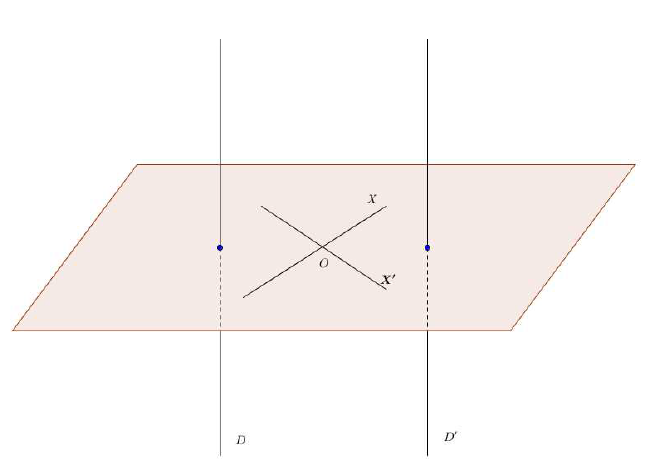
$\mathcal{D}\perp\mathcal{X}\Rightarrow\mathcal{D'}\perp\mathcal{X}$ (d'après le théorème 1, 1).
$\mathcal{D}\perp\mathcal{X'}\Rightarrow\mathcal{D'}\perp\mathcal{X'}$ (d'après le théorème 1, 1).
$\mathcal{D'}$ est donc orthogonale à deux droites séantes $\mathcal{X}$ et $\mathcal{X'}$ du plan $\mathcal{P}$, d'où $\mathcal{D'}\perp\mathcal{P}$, d'après le théorème fondamental.
Théorème 3 :
Lorsque deux plans sont parallèles, toute droite orthogonale à l'une est orthogonale à l'autre.
Démonstration :
Supposons que $\mathcal{P}\parallel\mathcal{P'}$ et $\Delta\perp\mathcal{P}.$
Soient $\mathcal{D_{1}}$ et $\mathcal{D_{2}}$ deux droites sécantes en $A$ et incluses dans $\mathcal{P}.$
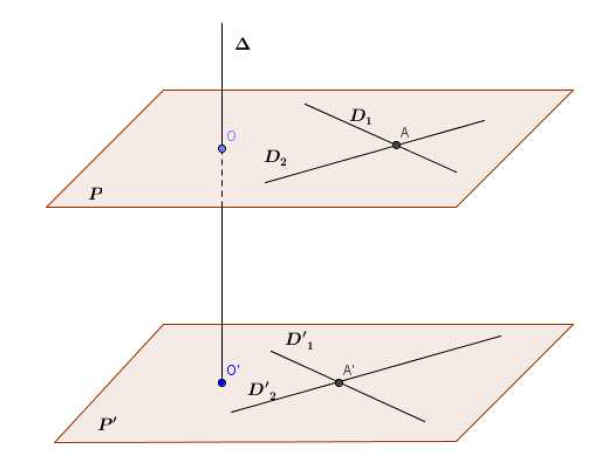
Leurs parallèles et $\mathcal{D'_{1}}$ et $\mathcal{D'_{2}}$, menées par un point $A'$ de $\mathcal{P'}$, appartiennent à $\mathcal{P'}$.
$\Delta$ étant orthogonale à $\mathcal{P}$ est orthogonale à $\mathcal{D_{1}}$, par définition, donc à $\mathcal{D'_{1}}$ (d'après le théorème 1, 2).
De même, $\Delta\perp\mathcal{D_{2}}\Rightarrow\Delta\perp\mathcal{D'_{2}}.$
Par conséquent, $\Delta$ est orthogonale à $\mathcal{P'}$ puisqu'elle est orthogonale à deux droites sécantes de $\mathcal{P'}.$
Théorème 4 :
Par un point donné $\mathcal{P}$, on peut mener un plan $\mathcal{P}$ et un seul orthogonal à une droite donnée $\Delta.$
Démonstration :
a) Existence
$1^{er}$ cas : Le point $O$ appartient à la droite $\Delta$
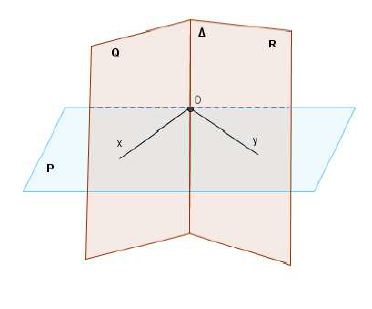
Soient $\mathcal{Q}$ et $\mathcal{R}$ deux plans sécants suivant la droite $\Delta.$
Dans le plan $\mathcal{Q}$, il existe une droite unique passant par $O$ et perpendiculaire à $\Delta$ (Théorème de géométrie plane).
Notons-la $Ox.$
De même, dans le plan $\mathcal{R}$, une unique droite passant par $O$ et perpendiculaire à $\Delta$ que nous noterons $Oy.$
Le plan $\mathcal{P}=(Ox\;,\ Oy)$ est alors perpendiculaire à $\Delta.$
$2^{ième}$ cas : Le point $O$ n'appartient pas à la droite $\Delta$
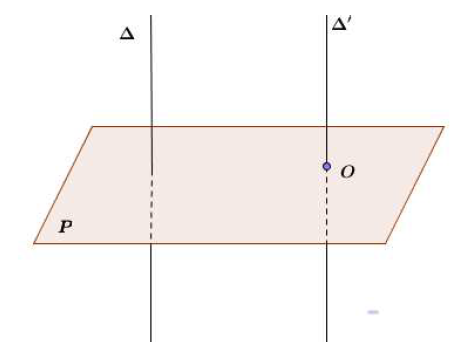
Soit $\Delta'$ la parallèle à $\Delta$ passant par $O.$
D'après le premier cas, il existe un seul plan $\mathcal{P}$ passant par $O$ et orthogonal à $\Delta'.$
$\Delta$ étant parallèle à $\Delta'$ et $\mathcal{P}$ orthogonal à $\Delta'$, il en résulte (théorème 2) que $\mathcal{P}$ est orthogonal à $\Delta.$
En outre, $\mathcal{P}$ passe par $O.$
b) Unicité
Supposons qu'il existe deux plans $\mathcal{P_{1}}$ et $\mathcal{P_{2}}$ passant par $O$ orthogonaux à $\Delta.$
Comme ces deux plans sont distincts et ont un point commun, ils sont sécants suivant une droite $\Delta'.$
Soit $\mathcal{P}$ le plan défini par $\Delta_{0}$ et $\Delta'$, où $\Delta_{0}$ est la parallèle à $\Delta$ passant par $O.$
$\mathcal{P}$ coupe $\mathcal{P_{2}}$ suivant une droite $\Delta''$ passant par $O.$
$\Delta_{0}$ est orthogonale à $\mathcal{P_{2}}$ car $\Delta\parallel\Delta_{0}$ et $\Delta\perp\mathcal{P_{2}}$ (cf. théorème 2).
Donc $\Delta_{0}\perp\Delta''$ et $\Delta_{0}\perp\Delta'$ (car $\Delta'\in\mathcal{P_{2}}).$
Or, $\Delta_{0}$, $\Delta'$ et $\Delta''$ sont toutes trois des droites de $\mathcal{P}$ et $\Delta'$ et $\Delta''$ sont sécantes en $O$ :
d'où une contradiction (deux droites d'un même plan orthogonales à une même troisième doivent être parallèles).
Conséquence :
Deux plans orthogonaux à une même droite sont parallèles.
En effet, si deux plans $\mathcal{P_{1}}$ et $\mathcal{P_{2}}$ étaient orthogonaux à une même droite $\Delta$ et sécants, soit $O$ un point de $\mathcal{P_{1}}\cap\mathcal{P_{2}}.$
Par $O$ passeraient deux plans $\mathcal{P_{1}}$ et $\mathcal{P_{2}}$ orthogonaux à $\Delta$, ce qui contredit le théorème 4.
Théorème 5 :
Par un point donné $O$, passe un plan $\mathcal{P}$ et un seul orthogonal à une droite donnée.
Démonstration :
$1^{er}$ cas : $O\in\mathcal{P}$
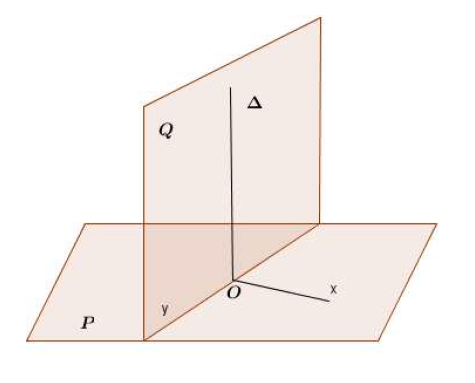
Soit $Ox$ une droite quelconque de $\mathcal{P}.$
D'après le théorème 4, il existe un plan unique $\mathcal{Q}$ passant par $O$ et perpendiculaire à $Ox.$
Ce plan $\mathcal{Q}$ coupe $\mathcal{P}$ suivant une droite $Oy.$
Dans ce plan $\mathcal{Q}$, soit $\Delta$ la perpendiculaire à $Oy$ passant par $O.$
$\Delta$ est par construction perpendiculaire aux deux droites sécantes $Ox$ et $Oy$ du plan $\mathcal{P}$, donc $\Delta\perp\mathcal{P}.$
Supposons qu'il existe une autre droite $\Delta'$ distincte de $\Delta$ et perpendiculaire en $O$ au plan $\mathcal{P}.$ (cf. Figure ci-dessous).
$\Delta$ et $\Delta'$ détermineraient un plan $\mathcal{R}$ qui couperait $\mathcal{P}$ suivant une droite $\Delta''$ passant par $O.$
Dans ce plan $\mathcal{R}$, on aurait :
$\Delta''\perp\Delta\text{ et }\Delta''\perp\Delta'$ :
Ceci est absurde car $\Delta$ et $\Delta'$ sont deux droites sécantes (en $O$) du plan $\mathcal{R}.$
$2^{ième}$ cas : $O\not\in\mathcal{P}$
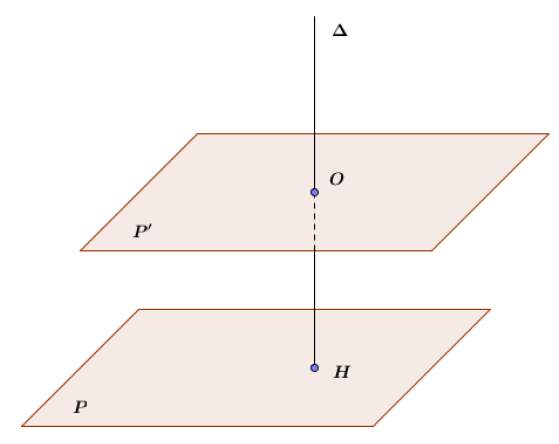
Soit $\mathcal{P'}$ le plan passant par $O$ et parallèle à $\mathcal{P}.$
D'après le $1^{er}$ cas, il existe une unique droite $\Delta$ passant par $O$ et parallèle à $\mathcal{P'}.$
$\Delta$ est perpendiculaire à $\mathcal{P}$ (d'après le théorème 3).
Toute autre droite perpendiculaire à $\mathcal{P}$ est perpendiculaire à $\mathcal{P'}$, donc est confondue avec $\Delta.$
Conséquence :
Deux droites orthogonales à un même plan sont parallèles.
En effet, si $\mathcal{D}$ et $\mathcal{D'}$ sont perpendiculaires à $\mathcal{P}$ en $A$ et $A'$ respectivement, soit $\Delta_{1}$ la parallèle à $\mathcal{D}$ passant par $A'.$
Alors $\Delta_{1}$ est perpendiculaire au plan $\mathcal{P}$ (d'après le théorème 2), donc confondue avec $\mathcal{D'}$ (puisqu'il n'existe qu'une seule perpendiculaire en $A'$ à $\mathcal{P}).$
En d'autres termes, $\mathcal{D}$ et $\mathcal{D'}$ sont parallèles.
Les théorèmes $4$ et $5$ nous permettent de définir la notion de projection orthogonale dans l'espace.
Il y a deux cas :
Définition 1 :
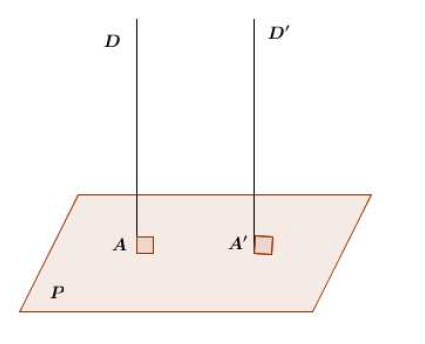
Soit $M$ un point quelconque de l'espace et $\mathcal{P}$ un plan donné.
Il existe (d'après le théorème $5$) une droite $\mathcal{D}_{M}$ et une seule passant par $M$ et orthogonale à $\mathcal{P}.$
$\mathcal{D}_{M}$ perce $\mathcal{P}$ en un point $M'.$
$M'$ est, par définition le projeté orthogonal du point $M$ sur le plan $\mathcal{P}.$
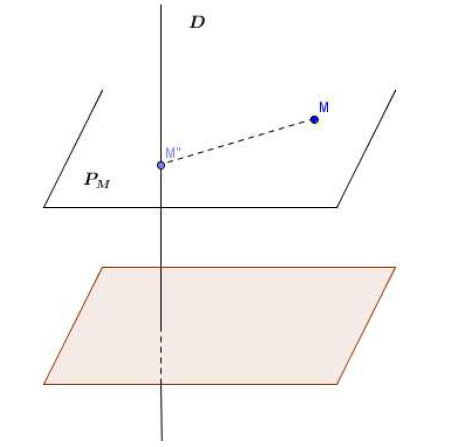
Définition 2 :
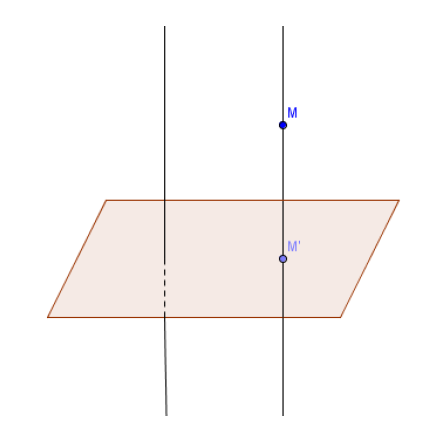
Soit $M$ un point quelconque de l'espace et $\mathcal{D}$ une droite donné.
Il existe (d'après le théorème $4$) un plan $\mathcal{P}_{M}$ et un seul passant par $M$ et perpendiculaire à $\mathcal{D}.$
$\mathcal{P}_{M}$ coupe $\mathcal{D}$ en un point $M''.$
$M''$ est, par définition le projeté orthogonal du point $M$ sur la droite $\mathcal{D}.$
Nous définissons également la notion très importante de plan médiateur :
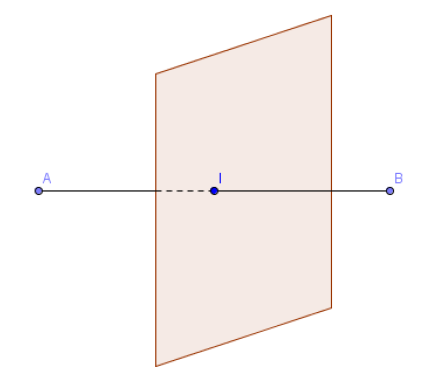
Définition 3 :
Soient $A$ et $B$ deux points distincts de l'espace.
Le plan médiateur du segment $[AB]$ est le plan passant par $I$ milieu de $[AB]$ et orthogonal à $(AB).$
Théorème 6 :
Le plan médiateur du segment $[AB]$ est l'ensemble des points de l'espace équidistants de $A$ et $B.$
Démonstration :
Il est clair que le point $I$ appartient au plan médiateur de $[AB]$ et que $IA=IB.$
Soit $M$ un point du plan médiateur de $[AB]$ distinct de $I.$
$M$, $A$, et $B$ définissent un plan (car, par définition, le plan médiateur de $[AB]$ n'a d'intersection avec la droite $(AB)$ que le point $I$, donc $M$, $A$ et $B$ sont non alignés).
Plaçons-nous dans le plan $(MAB).$
$I$ appartient à ce plan et on a $(MI)\perp (AB)$ (car $(AB)$ est orthogonal par définition à toutes les droites du plan médiateur de $[AB]).$
Donc $(MI)$ est la médiatrice de $[AB]$ dans le plan $(MAB).$
D'où : $MA=MB.$
Réciproquement, supposons que : $MA=MB$ et que $M$ ne soit pas confondu avec $I.$
Alors dans le plan $(MAB)$, la droite $(MI)$ est la médiatrice du segment $[AB]$, donc $(MI)$ est orthogonale au segment $[AB].$
Exercice :
Soit $G$ barycentre de ${(A\;,\ 2)\;,\ (B\;,\ 1)\;,\ (C\;,\ -1)}$ et $K$ barycentre de ${(A\;,\ 2)\;,\ (B\;,\ -1)\;,\ (C\;,\ 1)}.$
Déterminer l'ensemble des points $M$ de l'espace tels que
$$\|2\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}\|=\|2\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}\|$$
Réponse :
On trouve le plan médiateur de $[GK].$
IV. Vecteur normal à un plan
Définition :
On appelle vecteur normal à un plan $\mathcal{P}$ tout vecteur directeur d'une droite $\mathcal{D}$ orthogonale à $\mathcal{P}.$
Théorème 7 :
Deux plans sont parallèles si et seulement si ils admettent des vecteurs normaux colinéaires.
Démonstration :
« $\Rightarrow$ » : Supposons que $\mathcal{P}$ et $\mathcal{P'}$ soient parallèles.
Soient $\vec{n}$ et $\mathcal{n4}$ deux vecteurs directeurs de $\mathcal{D}$ et $\mathcal{D'}$ orthogonales à $\mathcal{P}$ et $\mathcal{P'}$ respectivement.
On a : $(\mathcal{D}\perp\mathcal{P}\text{ et }\mathcal{P}\parallel\mathcal{P'})\Rightarrow (\mathcal{D}\perp\mathcal{P'})$ (d'après le théorème 3).
Et : $(\mathcal{D}\perp\mathcal{P'}\text{ et }\mathcal{D'}\perp\mathcal{P'})\Rightarrow (\mathcal{D}\parallel\mathcal{D'})$ (d'après la conséquence du théorème 5).
$\vec{n}\text{ et }\vec{n'}$ sont donc colinéaires.
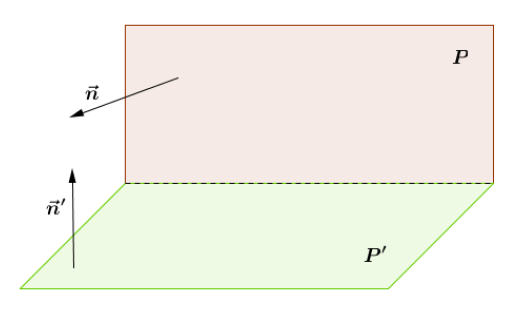
« $\Leftarrow$ » : Soient $\vec{n}$ et $\vec{n'}$ deux vecteurs normaux à $\mathcal{P}$ et $\mathcal{P'}$ tels que $\vec{n}$ et $\vec{n'}$ soient colinéaires.
Il existe deux droites $\mathcal{D}$ et $\mathcal{D'}$ de vecteurs directeurs respectifs $\vec{n}$ et $\vec{n'}.$
$\mathcal{D}$ et $\mathcal{D'}$ sont alors parallèles.
Et puisque $\mathcal{D'}\perp\mathcal{P'}$, on a $\mathcal{D}\perp\mathcal{P'}$ (théorème 2).
D'autre part, $(\mathcal{D}\perp\mathcal{P}\text{ et }\mathcal{D}\perp\mathcal{P'})\Rightarrow(\mathcal{P}\parallel\mathcal{P'})$ (conséquence du théorème 4).
V. Produit scalaire dans l'espace
Définition :
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs de l'espace et $O$ un point donné.
Il existe (d'après l'Axiome d'EUCLIDE) des points $A$ et $B$ (uniques) tels que :
$$\overrightarrow{OA}=\vec{u}\text{ et }\overrightarrow{OB}=\vec{v}$$
On appelle alors produit scalaire de $\vec{u}$ et $\vec{v}$ le produit scalaire $\overrightarrow{OA}\cdot\overrightarrow{OB}=\overline{OA}\times\overline{OH}$ dans le plan $(OAB)$ ($H$ étant le projeté orthogonal du point $B$ sur la droite $(OA).$
Nous admettrons que cette définition est indépendante du point $O$ choisi.
Théorème 8 :
1) Pour tous vecteurs $\vec{u}$ et $\vec{v}$ de l'espace et tout réel $k$, on a :
a) $\vec{u}\cdot\vec{v}=\vec{v}\cdot\vec{u}$ b) $\vec{u}\cdot(k\vec{v})=k(\vec{u}\cdot\vec{v})$
2) Pour tous vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ de l'espace, on a :
$\vec{u}\cdot(\vec{v}+\vec{w})=\vec{u}\cdot\vec{v}+\vec{u}\cdot\vec{w}$
Nous admettrons que ces propriétés sont vraies même si $\vec{u}$, $\vec{v}$ et $\vec{w}$ ne sont pas coplanaires.
Définition :
On appelle carré scalaire du vecteur $\vec{u}$ le réel $\vec{u}\cdot\vec{u}$ noté $\vec{u}^{2}.$
Théorème 9 :
Pour tout vecteur $\vec{u}$, on a :
$\vec{u}\cdot\vec{u}\geq 0\text{ et }\vec{u}^{2}=0\text{ si et seulement si }\vec{u}=\vec{0}.$
Définition :
Dans l'espace, la norme du vecteur $\vec{u}$ est, par définition $\|\vec{u}\|=\sqrt{\vec{u}^{2}}.$
Théorème 10 :
1) Pour tout vecteur $\vec{u}$, on a :
$\|\vec{u}\|=0\;\Leftrightarrow\;\vec{u}=\vec{0}.$
2) $\|\overrightarrow{AB}\|=AB$
3) $\forall\lambda\in\mathbb{R}\;,\ \|\lambda\vec{u}\|=|\lambda|\|\vec{u}\|.$
4) $|\vec{u}\cdot\vec{v}|\leq\|\vec{u}\|\times\|\vec{v}\|$ (inégalité de Cauchy-Schwarz)
5) $\|\vec{u}+\vec{v}\|\leq\|\vec{u}\|+\|\vec{v}\|$ (inégalité triangulaire)
6) $\|\vec{u}+\vec{v}\|^{2}=\|\vec{u}\|^{2}+2\vec{u}\cdot\vec{v}+\|\vec{v}\|^{2}$
7) $\|\vec{u}-\vec{v}\|^{2}=\|\vec{u}\|^{2}-2\vec{u}\cdot\vec{v}+\|\vec{v}\|^{2}$
8) $(\vec{u}+\vec{v})\cdot(\vec{u}-\vec{v})=\|\vec{u}\|^{2}-\|\vec{v}\|^{2}$
Démonstration :
Les trois premiers résultats sont des conséquences de la définition de la norme.
Les suivantes se démontrent, comme dans le plan en prenant des représentants des vecteurs et en utilisant les propriétés du produit scalaire admises au théorème 8.
Définition :
Deux vecteurs $\vec{u}$ et $\vec{v}$ sont dits orthogonaux si et seulement si $\vec{u}\cdot\vec{v}=0$
N.B
Comme dans le plan, on note alors $\vec{u}\perp\vec{v}.$
Propriétés :
1) $\vec{u}\perp\vec{v}\Rightarrow\forall\lambda\in\mathbb{R}\;,\ \forall\mu\in\mathbb{R}\;,\ (\lambda\vec{u})\perp(\mu\vec{v})$
2) Deux droites $\mathcal{D}$ et $\mathcal{D'}$ sont orthogonales si et seulement si il existe un vecteur directeur $\vec{u}$ de $\mathcal{D}$ et un vecteur directeur $\vec{u'}$ de $\mathcal{D'}$ tel que $\vec{u}\perp\vec{u'}.$
3) Une droite $\mathcal{D}$ est orthogonale à un plan $\mathcal{P}$ si et seulement si il existe un vecteur directeur $\vec{u}$ de $\mathcal{D}$ et deux vecteurs directeurs non colinéaires $\vec{u'}$ et $\vec{u''}$ de $\mathcal{P}$ tels que :
$\vec{u}\perp\vec{u'}\text{ et }\vec{u}\perp\vec{u''}.$
4) L'ensemble des points $M$ de l'espace tels que $\overrightarrow{AM}\perp\vec{n}$ est le plan passant par $A$ et de vecteur normal $\vec{n}.$
Démonstration :
Ces propriétés sont des conséquences de la définition de l'orthogonalité de deux vecteurs ainsi que des résultats déjà établis sur l'orthogonalité d'une droite et d'un plan ou celle de deux droites.
VI. Plans perpendiculaires
Définition :
Deux plan $\mathcal{P}$ et $\mathcal{P'}$ sont dits perpendiculaires s'il existe un vecteur $\overrightarrow{n}$ de $\mathcal{P}$ et un vecteur normal $\vec{n'}$ de $\mathcal{P'}$ tels que $\vec{n}\perp\vec{n'}.$
Remarque :
Deux plans perpendiculaires sont sécants.

En effet, avec les notations précédentes, si $\mathcal{P}$ était parallèle à $\mathcal{P'}$, $\vec{n}$ et $\vec{n'}$ seraient colinéaires.
Or $\vec{n}$ et $\vec{n'}$ sont non nuls et orthogonaux : contradiction.
Théorème 11 :
Deux plan sont perpendiculaires si et seulement si l'un contient une droite orthogonale à l'autre.
Démonstration :
« $\Rightarrow$ » : Supposons que $\mathcal{P}$ et $\mathcal{P'}$ soient perpendiculaires et soit $\vec{n}$ et $\vec{n'}$ des vecteur normaux respectifs à $\mathcal{P}$ et $\mathcal{P'}.$
Soit $A$ un de leurs points communs $(A\in\mathcal{P}\cap\mathcal{P'}).$
Soit $\mathcal{D}$ la droite définie par $A$ et $\vec{n}$, $\mathcal{D'}$ la droite définie par $A$ et $\vec{n'}.$
Alors les droites $\mathcal{D}$ et $\mathcal{D'}$ sont orthogonales.
Soit $\pi$ le plan $(\mathcal{D}\;,\ \mathcal{D'}).$
$\pi$ coupe $\mathcal{P}$ suivant une droite $\delta$ passant par $A.$
$\mathcal{D}\perp\mathcal{P}$, donc $\mathcal{D}\perp\delta.$
$\mathcal{D}\perp\delta$, $\mathcal{D}\perp\mathcal{D'}$ et toutes trois sont coplanaires et passent par $A$ : alors $\mathcal{D'}=\delta.$
Donc $\mathcal{D'}\perp\mathcal{P}\text{ et }\mathcal{D'}\perp\mathcal{P'}.$
« $\Leftarrow$ » : Supposons que $\mathcal{P}$ contienne une droite $\Delta$ orthogonale à $\mathcal{P'}.$
Soit $\vec{u}$ un vecteur directeur de $\Delta.$
Alors $\vec{u}$ est un vecteur normal à $\mathcal{P'}.$
Soit $\vec{n}$ un vecteur normal à $\mathcal{P}.$
Alors $\vec{n}$ est orthogonal à tout vecteur de la direction de $\mathcal{P}$, donc en particulier à $\overrightarrow{u}.$
Remarques :
1) Si $\mathcal{P}\perp\mathcal{P'}$, toute droite $\mathcal{D}$ orthogonale à $\mathcal{P}$ et toute droite $\mathcal{D'}$ orthogonale à $\mathcal{P'}$ sont orthogonales.
2) Par contre toute droite de $\mathcal{P}$ n'est pas nécessairement orthogonale à toute droite de $\mathcal{P'}.$
VII. Repères orthonormés de l'espace
Définition :
Une base $(\vec{i}\;,\ \vec{j}\;,\ \vec{k})$ de l'espace est dite orthonormée si et seulement si :
$$\vec{i}\cdot\vec{j}=\vec{j}\cdot\vec{k}=\vec{k}\cdot\vec{i}=\vec{0}\text{ et }\|\vec{i}\|=\|\vec{j}\|=\|\vec{k}\|=1.$$
Un repère orthonormé de $\mathcal{E}$ est un quadruplet $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ où $O$ est un point de $\mathcal{E}$ et $(\vec{i}\;,\ \vec{j}\;,\ \vec{k})$ une base orthonormée.
Théorème 12 :
Soit $(O\;,\ \vec{i}\;,\ \vec{j}\;,\ \vec{k})$ un repère orthonormé de l'espace, $\vec{u}$ et $\vec{u'}$ les vecteurs de coordonnées respectives $(x\;,\ y\;,\ z)$ et $(x'\;,\ y'\;,\ z')$ dans ce repère.
Alors on a :
$$\vec{u}\cdot\vec{u'}=xx'+yy'+zz'\text{ et }\|\vec{u}\|=\sqrt{x^{2}+y^{2}+z^{2}}$$
Démonstration :
D'après les propriétés du produit scalaire vues au théorème 8, on a :
$\begin{array}{rcl}\vec{u}\cdot\vec{v}&=&(x\vec{i}+y\vec{j}+z\vec{k})\cdot(x'\vec{i}+y'\vec{j}+z'\vec{k})\\ \\&=&(xx')\vec{i}^{2}+(yy')\vec{j}^{2}+(zz')\vec{k}^{2}+(xy'+yx')\vec{i}\cdot\vec{j}+(yz'+zy')\vec{j}\cdot\vec{k}+(xz'+zx')\vec{k}\cdot\vec{i}\end{array}$
D'où la première égalité, puisque $(\vec{i}\;,\ \vec{j}\;,\ \vec{k})$ est une base orthonormée.
La deuxième égalité provient de la relation $\|\vec{u}\|=\sqrt{\vec{u}^{2}}.$
Corollaire :
1) Soit $\overrightarrow{u}$ et deux vecteurs de coordonnées respectives $(x\;,\ y\;,\ z)$ et $(x'\;,\ y'\;,\ z')$ dans la base orthonormée $\mathcal{B}.$
Alors : $$\vec{u}\perp\vec{u'}\Leftrightarrow xx'+zz'=0.$$
2) Soient $A$ et $B$ deux points de l'espace de coordonnées $(x_{A}\;,\ y_{A}\;,\ z_{A})\text{ et }(x_{B}\;,\ y_{B}\;,\ z_{B})$ dans un repère orthonormé $\mathcal{R}.$
Alors, on a :
$$\|\overrightarrow{AB}\|=\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}+\left(z_{B}-z_{A}\right)^{2}}$$
Auteur:
Ka, Faye & Mbengue

Ajouter un commentaire