Série d'exercices : Les polygones - Quadrilatères et Aires 6e
Classe:
Sixième
Exercice 1
1) Construire un trapèze $ABCD$ connaissant les bases : $AB=5\;cm\;;\ CD=7\;cm.$ Le coté oblique $AD=3\;cm\ $ et $\ mes\;\widehat{BAD}=120^{\circ}.$
2) Après avoir mesuré la hauteur du trapèze, calculer l'aire de $ABCD.$
Exercice 2
1) Construire un trapèze rectangle $ABCD$ tel que :
$$mes\;\widehat{A}=mes\;\widehat{B}=90^{\circ}\;;\ AB=4\;cm\;;\ BC=5\;cm\ \text{ et }\ AD=6\;cm$$
$$mes\;\widehat{A}=mes\;\widehat{B}=90^{\circ}\;;\ AB=4\;cm\;;\ BC=5\;cm\ \text{ et }\ AD=6\;cm$$
2) Après avoir mesuré $CD$, calculer l'aire et le périmètre de $ABCD.$
Exercice 3
1) Construire un trapèze isocèle $MNPQ$ connaissant les bases : $MN=4.5\;cm\;;\ PQ=8.5\;cm$ et le coté oblique mesure $4\;cm.$
2) Après avoir mesuré la hauteur du trapèze, calculer l'aire de $MNPQ.$
Exercice 4
1) Construire un parallélogramme $ABCD$ tel que $AB=5\;cm\ $ et $\ BC=4\;cm.$
2) Placer les points $I$ et $J$ milieux respectifs des segments $[AB]\ $ et $\ [BC].$
3) La parallèle à $(BC)$ passant par $I$ coupe $[DC]$ en $K.$
4) La parallèle à $(AB)$ passant par $J$ coupe $[AD]$ en $H.$
5) Soit $L$ le point commun à $(HJ)\ $ et $\ (IK).$
6) Quelle est la nature des quadrilatères : $DKLH\;,\ KCJL\;,\ ILJB\ $ et $\ AILH.$
Exercice 5
1) Construire un rectangle $RECT$ tel que : $RE=4\;cm\ $ et $\ RC=5.5\;cm.$
2) Construire les axes de symétrique de $RECT.$
3) Calculer l'aire de $RECT.$
Exercice 6
1) Construire un carré $CARE$ tel que : $CA=4\;cm.$
2) Construire les axes de symétrique de $CARE.$
3) Calculer l'aire de $CARE.$
Exercice 7
1) Construire un losange $LOSA$ tel que : $LS=4\;cm\ $ et $\ AO=4\;cm.$
2) Construire en jaune les axes de symétrique de $LOSA.$
3) Calculer l'aire de $LOSA.$
Exercice 8
1) Construire un cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm$, $[AB]\ $ et $\ [CD]$ deux diamètres perpendiculaires.
2) Le cercle de centre $I$ de diamètre $[OA]$ coupe $(ID)$ en $J\ $ et $\ K$ ; $J$ es sur $[DI).$
3) Le cercle de centre $D$ passant par $I$ coupe $(\mathcal{C})$ en $F\ $ et $\ E.$
4) Le cercle de centre $D$ passant par $K$ coupe $(\mathcal{C})$ en $G\ $ et $\ H.$
5) Vérifier que $E\;,\ F\;,\ G\;,\ C\;,\ H$ sont les sommets d'un pentagone régulier.
Exercice 9
1) Construire un cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm.$
2) Marque les points $A$ et $B$ sur ce cercle tel que $mes\;\widehat{AOB}=\dfrac{360^{\circ}}{6}.$
3) Partage ce cercle en six parties égales.
4) Construire l'hexagone $ABCDEF.$
Exercice 10
1) Construis un trapèze rectangle $ABCD$ de bases $AB=5\;cm\;;\ CD=7\;cm$ et de hauteur $AD=3\;cm.$
2) Calcule son aire.
Exercice 11
1) Construis un trapèze isocèle $MNPQ$ si les bases $MN=4.5\;cm\;,\ PQ=8.5\;cm$ et de hauteur $4\;cm.$
2) Calcule son aire.
Exercice 12
1) Place trois points $A\;,\ B\ $ et $\ C$ non alignés.
2) Construis le point $D$ tel que $ABCD$ soit un parallélogramme.
3) Construis le point $E$ tel que $ADEC$ soit un parallélogramme.
Exercice 13
1) Construis un triangle $ABC$ isocèle en $C.$
2) Trace la droite parallèle à $(AC)$ passant par $B.$
3) Trace la droite parallèle à $(AB)$ passant par $C$, ces deux droites se coupent en $D.$
4) Donne la nature du quadrilatère $ABDC.$
Exercice 14
1) Soit un triangle $MNP$ rectangle en $M.$
La parallèle à $(MP)$ passant par $N$ coupe la parallèle à $(MN)$ passant par $P$ en $O.$
2) Quelle est la nature du quadrilatère $MNOP\ ?$
3) Construis le cercle $(C)$ de diamètre $[NP].$
4) Justifie que ce cercle passe par $M\ $ et $\ O.$
Exercice 15
1) Trace un segment $[EF]$ tel que : $EF=3\;cm$
2) Construis un carré et un triangle ayant pour coté commun $[EF].$
3) Quelle sera la hauteur de ce triangle si on veut que son aire soit égale à l'aire du carré ?
Exercice 16
1) Trace un segment $[AB]$ de $7\;cm.$ Construis le cercle $(C)$ de centre $A$ et de rayon $5\;cm$ et le cercle $(C')$ de centre $B$ et de rayon $5\;cm.$
Ces deux cercles se coupent en $E\ $ et $\ F.$
2) Donne la nature des triangles $ABE\ $ et $\ ABF.$
3) Que représente la droite $(AB)$ pour les deux triangles $ABE\ $ et $\ ABF.$
Exercice 17
Le périmètre d'un triangle est $21\;cm.$
Les deux cotés mesurent respectivement $6.5\;cm\ $ et $\ 8\;cm.$
1) Calcule la longueur du $3^{\text{ième}}$ côté.
2) Construis ce triangle.
3) Donne sa nature.
Exercice 18
Le centre du cercle tracé par Mamadou a été effacé.
Aide-le à retrouver le centre.

Exercice 19
1) Recopie et complète le tableau suivant :
$C$ est la longueur du coté du carré, son périmètre $P$ et son aire $A.$
$$\begin{array}{|c|c|c|c|c|}\hline C&3\;cm&7\;dm&&\\\hline P&&&32\;mm& \\\hline A&&&&36\;m^{2}\\\hline\end{array}$$
Exercice 20
Recopie et complète le tableau suivant. $P$ est le périmètre du rectangle et $A$ son aire.
$$\begin{array}{|c|c|c|c|c|}\hline\text{Longueur}&3.5\;dm&7.4\;cm&20\;cm&7.2\;m\\\hline\text{largeur}&2.8\;dm&21\;mm&&\\\hline P&&&&45\;m\\\hline A&&&360\;cm^{2}&\\\hline\end{array}$$
Exercice 21
Calcule l'aire d'un disque dans chacun des cas ci-dessous.
Tu donneras la valeur exacte, puis une valeur approchée au dixième.
a) Rayon : $4\;cm$
b) diamètre : $6\;m$
Exercice 22
1) Construis un rectangle $ABCD$ tel que : $AB=5\;cm\ $ et $\ BC=4\;cm$
2) Place les points $I$ et $J$ milieux respectifs des segments $[AB]\ $ et $\ [BC].$
3) Trace la parallèle à $(BC)$ passant par $I$ et qui coupe $[DC]$ en $K.$
4) Trace la parallèle à $(AB)$ passant par $J$ et qui coupe $[AD]$ en $H.$
5) Marque $L$ le point d'intersection de $(HJ)\ $ et $\ (IK).$
6) Calcule les aires des quadrilatères suivants : $DKLH\;,\ KCJL\ $ et $\ AILH.$
Exercice 23
La figure ci-dessous est un champ qui a la forme d'un trapèze rectangle dont les dimensions sont :
$$AD=80\;m\;;\ DH=150\;m\ \text{ et }\ DC=220\;m$$
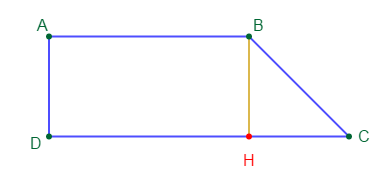
1) Calcule $HC$
2) Calcule l'aire du champ en $m^{2}$ puis en hectares
Exercice 24
Soit $ABCD$ un carré de $12\;cm$ de côté
Soient $E\;,\ F\;,\ $ et $\ H$ les milieux respectifs de $[AB]\;,\ [BC]\;,\ [CD]\ $ et $\ [DA]$
Calcule l'aire de $EFGH.$
Exercice 25
Le périmètre d'un jardin carré est $72\;m.$
Calcule son aire.
Exercice 26
Un terrain rectangulaire a pour périmètre $72\;m$ et sa longueur dépasse de $11\;m$ sa largeur.
Calcule son aire.
Exercice 27
On donne un rectangle de dimensions $5.1\;cm\ $ et $\ 3.3\;cm.$
a) Construis un carré ayant le même périmètre que ce rectangle.
b) Le rectangle et le carré ont-ils la même aire ?
justifie ta réponse.
Exercice 28
Une boite a la forme d'un pavé droit de largeur $15\;cm$, de longueur $20\;cm$ et de hauteur $8\;cm.$
Quelle surface de papier faut-il pour recouvrir cette boite ?
Exercice 29
Considère le polygone $ABCDE$ représenté ci-dessous :
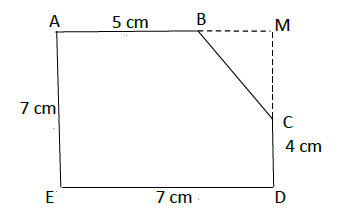
Les droites $(AB)\ $ et $\ (CD)$ se coupent en $M.$
Sachant que le quadrilatère $AMDE$ est un carré.
Propose une méthode pour trouver l'aire du polygone $ABCDE$
Exercice 30
Moussa souhaite entourer, avec du grillage, son jardin carré de $24\;m$ de côté, en laissant une ouverture de $4\;m$ de large.
Le grillage choisi coute $5\,000\;F$ le mètre.
Quel sera le prix à payer ?
Exercice 31
Un terrain communal est formé de deux parcelles juxtaposées: un carré de $1\;km$ de côté et un triangle rectangle dont les côtés de l'angle droit mesurent $0.6\;km\;,\ 0.8\;km$ et l'hypoténuse $1\;km.$
Le maire de cette commune veut procéder à un découpage de ce terrain en parcelles d'habitats de $15\;m$ sur $20\;m.$
Les $30\%$ du terrain sont réservés aux espaces publics.1)
Fais la figure (Échelle : $1\;cm$ représente $200\;m$).
Chaque parcelle est cédée à $1\,500\;F$ le $m^{2}\ $ et $\ 18\%$ de $TVA$ est appliquée au coût de la parcelle.
Ton grand-père veut acheter trois parcelles.
1) Aide le maire à déterminer le nombre de parcelles.
2) Calcule la somme que ton grand père doit verser
Auteur:
Diny Faye & adem

Ajouter un commentaire