Solution des exercices : Les angles - 6e
Classe:
Sixième
Exercice 1
On considère la figure ci-dessous.
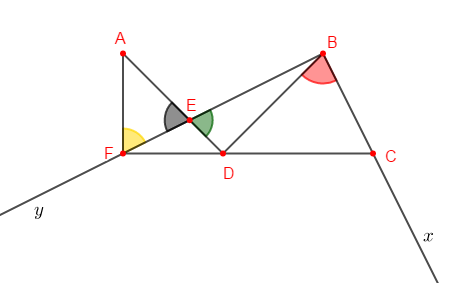
1) Colorions en rouge l'angle $\widehat{DBx}$
2) Colorions en vert l'angle $\widehat{DEB}$
3) Colorions en Jaune l'angle $\widehat{AFE}$
4) Colorions en noir l'angle $\widehat{AEF}$
Exercice 2
On considère la figure ci-dessous.

1) Donnons quatre autres façons de noter l'angle $\widehat{AOP}.$
$$\widehat{POA}\;,\ \widehat{MOB}\;,\ \widehat{AOB}\;,\ \widehat{MOP}$$
2) Colorions en vert l'angle $\widehat{ANM}.$
3) Donner cinq autres façons de noter l'angle $\widehat{ANM}.$
$$\widehat{MNA}\;,\ \widehat{ANB}\;,\ \widehat{PNM}\;,\ \widehat{PNB}\;,\ \widehat{BNP}$$
Exercice 3
1) Construisons un angle $\widehat{ABC}$ tel que : $mes\;\widehat{ABC}=50^{\circ}.$
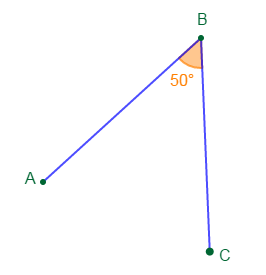
2) Donnons la nature de l'angle $\widehat{ABC}.$
On a : $mes\;\widehat{ABC}=50^{\circ}.$
Or, $50^{\circ}$ est inférieur à $90^{\circ}$
Donc, $\widehat{ABC}$ est un angle aigu.

Exercice 4 : "Construction et calcul d'angle"
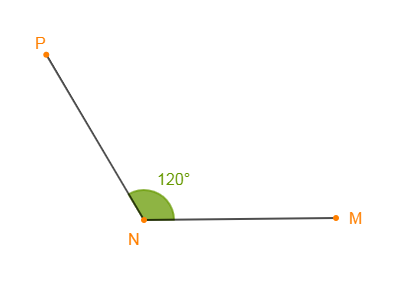
1) Construisons un angle $\widehat{MNP}$ tel que : $mes\;\widehat{MNP}=120^{\circ}.$
2) Donnons la nature de l'angle $\widehat{MNP}.$
On a : $mes\;\widehat{MNP}=120^{\circ}.$
Alors, $\widehat{MNP}$ est un angle dont la mesure est supérieure à $90^{\circ}.$
Donc, $\widehat{MNP}$ est un angle obtus.

Exercice 5 : "Angle droit et angle plat"
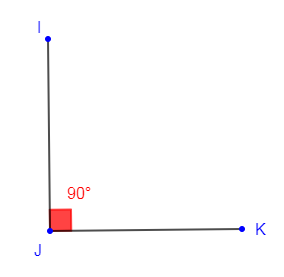
1) Construisons un angle droit $\widehat{IJK}.$
On construit donc un angle $\widehat{IJK}$ dont la mesure est égale à $90^{\circ}.$

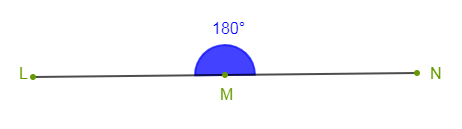
2) Construisons un angle plat $\widehat{LMN}.$
On construit alors un angle $\widehat{LMN}$ dont la mesure est égale à $180^{\circ}.$

Exercice 6
1) a) Traçons une demi-droite $[SU).$
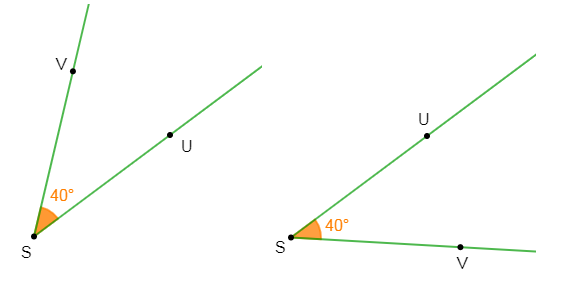
b) Construisons une demi-droite $[SV)$ telle que $mes\;\widehat{USV}=40^{\circ}.$
2) Il y a deux possibilités pour construire la demi-droite $[SV).$
La demi-droite $[SV)$ peut être placée au dessus ou en dessous de la demi-droite $[SU)$ telle que $mes\;\widehat{USV}=40^{\circ}.$
Donc, il y a deux possibilités.

Exercice 7
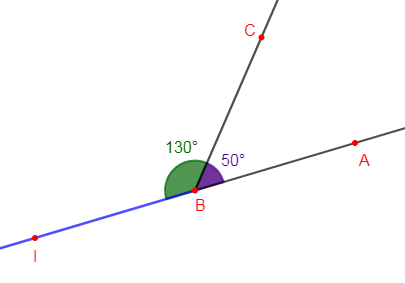
1) Traçons un angle $\widehat{ABC}$ de $50^{\circ}.$ Traçons une demi-droite $[BI)$ opposée à la demi-droite $[BA).$
2) Calculons $mes\;\widehat{CBI}$ en degré puis en grade.
Comme la demi-droite $[BI)$ est opposée à la demi-droite $[BA)$ alors, l'angle $\widehat{ABI}$ est un angle plat.
Donc, les angles $\widehat{ABC}\ $ et $\ \widehat{CBI}$ sont adjacents supplémentaires.
Ce qui signifie que la somme de leur mesure est égale à $180^{\circ}.$
Ainsi,
$$mes\;\widehat{ABC}+mes\;\widehat{CBI}=180^{\circ}$$
Ce qui entraine alors,
$$mes\;\widehat{CBI}=180^{\circ}-mes\;\widehat{ABC}$$
En remplaçant $mes\;\widehat{ABC}$ par sa valeur $50^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{CBI}&=&180^{\circ}-mes\;\widehat{ABC}\\\\&=&180^{\circ}-50^{\circ}\\\\&=&130^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{CBI}=130^{\circ}}$
Pour convertir en grades, on utilise la relation suivante : $90^{\circ}=100\;grades$
Ainsi, on a :
$130^{\circ}=\dfrac{100\times 130}{90}=144.44\;grades$
Donc, $\boxed{mes\;\widehat{CBI}=144.44\;gr}$

Exercice 8 : "Angle complémentaire"
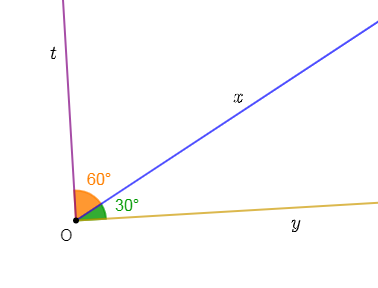
1) Construisons deux angles adjacents complémentaires $\widehat{xOy}\ $ et $\ \widehat{xOt}$ tels que : $mes\;\widehat{xOy}=30^{\circ}.$
2) Calculons $mes\;\widehat{xOt}$ en degré puis en grade.
Comme $\widehat{xOy}\ $ et $\ \widehat{xOt}$ sont deux angles adjacents complémentaires alors, cela signifie que la somme de leur mesure est égale à $90^{\circ}.$
Donc,
$$mes\;\widehat{xOy}+mes\;\widehat{xOt}=90^{\circ}$$
Ce qui entraine alors,
$$mes\;\widehat{xOt}=90^{\circ}-mes\;\widehat{xOy}$$
En remplaçant $mes\;\widehat{xOy}$ par sa valeur $30^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{xOt}&=&90^{\circ}-mes\;\widehat{xOy}\\\\&=&90^{\circ}-30^{\circ}\\\\&=&60^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{xOt}=60^{\circ}}$
Pour convertir en grades, on utilise la relation suivante : $90^{\circ}=100\;grades$
Donc, on a :
$60^{\circ}=\dfrac{100\times 60}{90}=66.66\;grades$
Ainsi, $\boxed{mes\;\widehat{xOt}=66.66\;gr}$

Exercice 9 : "Bissectrice d'un angle"
1) Construisons un angle $\widehat{ABC}$ tel que : $mes\;\widehat{ABC}=30^{\circ}.$
2) Construisons la demi-droite $[BJ)$ bissectrice de l'angle $\widehat{ABC}.$
Calculons $mes\;\widehat{JBA}.$
On sait que la bissectrice d'un angle partage l'angle en deux angles de même mesure.
Cela signifie que :
$$mes\;\widehat{JBA}=mes\;\widehat{JBC}=\dfrac{mes\;\widehat{ABC}}{2}$$
En remplaçant $mes\;\widehat{ABC}$ par sa valeur $30^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{JBA}&=&\dfrac{mes\;\widehat{ABC}}{2}\\\\&=&\dfrac{30^{\circ}}{2}\\\\&=&15^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{JBA}=15^{\circ}}$

Exercice 10 : "Symétrique d'un angle"
1) Deux angles superposables sont deux angles égaux.
2) Construisons deux angles adjacents et superposables dont chacun mesure $30^{\circ}.$
$\widehat{ABC}\ $ et $\ \widehat{CBD}$ sont deux angles adjacents et superposables de même mesure $30^{\circ}.$
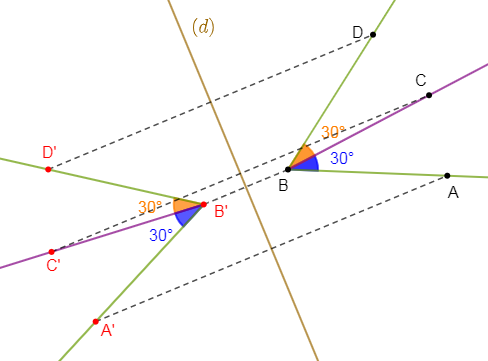
3) Construisons le symétrique de ces deux angles par rapport à une droite $(d).$
Alors, les angles $\widehat{A'B'C'}\ $ et $\ \widehat{C'B'D'}$ sont les symétriques respectifs des angles $\widehat{ABC}\ $ et $\ \widehat{CBD}$ par rapport à la droite $(d).$

Exercice 11 : "Angle supplémentaire"
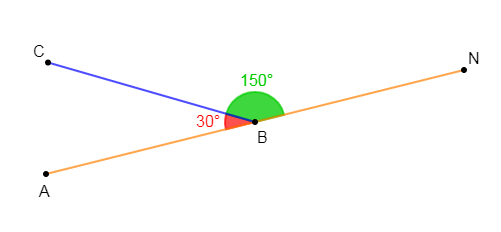
1) Construisons deux angles adjacents supplémentaires $\widehat{ABC}\ $ et $\ \widehat{CBN}$ tels que : $mes\;\widehat{ABC}=30^{\circ}.$
2) Calculons $mes\;\widehat{CBN}.$
Comme $\widehat{ABC}\ $ et $\ \widehat{CBN}$ sont deux angles adjacents supplémentaires alors, cela signifie que la somme de leur mesure est égale à $180^{\circ}.$
Donc,
$$mes\;\widehat{ABC}+mes\;\widehat{CBN}=180^{\circ}$$
Ce qui entraine alors,
$$mes\;\widehat{CBN}=180^{\circ}-mes\;\widehat{ABC}$$
En remplaçant $mes\;\widehat{ABC}$ par sa valeur $30^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{CBN}&=&180^{\circ}-mes\;\widehat{ABC}\\\\&=&180^{\circ}-30^{\circ}\\\\&=&150^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{CBN}=150^{\circ}}$

Exercice 12 : "Approfondissement"
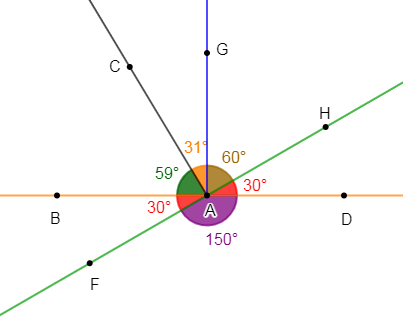
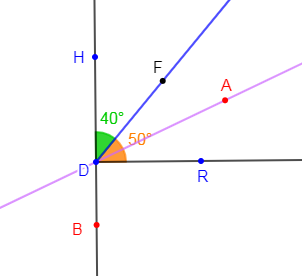
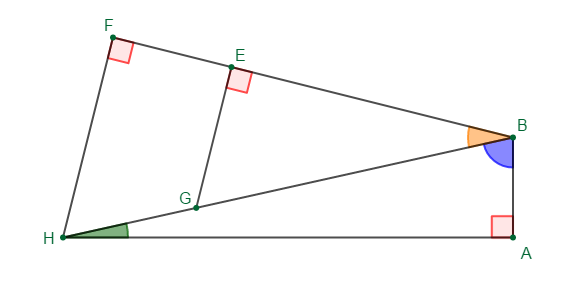
On considère la figure ci-dessous.
On donne $mes\;\widehat{CAB}=59^{\circ}\ $ et $\ mes\;\widehat{HAD}=30^{\circ}.$
1) Reproduisons la figure ci-dessous.

2) Calculons la mesure des angles : $mes\;\widehat{DAC}\;;\ mes\;\widehat{GAH}\;;\ mes\;\widehat{GAC}\;;\ mes\;\widehat{FAD}\ $ et $\ mes\;\widehat{FAB}$
$-\ $ Calcul de $mes\;\widehat{DAC}$
Les angles $\widehat{DAC}\ $ et $\ \widehat{CAB}$ sont adjacents supplémentaires donc, on a :
$$mes\;\widehat{DAC}+mes\;\widehat{CAB}=180^{\circ}$$
Ce qui entraine :
$$mes\;\widehat{DAC}=180^{\circ}-mes\;\widehat{CAB}$$
En remplaçant $mes\;\widehat{CAB}$ par sa valeur $59^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{DAC}&=&180^{\circ}-mes\;\widehat{CAB}\\\\&=&180^{\circ}-59^{\circ}\\\\&=&121^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{DAC}=121^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{GAH}$
Les angles $\widehat{GAH}\ $ et $\ \widehat{HAD}$ sont adjacents complémentaires. Ce qui signifie alors :
$$mes\;\widehat{GAH}+mes\;\widehat{HAD}=90^{\circ}$$
Ce qui entraine :
$$mes\;\widehat{GAH}=90^{\circ}-mes\;\widehat{HAD}$$
En remplaçant $mes\;\widehat{HAD}$ par sa valeur $30^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{GAH}&=&90^{\circ}-mes\;\widehat{HAD}\\\\&=&90^{\circ}-30^{\circ}\\\\&=&60^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{GAH}=60^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{GAC}$
Les angles $\widehat{GAC}\ $ et $\ \widehat{CAB}$ sont adjacents complémentaires donc, on a :
$$mes\;\widehat{GAC}+mes\;\widehat{CAB}=90^{\circ}$$
Ce qui entraine :
$$mes\;\widehat{GAC}=90^{\circ}-mes\;\widehat{CAB}$$
En remplaçant $mes\;\widehat{CAB}$ par sa valeur $59^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{GAC}&=&90^{\circ}-mes\;\widehat{CAB}\\\\&=&90^{\circ}-59^{\circ}\\\\&=&31^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{GAC}=31^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{FAD}$
Les angles $\widehat{FAD}\ $ et $\ \widehat{HAD}$ sont adjacents supplémentaires. Ce qui signifie alors :
$$mes\;\widehat{FAD}+mes\;\widehat{HAD}=180^{\circ}$$
Ce qui entraine :
$$mes\;\widehat{FAD}=180^{\circ}-mes\;\widehat{HAD}$$
En remplaçant $mes\;\widehat{HAD}$ par sa valeur $30^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{FAD}&=&180^{\circ}-mes\;\widehat{HAD}\\\\&=&180^{\circ}-30^{\circ}\\\\&=&150^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{FAD}=150^{\circ}}$
$-\ $ Calcul de $mes\;\widehat{FAB}$
On remarque que $\widehat{FAB}\ $ et $\ \widehat{HAD}$ sont deux angles superposables.
Ils ont alors la même mesure.
$$mes\;\widehat{FAB}=mes\;\widehat{HAD}$$
Or, $mes\;\widehat{HAD}=30^{\circ}$
D'où, $\boxed{mes\;\widehat{FAB}=30^{\circ}}$
Exercice 13 : "Approfondissement"
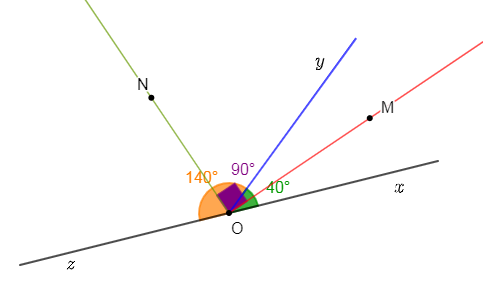
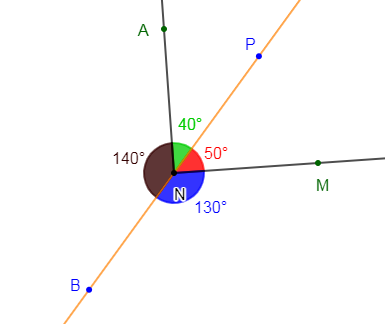
1) Construire deux angles adjacents $\widehat{xOy}\ $ et $\ \widehat{yOz}$ de côté commun $[Oy)$ tels que : $mes\;\widehat{xOy}=40^{\circ}\ $ et $\ mes\;\widehat{yOz}=140^{\circ}$
2) Calculons $mes\;\widehat{xOz}$ puis donnons sa nature.
Comme les deux angles $\widehat{xOy}\ $ et $\ \widehat{yOz}$ sont adjacents de côté commun $[Oy)$ alors, on a :
$$mes\;\widehat{xOy}+mes\;\widehat{yOz}=mes\;\widehat{xOz}$$
En remplaçant $mes\;\widehat{xOy}\ $ et $\ mes\;\widehat{yOz}$ par leur valeur, on obtient :
$\begin{array}{rcl} mes\;\widehat{xOz}&=&mes\;\widehat{xOy}+mes\;\widehat{yOz}\\\\&=&40^{\circ}+140^{\circ}\\\\&=&180^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{xOz}=180^{\circ}}$
La mesure de l'angle $\widehat{xOz}$ étant égale à $180^{\circ}$ alors, $\widehat{xOz}$ est un angle plat.
3) a) Construisons les demi-droites $[OM)\ $ et $\ [ON)$ bissectrices respectives des angles $\widehat{xOy}\ $ et $\ \widehat{yOz}$
b) Calculons $mes\;\widehat{MON}$ puis donnons sa nature.
On constate que les deux angles $\widehat{MOy}\ $ et $\ \widehat{yON}$ sont adjacents.
Donc, on a :
$$\widehat{MON}=\widehat{MOy}+\widehat{yON}$$
Comme $[OM)$ est bissectrice de l'angle $\widehat{xOy}$ alors, on a :
$$\widehat{xOM}=\widehat{MOy}=\dfrac{\widehat{xOy}}{2}$$
Ce qui donne : $\widehat{MOy}=\dfrac{40^{\circ}}{2}=20^{\circ}$
Comme $[ON)$ est bissectrice de l'angle $\widehat{yOz}$ alors, on a :
$$\widehat{yON}=\widehat{NOz}=\dfrac{\widehat{yOz}}{2}$$
Ce qui donne : $\widehat{yON}=\dfrac{140^{\circ}}{2}=70^{\circ}$
Ainsi, en remplaçant $\widehat{MOy}\ $ et $\ \widehat{yON}$ par leur valeur, on obtient :
$\begin{array}{rcl} mes\;\widehat{MON}&=&\widehat{MOy}+\widehat{yON}\\\\&=&20^{\circ}+70^{\circ}\\\\&=&90^{\circ}\end{array}$
D'où, $\boxed{mes\;\widehat{MON}=90^{\circ}}$
L'angle $\widehat{MON}$ a donc pour mesure $90^{\circ}.$
C'est alors un angle droit.

Exercice 14 : "Approfondissement"
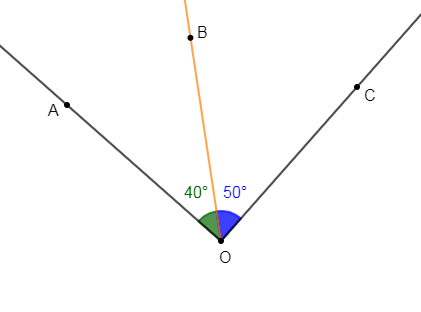
1) a) Construisons deux angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ de côté commun $[OB)$ tels que : $mes\;\widehat{AOB}=40^{\circ}\ $ et $\ mes\;\widehat{BOC}=50^{\circ}$
b) Les angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ sont adjacents complémentaires.
Justifions la réponse.
On constate que les deux angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ ont un sommet commun ; le point $O$ et sont situés de part et d'autre d'un bord commun ; le côté $[OB).$
Donc, ces deux angles sont adjacents.
De plus, on a :
$mes\;\widehat{AOB}+mes\;\widehat{BOC}=40^{\circ}+50^{\circ}=90^{\circ}$
Comme la somme de leur mesure est égale à $90^{\circ}$ alors, ces deux angles sont complémentaires.
D'où, les angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ sont adjacents complémentaires.
c) Calculons la mesure de l'angle $\widehat{AOC}$ en degré $(^{\circ})$ puis en grade $(gr).$
Comme les angles $\widehat{AOB}\ $ et $\ \widehat{BOC}$ sont adjacents complémentaires alors, on a :
$$mes\;\widehat{AOB}+mes\;\widehat{BOC}=mes\;\widehat{AOC}$$
D'où, $\boxed{mes\;\widehat{AOC}=90^{\circ}}$
On sait que : $90^{\circ}=100\;grades$
Donc, la mesure de l'angle $\widehat{AOC}$ en grade $(gr)$ est égale à $100\;gr.$

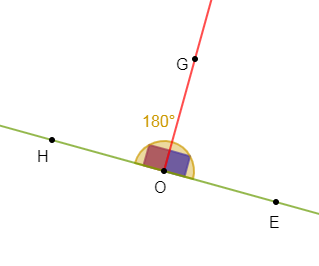
2) a) Construisons un angle droit $\widehat{EOG}$ puis marquons le point $H$ tel que $\widehat{EOH}$ soit un angle plat.
b) Les angles $\widehat{EOG}\ $ et $\ \widehat{GOH}$ sont adjacents supplémentaires et de même mesure $90^{\circ}$
c) La droite $(GO)$ est la bissectrice de l'angle $\widehat{EOH}.$
On remarque que la droite $(GO)$ passant par le sommet $O$, partage l'angle $\widehat{EOH}$ en deux angles de même mesure $90^{\circ}.$
Par conséquent, la droite $(GO)$ représente la bissectrice de l'angle $\widehat{EOH}.$
Calculons $mes\;\widehat{EOH}.$
On sait que $\widehat{EOH}$ est un angle plat. Ce qui signifie que sa mesure est égale à $180^{\circ}.$
Ainsi, $\boxed{mes\;\widehat{EOH}=180^{\circ}}$

Exercice 15
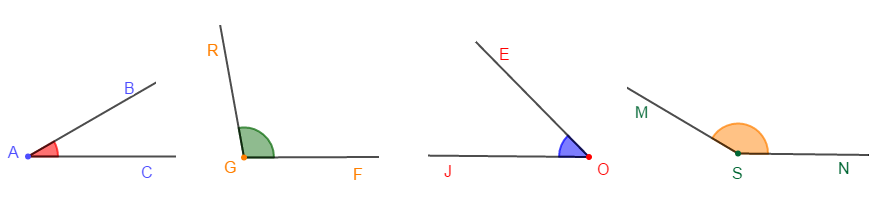
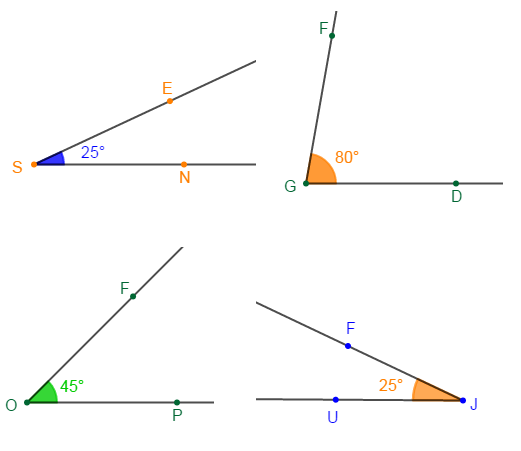
On donne les angles de la figure ci-dessous :

1) Nommons chacun des angles de la figure.
$\widehat{CAB}\;,\ \widehat{FGR}\;,\ \widehat{EOJ}\;,\ \widehat{NSM}$
2) Pour chaque angle précisons son sommet et ses côtés.
L'angle $\widehat{CAB}$ a pour sommet $A$ et pour côtés $[AB)\ $ et $\ [AC)$
L'angle $\widehat{FGR}$ a pour sommet $G$ et pour côtés $[GR)\ $ et $\ [GF)$
L'angle $\widehat{EOJ}$ a pour sommet $O$ et pour côtés $[OJ)\ $ et $\ [OE)$
L'angle $\widehat{NSM}$ a pour sommet $S$ et pour côtés $[SM)\ $ et $\ [SN)$
3) Mesurons chaque angle puis donnons la mesure en grade.
En mesurant chaque angle, on trouve :
$\widehat{CAB}=30^{\circ}$
$\widehat{FGR}=100^{\circ}$
$\widehat{EOJ}=45^{\circ}$
$\widehat{NSM}=150^{\circ}$
Pour convertir en grades, on utilise la relation suivante : $90^{\circ}=100\,grades$
Ainsi,
$30^{\circ}=\dfrac{100\times 30}{90}=33\,grades$
$100^{\circ}=\dfrac{100\times 100}{90}=111\,grades$
$45^{\circ}=\dfrac{100\times 45}{90}=50\,grades$
$150^{\circ}=\dfrac{100\times 150}{90}=166\,grades$
Donc,
$\widehat{CAB}=33\,grades$
$\widehat{FGR}=111\,grades$
$\widehat{EOJ}=50\,grades$
$\widehat{NSM}=166\,grades$
4) Indiquons parmi ces angles ceux qui sont aigus, plats, obtus ou droits.
Les angles $\widehat{CAB}\ $ et $\ \widehat{EOJ}$ ont une mesure inférieure à $90^{\circ}$
Donc, ces angles sont des angles aigus.
Par contre, les angles $\widehat{FGR}\ $ et $\ \widehat{NSM}$ ont une mesure supérieure à $90^{\circ}$ et inférieure à $180^{\circ}.$
Par conséquent, ces angles sont des angles obtus.
Exercice 16
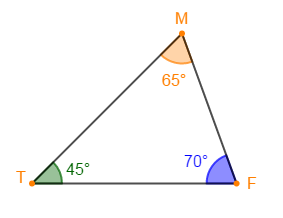
$TMF$ est un triangle tel que $\widehat{TMF}=65^{\circ}.$

1) En mesurant les angles $\widehat{MTF}\ $ et $\widehat{TFM}$, on trouve :
$$\widehat{MTF}=45^{\circ}\ \text{ et }\ \widehat{TFM}=70^{\circ}$$
2) Calculons la somme des trois angles du triangle.
Soit : $\widehat{TMF}+\widehat{MTF}+\widehat{TFM}=65^{\circ}+45^{\circ}+70^{\circ}=180^{\circ}$
Exercice 17


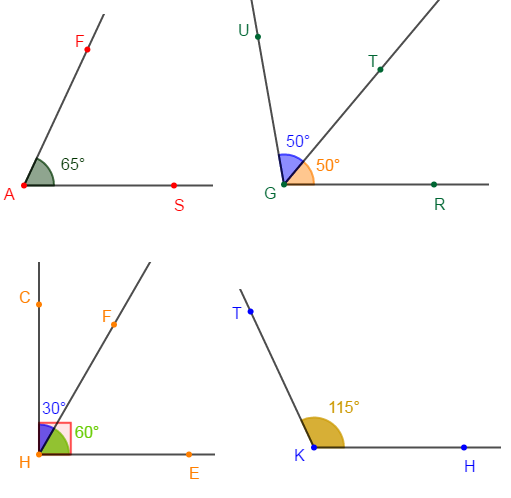
1) Complétons les phrases par les mots ou groupe de mots ci-dessous et justifions notre réponse.
complémentaires ; supplémentaires ; correspondants ; bissectrice ; superposables ; adjacents ; angle droit ; angle obtus ; angle aigu ; angle plat.
a) Les angles $\widehat{CHF}\ $ et $\ \widehat{FHE}$ sont adjacents complémentaires.
On a : $\widehat{CHF}+\widehat{FHE}=30^{\circ}+60^{\circ}=90^{\circ}$ donc, ces deux angles sont complémentaires.
De plus, $\widehat{CHF}\ $ et $\ \widehat{FHE}$ ont le même sommet $H$ et sont situés de part et d'autre du côté commun $[HF)$ donc, ils sont adjacents.
Par conséquent, les angles $\widehat{CHF}\ $ et $\ \widehat{FHE}$ sont adjacents complémentaires.
b) Les angles $\widehat{SAF}\ $ et $\ \widehat{TKH}$ sont supplémentaires
On a : $\widehat{SAF}+\widehat{TKH}=65^{\circ}+115^{\circ}=180^{\circ}$
Donc, $\widehat{SAF}\ $ et $\ \widehat{TKH}$ sont supplémentaires.
c) Les angles $\widehat{SAF}\ $ et $\ \widehat{FJU}$ sont complémentaires
On a : $\widehat{SAF}+\widehat{FJU}=65^{\circ}+25^{\circ}=90^{\circ}$
Ce qui montre que les angles $\widehat{SAF}\ $ et $\ \widehat{FJU}$ sont complémentaires.
d) Les angles $\widehat{ESN}\ $ et $\ \widehat{FJU}$ sont correspondants
e) $\widehat{TKH}$ est un angle obtus
La mesure de l'angle $\widehat{TKH}$ est supérieure à $90^{\circ}$ mais inférieure à $180^{\circ}.$
Donc, l'angle $\widehat{TKH}$ est un angle obtus.
f) $\widehat{FOP}$ est un angle aigu
Comme la mesure de l'angle $\widehat{FOP}$ est inférieure à $90^{\circ}$ alors, $\widehat{FOP}$ est un angle aigu.
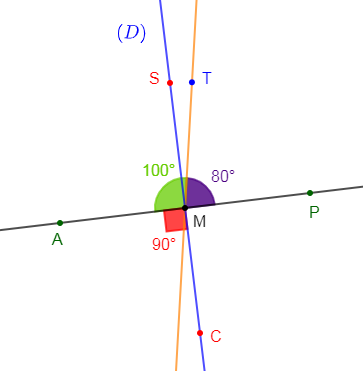
g) Les angles $\widehat{UGR}\ $ et $\ \widehat{FGD}$ sont supplémentaires
On a : $\widehat{UGR}+\widehat{FGD}=100^{\circ}+80^{\circ}=180^{\circ}.$
Ce qui prouve que les angles $\widehat{UGR}\ $ et $\ \widehat{FGD}$ sont supplémentaires
h) Les angles $\widehat{UGT}\ $ et $\ \widehat{TGR}$ sont adjacents et superposables
Les angles $\widehat{UGT}\ $ et $\ \widehat{TGR}$ ont le même sommet $G$, la même mesure $50^{\circ}$ et sont situés de part et d'autre du côté commun $[GT)$ donc, ils sont adjacents et superposables.
2) Répondons par vrai ou faux aux affirmations ci-dessous :
a) $[FH)$ est la bissectrice de l'angle $\widehat{CHE}.\quad\text{Faux}$
b) $[TG)$ est la bissectrice de l'angle $\widehat{UGR}.\quad\text{Vrai}$
c) Les angles $\widehat{FJU}\ $ et $\ \widehat{FOP}$ sont superposables.$\quad\text{Faux}$
d) Les angles $\widehat{TKH}\ $ et $\ \widehat{FGD}$ sont supplémentaires.$\quad\text{Faux}$
Exercice 18
Les questions sont indépendantes.
1) Construisons les angles suivants.
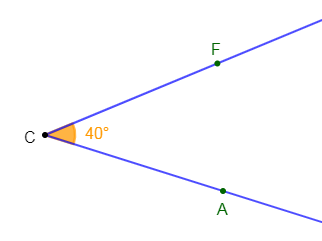
a) $\widehat{ACF}$ est un angle tel que $\widehat{ACF}=40^{\circ}.$

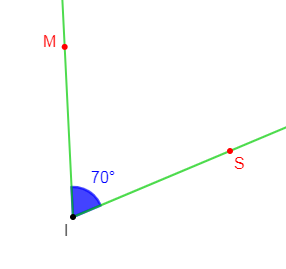
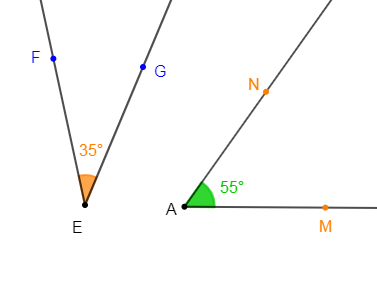
b) $\widehat{STM}$ est un angle tel que $\widehat{STM}=70^{\circ}.$

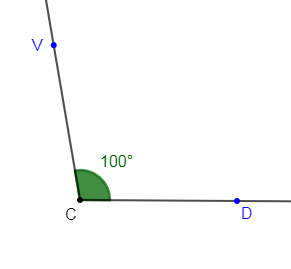
c) $\widehat{DCV}$ est un angle tel que $\widehat{DCV}=100^{\circ}.$

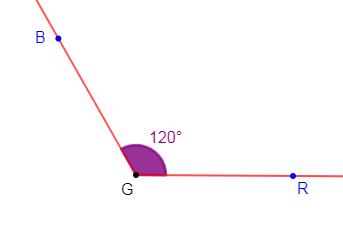
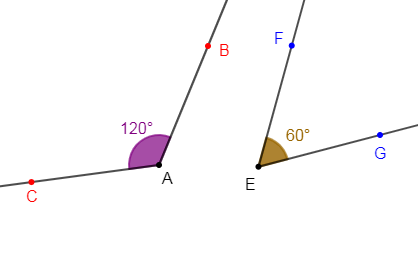
d) $\widehat{RGB}$ est un angle tel que $\widehat{RGB}=120^{\circ}.$

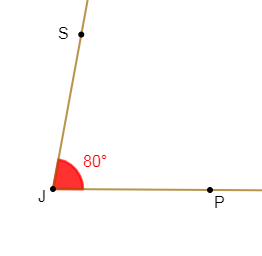
e) $\widehat{PJS}$ est un angle tel que $\widehat{PJS}=80^{\circ}.$

2) Construisons un angle $\widehat{MAN}$ tel que $\widehat{MAN}=55^{\circ}.$
Construisons l'angle $\widehat{GEF}$ pour que les angles $\widehat{MAN}\ $ et $\ \widehat{GEF}$ soient complémentaires.
Pour cela, on détermine la mesure de l'angle $\widehat{GEF}.$
Les angles $\widehat{MAN}\ $ et $\ \widehat{GEF}$ sont complémentaires donc, on a :
$$mes\;\widehat{MAN}+mes\;\widehat{GEF}=90^{\circ}$$
Ce qui entraine : $mes\;\widehat{GEF}=90^{\circ}-mes\;\widehat{MAN}$
En remplaçant $mes\;\widehat{MAN}$ par sa valeur $55^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{GEF}&=&90^{\circ}-mes\;\widehat{MAN}\\\\&=&90^{\circ}-55^{\circ}\\\\&=&35^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{GEF}$ est égale à $35^{\circ}.$

3) Construisons un angle $\widehat{BAC}$ tel que $\widehat{BAC}=120^{\circ}.$
Construisons l'angle $\widehat{GEF}$ pour que les angles $\widehat{FEG}\ $ et $\ \widehat{BAC}$ soient supplémentaires.
Déterminons la mesure de l'angle $\widehat{GEF}.$
Les angles $\widehat{FEG}\ $ et $\ \widehat{GEF}$ sont supplémentaires donc, on a :
$$mes\;\widehat{FEG}+mes\;\widehat{GEF}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{GEF}=180^{\circ}-mes\;\widehat{FEG}$
En remplaçant $mes\;\widehat{FEG}$ par sa valeur $120^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{GEF}&=&180^{\circ}-mes\;\widehat{FEG}\\\\&=&180^{\circ}-120^{\circ}\\\\&=&60^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{GEF}$ est égale à $60^{\circ}.$

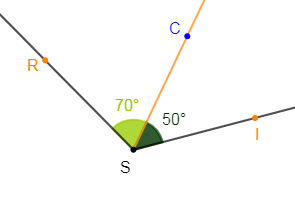
4) Construisons deux angles adjacents $\widehat{TSC}\ $ et $\ \widehat{CSR}$ tels que $\widehat{TSC}=50^{\circ}\ $ et $\ \widehat{CSR}=70^{\circ}.$
Les deux angles $\widehat{TSC}\ $ et $\ \widehat{CSR}$ ont alors un sommet commun ; le point $S$ et sont situés de part et d'autre d'un bord commun ; le côté $[SCF).$

Exercice 19
1) Construis deux angles adjacents $\widehat{MNP}\ $ et $\ \widehat{PNA}$ tels que $\widehat{MNP}=50^{\circ}\ $ et $\ \widehat{PNA}=40^{\circ}.$
2) Justifions que les angles $\widehat{MNP}\ $ et $\ \widehat{PNA}$ sont complémentaires.
Alors, on vérifie si la somme de leur mesure est égale à $90^{\circ}.$
On a : $mes\;\widehat{MNP}=50^{\circ}+mes\;\widehat{PNA}=50^{\circ}+40^{\circ}=90^{\circ}$
Ce qui justifie que les angles $\widehat{MNP}\ $ et $\ \widehat{PNA}$ sont complémentaires.
3) Plaçons le point $B$ sur la demi-droite $[PN)$ tel que le point $N$ soit le milieu de $[PB].$
4) Déterminons la mesure des angles $\widehat{MNB}\ $ et $\ \widehat{ANB}$ sachant que $\widehat{PNB}$ est un angle plat.
$-\ $ Calcul de $mes\;\widehat{MNB}$
Comme $\widehat{PNB}$ est un angle plat alors, sa mesure est égale à $180^{\circ}.$
Donc, les angles $\widehat{PNM}\ $ et $\ \widehat{MNB}$ sont adjacents supplémentaires.
Ce qui s'écrit alors :
$$mes\;\widehat{PNM}+mes\;\widehat{MNB}=mes\;\widehat{PNB}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{MNB}=180^{\circ}-mes\;\widehat{PNM}$
En remplaçant $mes\;\widehat{PNM}$ par sa valeur $50^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{MNB}&=&180^{\circ}-mes\;\widehat{PNM}\\\\&=&180^{\circ}-50^{\circ}\\\\&=&130^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{MNB}$ est égale à $130^{\circ}.$
$-\ $ Calcul de $mes\;\widehat{ANB}$
$\widehat{PNB}$ est un angle plat donc, sa mesure est égale à $180^{\circ}.$
Alors, les angles $\widehat{PNA}\ $ et $\ \widehat{ANB}$ sont adjacents supplémentaires.
Ainsi :
$$mes\;\widehat{PNA}+mes\;\widehat{ANB}=mes\;\widehat{PNB}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{ANB}=180^{\circ}-mes\;\widehat{PNA}$
On remplace $mes\;\widehat{PNA}$ par sa valeur $40^{\circ}.$
On obtient alors :
$\begin{array}{rcl} mes\;\widehat{ANB}&=&180^{\circ}-mes\;\widehat{PNA}\\\\&=&180^{\circ}-40^{\circ}\\\\&=&140^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{ANB}$ est égale à $140^{\circ}.$

Exercice 20
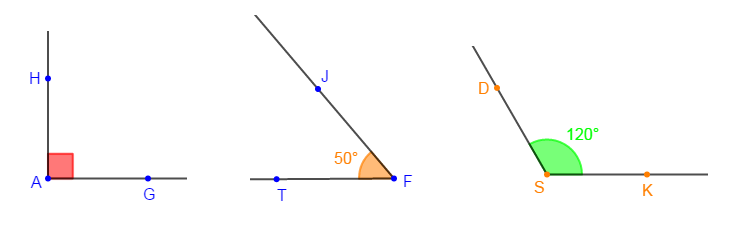
1) Reproduisons les angles de la figure en utilisant uniquement la règle et le compas.

2) Convertissons la mesure de chaque angle de la figure en grade.
On sait que : $90^{\circ}=100\;grades$
Donc, la mesure de l'angle droit $\widehat{GAH}$ est égale à $100\;gr.$
Comme $90^{\circ}$ correspond à $100\;grades$ alors :
$50^{\circ}$ correspond à $\dfrac{100\times 50}{90}=55.55\;grades$
$120^{\circ}$ correspond à $\dfrac{100\times 120}{90}=133.33\;grades$
Donc, la mesure de l'angle $\widehat{JFT}$ est égale à $55.55\;gr$ et celle de $\widehat{DSK}$ est égale à $133.33\;gr$
Exercice 21
Construisons la bissectrice de chacun des angles ci-dessous avec la règle et le rapporteur :
On sait que : la bissectrice d'un angle est la demi-droite ou la droite qui passe par le sommet de cet angle et qui le partage en deux angles de même mesure.
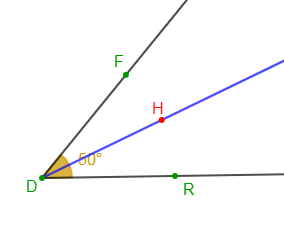
1) $\widehat{RDF}$ est un angle tel que mes $\widehat{RDF}=50^{\circ}$
On place le centre du rapporteur au sommet $D$ et le bord droit sur le côté $[DR)$ de l'angle $\widehat{RDF}.$
Puis, à la graduation $25^{\circ}$ correspondant à la moitié de la mesure de l'angle $\widehat{RDF}$, on marque le point $H.$
Ensuite, avec la règle, on trace la demi-droite $[DH)$ qui représente la bissectrice de l'angle $\widehat{RDF}.$

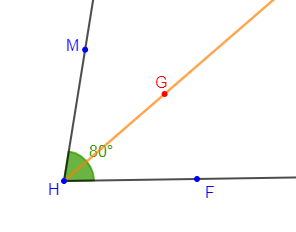
2) $\widehat{FHM}$ est un angle tel que mes $\widehat{FHM}=80^{\circ}$
On place le centre du rapporteur au sommet $H$ et le bord droit sur le côté $[HF)$ de l'angle $\widehat{FHM}.$
Puis, à la graduation $40^{\circ}$ correspondant à la moitié de la mesure de l'angle $\widehat{FHM}$, on marque le point $G.$
Ensuite, avec la règle, on trace la demi-droite $[HG)$ ; bissectrice de l'angle $\widehat{FHM}.$

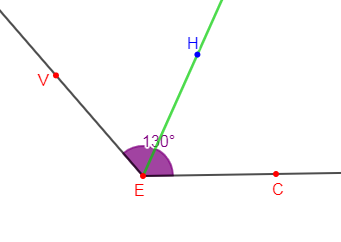
3) $\widehat{CEV}$ est un angle tel que mes $\widehat{CEV}=130^{\circ}$
En procédant de la même manière que dans les questions $1)$ et $2)$ on trace la demi-droite $[EH)$ ; bissectrice de l'angle $\widehat{CEV}.$

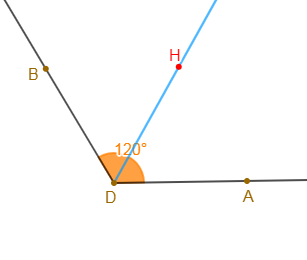
4) $\widehat{ADB}$ est un angle tel que mes $\widehat{ADB}=120^{\circ}$
On procède comme dans les questions précédentes pour tracer la bissectrice de l'angle $\widehat{ADB}$ représentée par la demi-droite $[DH).$

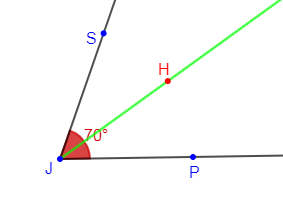
5) $\widehat{PJS}$ est un angle tel que mes $\widehat{PJS}=70^{\circ}$
De la même manière que dans les questions précédentes, on trace la demi-droite $[JH)$ qui est la bissectrice de l'angle $\widehat{PJS}.$

Exercice 22
Construisons la bissectrice de chacun des angles ci-dessous avec la règle et le compas :
Il faut se rappeler que : la bissectrice d'un angle est la demi-droite ou la droite qui passe par le sommet de cet angle et qui le partage en deux angles de même mesure.
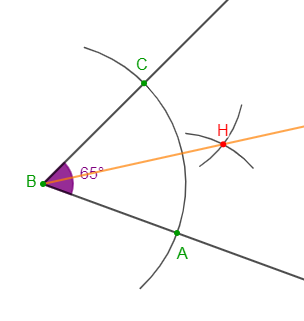
1) $\widehat{ABC}$ est un angle qui a pour mesure $65^{\circ}$
On pointe le compas sur le sommet $B$ et on trace un arc de cercle qui coupe les deux côtés de l'angle $\widehat{ABC}$ respectivement en $A\ $ et $\ C.$
Puis, on place sur $A$ et on trace un arc de cercle. Avec le même écartement du compas, on se place sur $C$ et on trace un arc de cercle. Les deux arcs de cercle se coupent au point $H.$
On trace ensuite, la demi-droite $[BH)$ qui est la bissectrice de l'angle $\widehat{ABC}.$

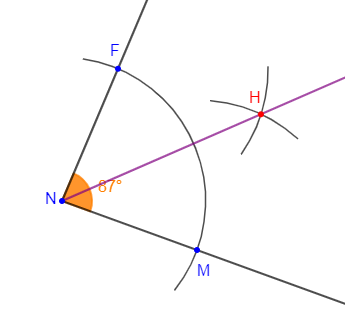
2) $\widehat{MNF}$ est un angle qui a pour mesure $87^{\circ}$
En procédant de la même manière que dans la question $1)$, on trace la demi-droite $[NH)$ ; bissectrice de l'angle $\widehat{MNF}.$

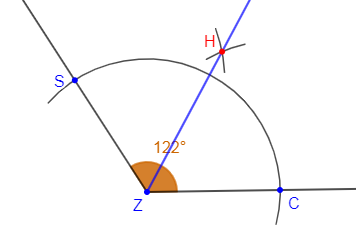
3) $\widehat{CZS}$ est un angle qui a pour mesure $122^{\circ}$
Avec la même démarche que dans la question $1)$, on trace la demi-droite $[ZH)$ qui représente la bissectrice de l'angle $\widehat{CZS}.$

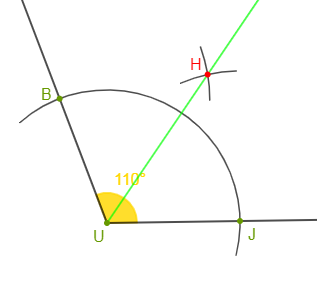
4) $\widehat{JUB}$ est un angle qui a pour mesure $110^{\circ}$
De la même manière que dans la question $1)$, on trace la demi-droite $[UH)$ ; bissectrice de l'angle $\widehat{JUB}.$

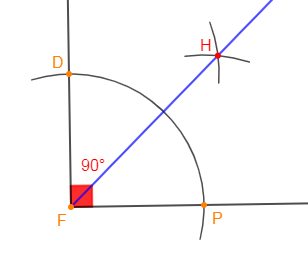
5) $\widehat{PFD}$ est un angle qui a pour mesure $90^{\circ}$
En procédant de la même manière que dans la question $1)$, on trace la demi-droite $[FH)$ qui est la bissectrice de l'angle $\widehat{PFD}.$

Exercice 23
1) Construisons deux angles complémentaires $\widehat{RDF}\ $ et $\ \widehat{FDH}$ tels que $\widehat{RDF}=50^{\circ}.$
2) Les angles $\widehat{RDF}\ $ et $\ \widehat{FDH}$ sont adjacents.
Justifions notre réponse.
En observant la figure, on constate que $\widehat{RDF}\ $ et $\ \widehat{FDH}$ sont deux angles qui ont un sommet commun ; le point $D$ et sont situés de part et d'autre d'un bord commun ; le coté $[DF).$
Par conséquent, ces deux angles sont adjacents.
3) Construisons la bissectrice $[DA)$ de l'angle $\widehat{RDF}.$
Cette bissectrice partage alors l'angle $\widehat{RDF}$ en deux angles de même mesure :
$$mes\;\widehat{RDA}=mes\;\widehat{ADF}=\dfrac{50^{\circ}}{2}=25^{\circ}$$
4) Plaçons le point $B$ sur la demi-droite $[HD)$ tel que $HB>DH.$
Déterminons la mesure de l'angle $\widehat{BDA}$ sachant que $\widehat{BDH}$ est un angle plat.
Comme $\widehat{BDH}$ est un angle plat alors, sa mesure est égale à $180^{\circ}.$
Donc, les angles $\widehat{BDA}\ $ et $\ \widehat{ADH}$ sont adjacents supplémentaires.
Ainsi, on a :
$$mes\;\widehat{BDA}+mes\;\widehat{ADH}=mes\;\widehat{BDH}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{BDA}=180^{\circ}-mes\;\widehat{ADH}$
On peut remarquer que les angles $\widehat{ADF}\ $ et $\ \widehat{FDH}$ sont adjacents.
Donc, $mes\;\widehat{ADH}=mes\;\widehat{ADF}+mes\;\widehat{FDH}$
On remplace alors $mes\;\widehat{ADH}$ par la somme : $mes\;\widehat{ADF}+mes\;\widehat{FDH}.$
On obtient alors :
$\begin{array}{rcl} mes\;\widehat{BDA}&=&180^{\circ}-mes\;\widehat{ADH}\\\\&=&180^{\circ}-\left(mes\;\widehat{ADF}+mes\;\widehat{FDH}\right)\\\\&=&180^{\circ}-(25^{\circ}+40^{\circ})\\\\&=&180^{\circ}-65^{\circ}\\\\&=&115^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{BDA}$ est égale à $115^{\circ}.$

Exercice 24
1) Construisons deux angles supplémentaires $\widehat{TMP}\ $ et $\ \widehat{TMA}$ tel que $\widehat{TMP}=80^{\circ}.$
2) Les angles $\widehat{TMP}\ $ et $\ \widehat{TMA}$ sont adjacents.
Justifions notre réponse.
En observant la figure, on remarque que $\widehat{TMP}\ $ et $\ \widehat{TMA}$ sont deux angles qui ont un sommet commun ; le point $M$ et sont situés de part et d'autre d'un bord commun ; le coté $[MT).$
Par conséquent, ces deux angles sont adjacents.
3) Traçons la droite $(D)$ perpendiculaire à $(AP)$ et passant par le point $M.$
Plaçons les points $C\ $ et $\ S$ sur $(D)$ tels que $M$ soit le milieu de $[CS].$
4) Déterminons la mesure de l'angle $\widehat{TMA}.$
Comme les angles $\widehat{TMP}\ $ et $\ \widehat{TMA}$ supplémentaires alors, on a :
$$mes\;\widehat{TMA}+mes\;\widehat{TMP}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{TMA}=180^{\circ}-mes\;\widehat{TMP}$
En remplaçant $mes\;\widehat{TMP}$ par sa valeur $80^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{TMA}&=&180^{\circ}-mes\;\widehat{TMP}\\\\&=&180^{\circ}-80^{\circ}\\\\&=&100^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{TMA}$ est égale à $100^{\circ}.$

Exercice 25

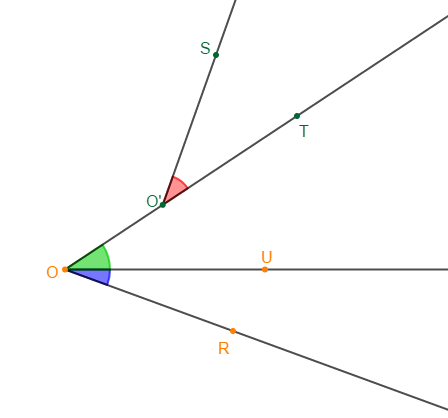
1) Les angles $\widehat{SO'T}\ $ et $\ \widehat{TOU}$ ne sont pas adjacents
Justifions notre réponse.
En observant la figure on constate que les angles $\widehat{SO'T}\ $ et $\ \widehat{TOU}$ n'ont pas le même sommet.
Par conséquent, ils ne sont pas adjacents.
2) Les angles $\widehat{TOU}\ $ et $\ \widehat{UOR}$ sont adjacents
Justifions notre réponse.
En observant la figure on remarque que $\widehat{TOU}\ $ et $\ \widehat{UOR}$ sont deux angles qui ont un sommet commun ; le point $O$ et sont situés de part et d'autre d'un bord commun ; le côté $[OU).$
Donc, ces deux angles sont adjacents.
3) Les angles $\widehat{SO'T}\ $ et $\ \widehat{UOR}$ ne sont pas adjacents.
Justifions notre réponse.
En observant la figure on constate que les angles $\widehat{SO'T}\ $ et $\ \widehat{UOR}$ n'ont ni de sommet commun, ni de côté commun.
Par conséquent, ils ne sont pas adjacents.
Exercice 26

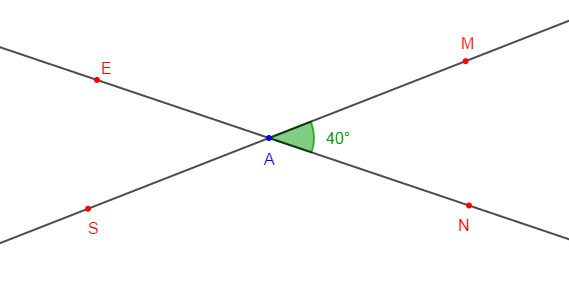
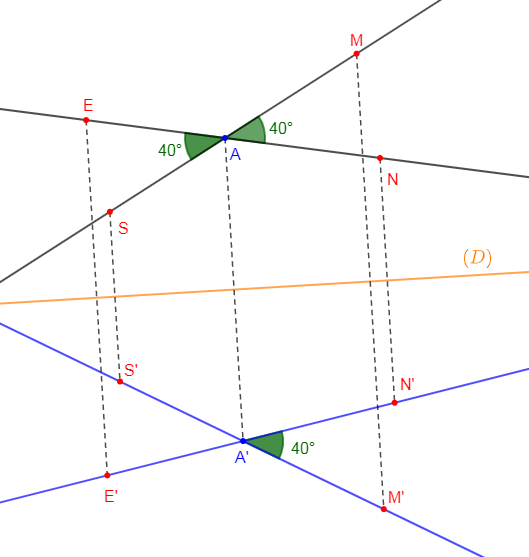
Sur la figure l'angle $\widehat{NAM}$ mesure $40^{\circ}\ $ et $\ (D)$ une droite du plan.
1) Les angles $\widehat{MAN}\ $ et $\ \widehat{EAS}$ sont superposables.
Déduisons-en la mesure de l'angle $\widehat{EAS}.$
On sait que deux angles superposables sont égaux.
Donc, la mesure de l'angle $\widehat{EAS}$ est égale à celle de l'angle $\widehat{MAN}.$
D'où, $\boxed{mes\;\widehat{EAS}=40^{\circ}}$
2) Reproduisons la figure en vrai grandeur en respectant l'angle $40^{\circ}.$
3) Construisons le symétrique de la figure par rapport à la droite $(D)$ ; les points points $A\;,\ M\;,\ N\;,\ E\ $ et $\ S$ ont symétriques respectifs $A'\;,\ M'\;,\ N'\;,\ E'\ $ et $\ S'$
4) Comparons les angles $\widehat{M'A'N'}\ $ et $\ \widehat{MAN}.$
On a : l'angle $\widehat{M'A'N'}$ est le symétrique de l'angle $\widehat{MAN}$ par rapport à la droite $(D).$
Or, on sait que : le symétrique d'un angle par rapport à un droite donnée est un angle de même mesure.
Par conséquent, les angles $\widehat{M'A'N'}\ $ et $\ \widehat{MAN}$ ont la même mesure.
D'où, $\boxed{mes\;\widehat{M'A'N'}=mes\;\widehat{MAN}=40^{\circ}}$

Exercice 27
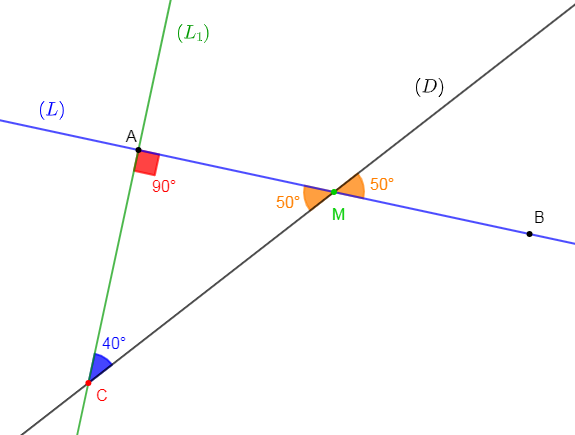
1) Traçons deux droites $(L)\ $ et $\ (D)$ sécantes au point $M$ formant un angle de $50^{\circ}.$
2) Plaçons les points $A\ $ et $\ B$ sur la droite $(L)$ tels que $AB=8\;cm\ $ et $\ M$ soit le milieu de $[AB].$
3) Traçons la droite $(L_{1})$ perpendiculaire à $(L)$ passant par le point $A$ ; elle coupe la droite $(D)$ au point $C.$
4) Déterminons la mesure de chacun des angles du triangle $AMC.$
Comme la droite $(L_{1})$ est perpendiculaire à la droite $(L)$ au point $A$ alors, $\widehat{MAC}$ est un angle droit.
D'où, $\boxed{mes\;\widehat{MAC}=90^{\circ}}$
En observant la figure, on constate que l'angle $\widehat{AMC}$ et l'angle de $50^{\circ}$ formé par les deux droites $(L)\ $ et $\ (D)$ sont superposables.
Par conséquent, ils ont la même mesure.
D'où, $\boxed{mes\;\widehat{AMC}=50^{\circ}}$
Comme $\widehat{MAC}$ est un angle droit alors, le triangle $AMC$ est rectangle en $A.$
Or, on sait que dans un triangle rectangle, les angles aigus sont complémentaires.
Ce qui signifie que : $\widehat{AMC}\ $ et $\ \widehat{ACM}$ sont complémentaires.
Ainsi :
$$mes\;\widehat{ACM}+mes\;\widehat{AMC}=90^{\circ}$$
Ce qui entraine : $mes\;\widehat{ACM}=90^{\circ}-mes\;\widehat{AMC}$
En remplaçant $mes\;\widehat{AMC}$ par sa valeur $50^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{ACM}&=&90^{\circ}-mes\;\widehat{AMC}\\\\&=&90^{\circ}-50^{\circ}\\\\&=&40^{\circ}\end{array}$
Donc, $\boxed{mes\;\widehat{ACM}=40^{\circ}}$

Exercice 28
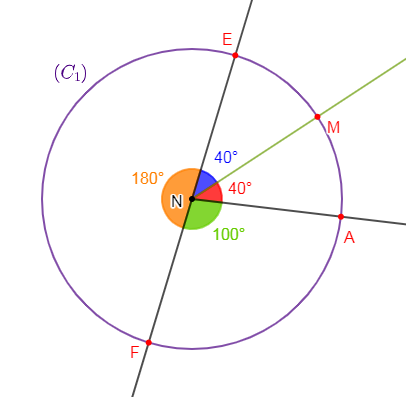
1) Traçons un angle $\widehat{MNE}$ tel que $\widehat{MNE}=40^{\circ}\ $ et $\ NE=NM=3\;cm.$
2) Traçons le cercle $(C_{1})$ de centre $N$ et de rayon $NM.$
3) Plaçons le point $A$ sur le cercle $(C_{1})$ tel que $\widehat{MNA}=40^{\circ}.$
La droite $(NM)$ est la bissectrice de l'angle $\widehat{ANE}.$
En observant la figure, on constate que la droite $(NM)$, passant par le sommet $N$ de l'angle $\widehat{ANE}$, partage cet angle en deux angles de même mesure.
Donc, cette droite représente la bissectrice de l'angle $\widehat{ANE}.$
4) Plaçons le point $F$ sur le cercle $(C_{1})$ tel que les points $E\;,\ N\ $ et $\ F$ soient alignés.
a) La mesure de l'angle $\widehat{FNE}$ est égale à $180^{\circ}.$
Justifions notre réponse.
Comme les points $E\;,\ N\ $ et $\ F$ soient alignés alors, l'angle $\widehat{FNE}$ est un angle plat.
Donc, sa mesure est égale à $180^{\circ}.$
b) Calculons la mesure de l'angle $\widehat{FNA}.$
On a : les angles $\widehat{FNA}\ $ et $\ \widehat{ANE}$ sont supplémentaires.
Donc,
$$mes\;\widehat{FNA}+mes\;\widehat{ANE}=180^{\circ}$$
Ce qui entraine : $mes\;\widehat{FNA}=180^{\circ}-mes\;\widehat{ANE}$
Mais, on sait que : $(NM)$ est la bissectrice de l'angle $\widehat{ANE}.$
Donc, $mes\;\widehat{ANE}=2\times 40^{\circ}=80^{\circ}$
On remplace alors $mes\;\widehat{ANE}$ par sa valeur $80^{\circ}.$
On obtient :
$\begin{array}{rcl} mes\;\widehat{FNA}&=&180^{\circ}-mes\;\widehat{ANE}\\\\&=&180^{\circ}-80^{\circ}\\\\&=&100^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{FNA}$ est égale à $100^{\circ}.$

Exercice 29
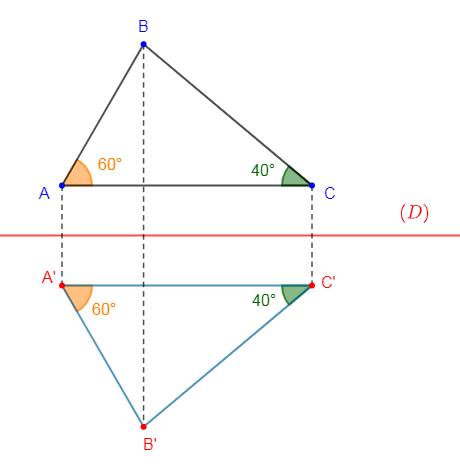
Reproduisons la figure puis construisons le symétrique du triangle $ABC$ par rapport à la droite.
On construit alors $A'\;;\ B'\ $ et $\ C'$ symétriques respectifs des points $A\;;\ B\ $ et $\ C$ par rapport à la droite $(D)$ puis on trace le triangle $A'B'C'.$ C'est le symétrique du triangle $ABC$ par rapport à la droite $(D).$

Exercice 30
Sur la figure codée ci-dessous :

1) $\widehat{AHB}\ $ et $\ \widehat{HBF}$ sont deux angles aigus.
Le codage montre que la mesure des angles $\widehat{AHB}\ $ et $\ \widehat{HBF}$ est inférieure à $90^{\circ}$ donc, $\widehat{AHB}\ $ et $\ \widehat{HBF}$ sont deux angles aigus.
2) $\widehat{ABF}$ est un angle obtus.
Le codage montre que la mesure de l'angle $\widehat{ABF}$ est supérieure à $90^{\circ}$ donc, $\widehat{ABF}$ est un angle obtus.
3) $\widehat{AHB}\ $ et $\ \widehat{HBA}$ sont deux angles complémentaires.
On a : $ABH$ es un triangle rectangle en $A$ donc, ses angles aigus sont complémentaires.
Ce qui signifie que $\widehat{AHB}\ $ et $\ \widehat{HBA}$ sont deux anges complémentaires.
4) $\widehat{EFH}\ $ et $\ \widehat{BEG}$ sont deux angles supplémentaires.
On a : $mes\;\widehat{EFH}+mes\;\widehat{BEG}=90^{\circ}+90^{\circ}=180^{\circ}$
Donc, $\widehat{EFH}\ $ et $\ \widehat{BEG}$ sont deux angles supplémentaires.
Exercice 31
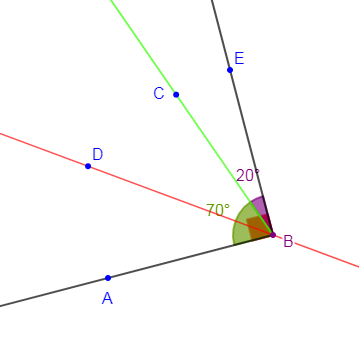
1) Construisons un angle droit $\widehat{ABE}$ puis traçons la demi-droite $[BC)$ telle que $\widehat{EBC}=20^{\circ}\ $ et $\ \widehat{EBC}$ adjacent à $\widehat{CBA}.$
2) Construisons la demi-droite $[BD)$ bissectrice de l'angle $\widehat{CBA}.$
3) Calculons la mesure l'angle $\widehat{CBA}.$
On a : $\widehat{EBC}\ $ et $\ \widehat{CBA}$ sont deux angles adjacents.
Donc, $mes\;\widehat{EBC}+mes\;\widehat{CBA}=mes\;\widehat{ABE}$
Or, $\widehat{ABE}$ est un angle droit donc, sa mesure est égale à $90^{\circ}.$
Ainsi, on a : $mes\;\widehat{EBC}+mes\;\widehat{CBA}=90^{\circ}$
Ce qui entraine alors : $mes\;\widehat{CBA}=90^{\circ}-mes\;\widehat{EBC}$
En remplaçant $mes\;\widehat{EBC}$ par sa valeur $20^{\circ}$, on obtient :
$\begin{array}{rcl} mes\;\widehat{CBA}&=&90^{\circ}-mes\;\widehat{EBC}\\\\&=&90^{\circ}-20^{\circ}\\\\&=&70^{\circ}\end{array}$
Donc, la mesure de l'angle $\widehat{CBA}$ est égale à $70^{\circ}.$
4) Déterminons la mesure des angles $\widehat{DBA}\ $ et $\ \widehat{DBC}$ en justifiant notre réponse.
On a : $[BD)$ est bissectrice de l'angle $\widehat{CBA}.$
Donc, la demi-droite $[BD)$ partage l'angle $\widehat{CBA}$ en deux angles de même mesure.
Ce qui signifie que :
$$mes\;\widehat{DBA}=mes\;\widehat{DBC}=\dfrac{mes\;\widehat{CBA}}{2}$$
En remplaçant $mes\;\widehat{CBA}$ par sa valeur $70^{\circ}$, on trouve :
$mes\;\widehat{DBA}=mes\;\widehat{DBC}=\dfrac{70^{\circ}}{2}=35^{\circ}$
Ainsi, la mesure des angles $\widehat{DBA}\ $ et $\ \widehat{DBC}$ est égale à $35^{\circ}.$

Auteur:
Diny Faye

Ajouter un commentaire