Solution des exercices : Vecteurs et translations - 4e
Classe:
Quatrième
Exercice 1
Soit $ABCD$ un parallélogramme de centre $O.$
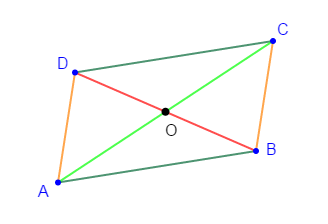
Parmi les vecteurs suivants :
$$\overrightarrow{AB}\;;\ \overrightarrow{BC}\;;\ \overrightarrow{CD}\;;\ \overrightarrow{DA}\;;\ \overrightarrow{AC}\;;\ \overrightarrow{BD}\;;\ \overrightarrow{AO}\;;\ \overrightarrow{OC}\;;\ \overrightarrow{DO}\ \text{ et }\ \overrightarrow{OB}$$
a) Ceux de même direction sont :
$\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$
$\overrightarrow{BC}\ $ et $\ \overrightarrow{DA}$
$\overrightarrow{AC}\;;\ \overrightarrow{AO}\ $ et $\ \overrightarrow{OC}$
$\overrightarrow{BD}\;;\ \overrightarrow{DO}\ $ et $\ \overrightarrow{OB}$
b) Ceux de même sens sont :
$\overrightarrow{AC}\;;\ \overrightarrow{AO}\ $ et $\ \overrightarrow{OC}$
$\overrightarrow{DO}\ $ et $\ \overrightarrow{OB}$
c) Ceux de même longueur sont :
$\overrightarrow{AB}\ $ et $\ \overrightarrow{CD}$
$\overrightarrow{BC}\ $ et $\ \overrightarrow{DA}$
$\overrightarrow{AO}\ $ et $\ \overrightarrow{OC}$
$\overrightarrow{DO}\ $ et $\ \overrightarrow{OB}$
d) Ceux qui sont égaux sont :
$\overrightarrow{AO}\ $ et $\ \overrightarrow{OC}$
$\overrightarrow{DO}\ $ et $\ \overrightarrow{OB}$
Exercice 2
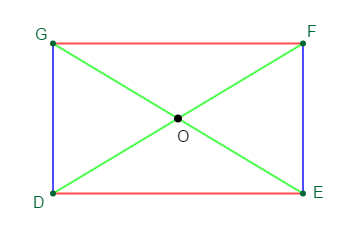
Soit $DEFG$ un rectangle alors, les égalités suivantes sont fausses : $$\overrightarrow{GD}=\overrightarrow{EG}\;;\ \overrightarrow{DF}=\overrightarrow{EG}\;;\ \overrightarrow{DE}=\overrightarrow{FG}$$
En effet, on sait que deux vecteurs sont égaux si ils sont de même direction, de même sens et de même longueur.
Or, $\overrightarrow{GD}\ $ et $\ \overrightarrow{EG}$ ne sont ni de même direction, ni de même sens, ni de même longueur. Donc, il ne sont pas égaux.
Aussi, comme $DEFG$ un rectangle alors, les diagonales ont même longueur. Donc, $\overrightarrow{EG}\ $ et $\ \overrightarrow{DF}$ sont de même longueur. Mais, on constate qu'ils ne sont ni de même direction, ni de même sens. Par suite, ces deux vecteurs ne sont pas égaux.
Par ailleurs, $\overrightarrow{DE}\ $ et $\ \overrightarrow{FG}$ sont de même direction et de même longueur mais sont de sens différent donc, ils ne sont pas égaux.
Exercice 3 Image d'un segment
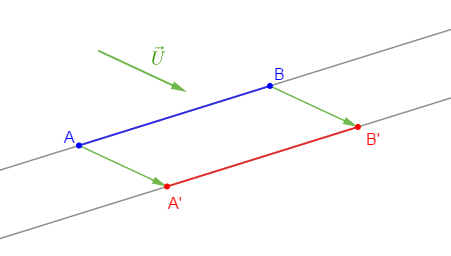
Soit $\vec{U}$ un vecteur du plan
1) Construisons un segment $[AB]$ tel que $AB=4\;cm.$
2) Construisons les points $A'\ $ et $\ B'$ image respectif de $A\ $ et $\ B$ par la translation de vecteur $\vec{U}.$
3) a) Déterminons la longueur de $A'B'$
On a : $A'B'=AB$ or, $AB=4\;cm$
Donc, $\boxed{A'B'=4\;cm}$
b) $(AB)\ $ et $\ (A'B')$ sont parallèles
4) Énonçons la propriété.
L'image d'un segment par une translation est un segment de même longueur et qui lui est parallèle.
Exercice 4
On donne trois points non alignés $A\;;\ B\;;\ C.$
1) Construisons les points $M\ $ et $\ N$ tels que : $\overrightarrow{BC}=\overrightarrow{AM}\ $ et $\ \overrightarrow{BN}=\overrightarrow{AC}.$
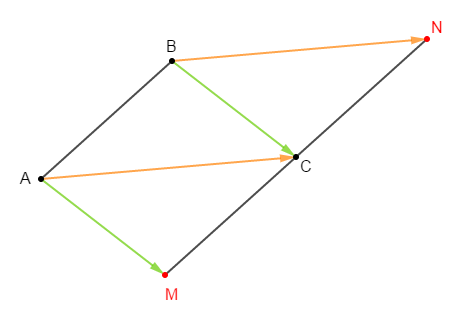
2) Démontrons que $C$ est le milieu du segment $[MN].$
En effet, comme $\overrightarrow{BC}=\overrightarrow{AM}$ alors, $BCMA$ est un parallélogramme.
Par suite, $\overrightarrow{AB}=\overrightarrow{MC}$
Aussi, on a : $\overrightarrow{BN}=\overrightarrow{AC}$ donc, $BNCA$ est un parallélogramme.
Alors, $\overrightarrow{AB}=\overrightarrow{CN}$
Ainsi, on obtient : $\left\lbrace\begin{array}{rcl} \overrightarrow{AB}&=&\overrightarrow{MC}\\\\\overrightarrow{AB}&=&\overrightarrow{CN}\end{array}\right.$
Ce qui donne alors : $\overrightarrow{MC}=\overrightarrow{CN}$
D'où, $C$ est le milieu du segment $[MN].$
Exercice 5
$ABCD$ est un parallélogramme
1) Construisons le point $E$ image de $C$ par la translation de vecteur $\overrightarrow{DC}.$
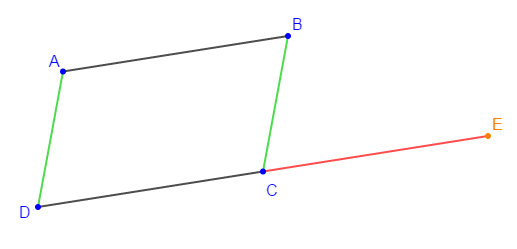
2) a) Expliquons pourquoi on a : $\overrightarrow{AB}=\overrightarrow{DC}\ $ et $\ \overrightarrow{CE}=\overrightarrow{DC}$
En effet, comme $ABCD$ est un parallélogramme alors, on a :
$$\overrightarrow{AB}=\overrightarrow{DC}$$
Par ailleurs, comme $t_{\overrightarrow{DC}}(C)=E$ alors, cela signifie que les vecteurs $\overrightarrow{CE}\ $ et $\overrightarrow{DC}$ sont de même direction, de même sens et de même longueur.
Par conséquent, ils sont égaux. D'où,
$$\overrightarrow{CE}=\overrightarrow{DC}$$
b) En déduisons que $\overrightarrow{AB}=\overrightarrow{CE}.$
En effet, d'après le résultat de 2) a), on a :
$$\left\lbrace\begin{array}{rcl} \overrightarrow{AB}&=&\overrightarrow{DC}\\\\\overrightarrow{CE}&=&\overrightarrow{DC}\end{array}\right.$$
Ce qui entraine alors :
$$\overrightarrow{AB}=\overrightarrow{CE}$$
Exercice 6
Soit $MNP$ un triangle isocèle en $M.$ on désigne par $M'$ le milieu de $[NP].$
Soit $Q$ le point tel que : $\overrightarrow{M'Q}=\overrightarrow{MM'}.$
1) Démontrons que $(MM')$ est la médiatrice de $[NP].$
Comme $MNP$ est un triangle isocèle en $M\ $ et $\ M'$ est le milieu de $[NP]$ alors, la droite $(MM')$ est un axe de symétrie de ce triangle.
Par conséquent, elle est perpendiculaire à $(NP)$ et coupe $[NP]$ par le milieu.
Ce qui signifie alors que $(MM')$ est la médiatrice de $[NP].$
2) Démontrons que le quadrilatère $MNQP$ est un losange.
En effet, comme $\overrightarrow{M'Q}=\overrightarrow{MM'}$ alors, $M'$ est milieu de $[MQ].$
Or, on sait aussi que $M'$ est le milieu de $[NP].$
Donc, $[MQ]\ $ et $\ [NP]$ ont même milieu.
Ainsi, le quadrilatère $MNQP$ a ses diagonales de même milieu donc, c'est un parallélogramme.
Par ailleurs, d'après le résultat de $1)$, on a : $(MM')$ perpendiculaire à $(MQ).$
Ce qui signifie que le parallélogramme $MNQP$ a ses diagonales perpendiculaires.
Par conséquent, $MNQP$ est un losange.
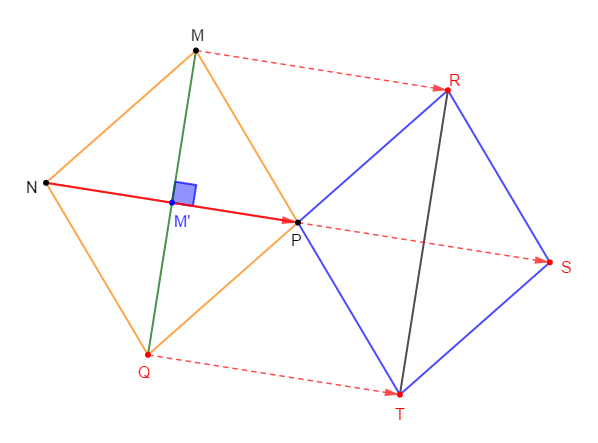
3) Construisons l'image de $MNQP$ par la translation de vecteur $\overrightarrow{NP}.$
Pour cela, nous allons construire l'image de chaque sommet du losange $MNQP$ par la translation $t_{\overrightarrow{NP}}.$
Ainsi, on a :
$$\left.\begin{array}{rcl} t_{\overrightarrow{NP}}(M)&=&R\\\\t_{\overrightarrow{NP}}(N)&=&P\\\\t_{\overrightarrow{NP}}(Q)&=&T\\\\t_{\overrightarrow{NP}}(P)&=&S\end{array}\right\rbrace\ \Rightarrow\ t_{\overrightarrow{NP}}(MNQP)=RPTS$$
Remarque :
l'image d'une figure géométrique par une translation de vecteur est une figure géométrique de même nature.
Ainsi, $RPTS$ est aussi un losange.
Exercice 7
Soit $(\mathcal{C})$ un cercle de centre $O$ de diamètre $[AB]\ $ et $\ M$ un point de ce cercle.
1) Déterminons la nature du triangle $AMB$
$AMB$ est un triangle rectangle en $M.$
Justifions
En effet, le triangle $AMB$ est inscrit dans le cercle $(\mathcal{C})$ avec son côté $[AB]$ qui est un diamètre de ce cercle.
Par conséquent, c'est un triangle rectangle en $M.$
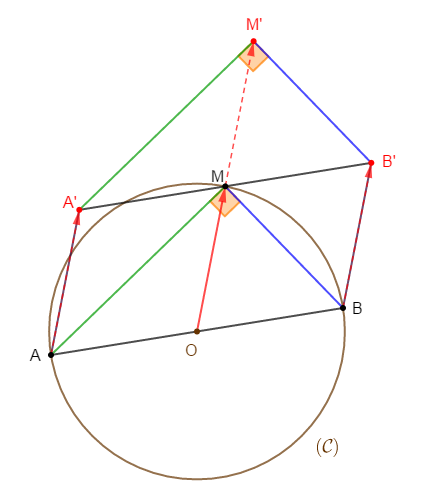
2) a) Construisons les points $A'\;,\ B'\;,\ M'$ images respectives de $A\;,\ B\;,\ M$ par la translation de vecteur $\overrightarrow{OM}.$
b) L'image de $O$ par la translation de vecteur $\overrightarrow{OM}$ est le point $M.$
3) Le quadrilatère $ABB'A'$ est un parallélogramme.
En effet, on a :
$t_{\overrightarrow{OM}}(A)=A'\ \Rightarrow\ \overrightarrow{OM}=\overrightarrow{AA'}$
$t_{\overrightarrow{OM}}(B)=B'\ \Rightarrow\ \overrightarrow{OM}=\overrightarrow{BB'}$
Ce qui donne alors, $\overrightarrow{AA'}=\overrightarrow{BB'}$
D'où, $ABB'A'$ est un parallélogramme.
4) a) Démontrons que $A'B'M'$ est un triangle rectangle.
Comme les points $A'\;,\ B'\;,\ M'$ sont les images respectives de $A\;,\ B\;,\ M$ par la translation de vecteur $\overrightarrow{OM}$ alors, le triangle $A'M'B'$ est l'image du triangle $AMB$ par cette même translation.
Or, on sait que l'image d'un triangle par une translation de vecteur est un triangle de même nature.
Par conséquent, $A'B'M'$ est un triangle rectangle en $M'.$
b) On donne : $OB=5\;cm\ $ et $\ MB=6\;cm.$ Calculons $AM$
Comme $AMB$ est rectangle en $M$ alors, en appliquant le théorème de Pythagore, on a :
$$AM^{2}+MB^{2}=AB^{2}$$
Ce qui donne : $AM^{2}=AB^{2}-MB^{2}$
Or, on sait que $[AB]$ est un diamètre de $(\mathcal{C})$ donc, $AB=2OB$
Ainsi, en remplaçant $AB$ par $2OB$, on obtient :
$\begin{array}{rcl} AM^{2}&=&AB^{2}-MB^{2}\\\\&=&(2OB)^{2}-MB^{2}\\\\&=&(2\times 5)^{2}-6^{2}\\\\&=&10^{2}-36\\\\&=&100-36\\\\&=&64\end{array}$
Donc, $AM^{2}=64$
Comme $64=8^{2}$ alors, on a : $AM^{2}=8^{2}$
D'où, $\boxed{AM=8\;cm}$
En déduisons l'aire du triangle $A'B'M'.$
Comme $A'B'M'$ est identique à $AMB$ alors, l'aire du triangle $A'B'M'$ sera égale à celle du triangle $AMB.$
Soit alors : $\mathcal{A}$ l'aire du triangle $AMB.$
On a :
$\begin{array}{rcl} \mathcal{A}&=&\dfrac{AM\times MB}{2}\\\\&=&\dfrac{8\times 6}{2}\\\\&=&\dfrac{48}{2}\\\\&=&24\end{array}$
Donc, $\boxed{\mathcal{A}=24\;cm^{2}}$
Ainsi, l'aire du triangle $A'B'M'$ est égale à $24\;cm^{2}.$
Exercice 8
Soit $ABC$ un triangle rectangle en $A$ tel que : $AB=3\;cm\ $ et $\ AC=4\;cm.$
1) Calculons la distance $BC$
Comme le triangle $AC$ est rectangle en $A$ alors, en appliquant le théorème de Pythagore, on a :
$$BC^{2}=AB^{2}+AC^{2}$$
Ainsi, en remplaçant $AB\ $ et $\ AC$ par leur valeur, on obtient :
$\begin{array}{rcl} BC^{2}&=&AB^{2}+AC^{2}\\\\&=&3^{2}+4^{2}\\\\&=&9+16\\\\&=&25\end{array}$
Donc, $BC^{2}=25$
Comme $25=5^{2}$ alors, on a : $BC^{2}=5^{2}$
D'où, $\boxed{BC=5\;cm}$
2) Soit $I$ milieu du segment $[AC].$
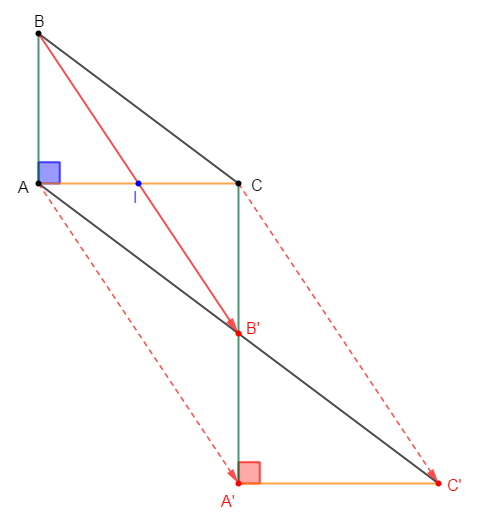
a) Construisons le point $B'$ tel que : $\overrightarrow{BI}=\overrightarrow{IB'}$
b) Démontrons que $ABCB'$ est un parallélogramme.
On a : $\overrightarrow{BI}=\overrightarrow{IB'}.$ Ce qui signifie que $I$ est milieu de $[BB'].$
Or, on sait aussi que $I$ est milieu de $[AC].$
Donc, le quadrilatère $ABCB'$ a ses diagonales de même milieu.
Par conséquent, c'est un parallélogramme.
3) Construisons :
$-\ C'$ image de $C$ par la translation de vecteur $\overrightarrow{BB}'$
$-\ A'$ image de $A$ par la translation de vecteur $\overrightarrow{BB}'.$
4) a) Le vecteur de translation qui envoie $ABC\ $ en $\ A'B'C'$ est le vecteur $\overrightarrow{BB'}$
b) Donnons la nature du triangle $A'B'C'$
En effet, le triangle $A'B'C'$ est l'image du triangle $ABC$ par la translation de vecteur $\overrightarrow{BB'}.$
Or, on sait que l'image d'un triangle par une translation de vecteur est un triangle de même nature.
Par conséquent, $A'B'C'$ est un triangle rectangle en $A'.$
Calculons son aire
Comme les deux triangles sont identique alors, l'aire du triangle $A'B'C'$ sera égale à celle du triangle $ABC.$
Soit alors : $\mathcal{A}$ l'aire du triangle $ABC.$
On a :
$\begin{array}{rcl} \mathcal{A}&=&\dfrac{AB\times AC}{2}\\\\&=&\dfrac{3\times 4}{2}\\\\&=&\dfrac{12}{2}\\\\&=&6\end{array}$
Donc, $\boxed{\mathcal{A}=6\;cm^{2}}$
Ainsi, l'aire du triangle $A'B'C'$ est égale à $6\;cm^{2}.$
5) Démontrons que $B'$ est le milieu de $[A'C].$
En effet, on a :
$t_{\overrightarrow{BB'}}(A)=A'\ \Rightarrow\ \overrightarrow{BB'}=\overrightarrow{AA'}$
$t_{\overrightarrow{BB'}}(C)=C'\ \Rightarrow\ \overrightarrow{BB'}=\overrightarrow{CC'}$
Ce qui entraine alors, $\overrightarrow{AA'}=\overrightarrow{CC'}$
D'où, $ACC'A'$ est un parallélogramme.
Par conséquent, ses diagonales $[AC']\ $ et $\ [A'C]$ se coupent en leur milieu.
Ainsi, $B'$ est milieu de $[A'C].$
Exercice 9
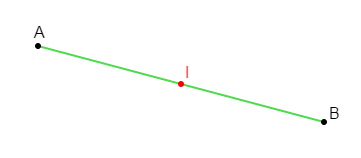
Soit un segment $[AB]\ $ et $\ I$ son milieu.
1) Les points $A\;,\ I\ $ et $\ B$ sont alignés.
En effet, $I$ est milieu de $[AB]$ donc, $I\in[AB].$ Ce qui signifie que $A\;,\ I\ $ et $\ B$ sont alignés dans cet ordre.
2) Comparons les longueurs $AI\ $ et $\ IB.$
Comme $I$ est milieu de $[AB]$ alors, on a :
$$AI=IB$$
3) L'image de $I$ par la translation qui transforme $A\ $ en $\ I$ est le point $B.$
En effet, comme $I$ est milieu de $[AB]$ alors, on a :
$$\overrightarrow{AI}=\overrightarrow{IB}$$
Ce qui se traduit par : $t_{\overrightarrow{AI}}(I)=B$
Exercice 10
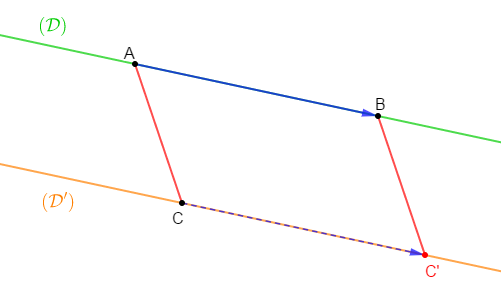
1) Traçons deux droites $(\mathcal{D})\ $ et $\ (\mathcal{D'})$ parallèles puis marquons deux points $A\ $ et $\ B$ sur $(\mathcal{D})$ et un point $C$ sur $(\mathcal{D'}).$
2) Construisons le point $C'$ tel que $ABC'C$ soit un parallélogramme.
3) La translation de vecteur $\overrightarrow{AB}$ transforme $C$ en $C'.$
En effet, comme $ABC'C$ est un parallélogramme alors, on a :
$$\overrightarrow{AB}=\overrightarrow{CC'}$$
Ce qui peut s'écrire : $t_{\overrightarrow{AB}}(C)=C'$
Ainsi, la translation de vecteur $\overrightarrow{AB}$ transforme $C$ en $C'.$
Exercice 11
Répondons par vrai ou faux à chacune des affirmations ci-dessous :
Soit un vecteur $\overrightarrow{EF}\ $ et $\ O$ un point du plan.
1) Si $\overrightarrow{OE}=\overrightarrow{FE}$ alors, $O$ est le milieu du segment $[EF].\quad\text{Faux}$
2) Si $\overrightarrow{EO}=\overrightarrow{OF}$ alors; $O$ est le milieu du segment $[EF].\quad\text{Vrai}$
3) Si $\overrightarrow{EO}=\overrightarrow{FO}$ alors, $O$ est le milieu du segment $[EF].\quad\text{Faux}$
4) Si $\overrightarrow{OE}=\overrightarrow{OF}$ alors, $O$ est le milieu du segment $[EF].\quad\text{Faux}$
Exercice 12
Recopions puis complétons les phrases ci-dessous.
1) Si trois points sont alignés alors leurs images par une translation sont alignées.
2) L'image d'un segment par une translation est un segment de même longueur et qui lui est parallèle.
3) L'image d'une droite par une translation est une droite qui lui est parallèle.
4) L'image d'un cercle par une translation est un cercle de même rayon et de centre l'image du centre du cercle.
5) L'image d'un angle par une translation est un angle de même mesure
Exercice 13
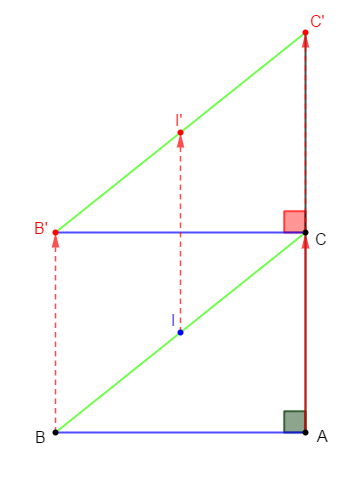
$ABC$ est un triangle rectangle en $A$ tel que $AB=5\;cm\ $ et $\ AC=4\;cm.$
Soit $I$ le milieu de $[BC]$
1) Construisons les points $B'\;,\ C'\ $ et $\ I'$ images respectives des points $B\;,\ C\ $ et $\ I$ par la translation qui transforme $A$ en $C.$
2) Déterminons la longueur du segment $[B'C']$
On sait que l'image d'un segment par une translation de vecteur est un segment de même longueur.
Or, $[B'C']$ est l'image de $[BC]$ par la translation de vecteur $\overrightarrow{AC}.$
Donc, $B'C'=BC$
Calculons alors la longueur $BC.$
Comme $ABC$ est un triangle rectangle en $A$ alors, en appliquant le théorème de Pythagore, on a :
$$BC^{2}=AB^{2}+AC^{2}$$
Ainsi, en remplaçant $AB\ $ et $\ AC$ par leur valeur, on obtient :
$\begin{array}{rcl} BC^{2}&=&AB^{2}+AC^{2}\\\\&=&5^{2}+4^{2}\\\\&=&25+16\\\\&=&41\end{array}$
Donc, $BC^{2}=41$
Comme $41\approx(6.4)^{2}$ alors, on a : $BC^{2}\approx(6.4)^{2}$
D'où, $\boxed{BC\approx 6.4\;cm}$
Ainsi, la longueur du segment $[BC]$ est approximativement égale à $6.4\;cm$
3) Les trois points $B'\;,\ I'\ $ et $\ C'$ sont alignés.
En effet, on sait que les images de points alignés par une translation de vecteur sont des points alignés.
Or, $I$ est le milieu de $[BC]$ donc, les points $B\;,\ I\ $ et $\ C$ sont alignés.
Par conséquent, leurs images $B'\;,\ I'\ $ et $\ C'$, par la translation de vecteur $\overrightarrow{AC}$, sont aussi des points alignés.
4) La mesure de l'angle $\widehat{B'CC'}$ est de : $90^{\circ}$
En effet, on sait que l'image d'un angle par une translation de vecteur est un angle de même mesure.
Or, l'angle $\widehat{BAC}$ a pour mesure $90^{\circ}\ $ et $\ \widehat{B'CC'}$ est l'image de $\widehat{BAC}$ par la translation de vecteur $\overrightarrow{AC}$
Par conséquent, $\widehat{B'CC'}=90^{\circ}.$

Exercice 14
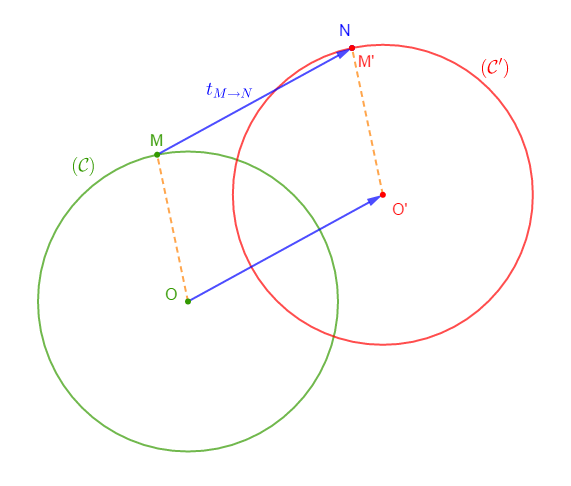
Soit le cercle $\mathcal{C}(O\;;\ 3\;cm).$
1) Marquons un point $M$ sur le cercle et un point $N$ à l'extérieur du cercle.
2) Construisons les points $O'\ $ et $M'\ $ images respectives des points $O\ $ et $\ M$ par la translation qui transforme $M$ en $N.$
Soit $t_{M\rightarrow N}$ la translation qui transforme $M$ en $N$ alors, on a :
$t_{M\rightarrow N}(O)=O'\ \Rightarrow\ \overrightarrow{MN}=\overrightarrow{OO'}$
$t_{M\rightarrow N}(M)=M'\ \Rightarrow\ \overrightarrow{MN}=\overrightarrow{MM'}$ Donc, $M'=N$
3) Construisons le cercle $(\mathcal{C'})$ de centre $O'$ et de rayon $O'M'.$
4) Montrons que $(\mathcal{C'})$ est l'image de $(\mathcal{C})$ par la translation qui transforme $M$ en $N.$
On a : le cercle $(\mathcal{C'})$ passe par $M'$ image de $M\in(\mathcal{C})$ et son centre $O'$ est image de $O$ centre du cercle $(\mathcal{C})$, par la translation $t_{M\rightarrow N}.$
Par conséquent, $(\mathcal{C'})$ est l'image de $(\mathcal{C})$ par la translation $t_{M\rightarrow N}$ qui transforme $M$ en $N.$
Exercice 15
Répondons par vrai ou faux à chacune des affirmations ci-dessous.
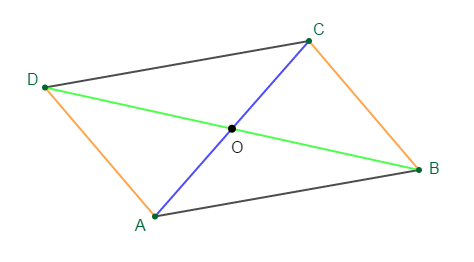
1) Si $ABCD$ est un parallélogramme alors, $\overrightarrow{AB}=\overrightarrow{CD}.\quad\text{Faux}$
2) Si $ABCD$ est un parallélogramme alors, $\overrightarrow{AD}=\overrightarrow{BC}.\quad\text{Vrai}$
3) Si $ABCD$ est un parallélogramme alors, $\overrightarrow{AC}=\overrightarrow{BD}.\quad\text{Faux}$
4) Si $ABCD$ est un parallélogramme alors, $\overrightarrow{DA}=\overrightarrow{BC}.\quad\text{Faux}$
5) Si $ABCD$ est un parallélogramme alors, $\overrightarrow{CD}=\overrightarrow{BA}.\quad\text{Vrai}$

Exercice 16
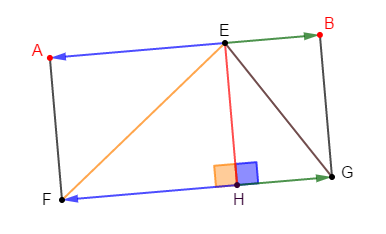
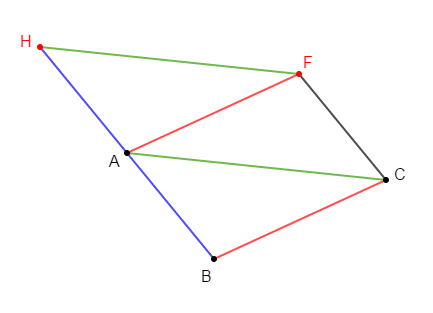
1) Construisons un triangle $EFG$, puis les points $H\;,\ A\;,\ B$ tels que :
$H$ pied de la hauteur issue de $E$ ;
$A$ l'image de $E$ par la translation de vecteur $\overrightarrow{HF}$ ;
$B$ l'image de $E$ par la translation de vecteur $\overrightarrow{HG}$ ;
2) Donnons la nature des quadrilatères $BEHG\ $ et $\ HFAE.$
Comme $A$ l'image de $E$ par la translation de vecteur $\overrightarrow{HF}$ alors, on a :
$$\overrightarrow{HF}=\overrightarrow{EA}$$
Par suite, le quadrilatère $HFAE$ est un parallélogramme.
De plus, $H$ étant pied de la hauteur issue de $E$ donc, $(EH)$ est perpendiculaire à $(HF)$ en $H.$
Ainsi, le parallélogramme $HFAE$ a un angle droit.
Par conséquent, c'est un rectangle.
De la même manière, on a : $B$ image de $E$ par la translation de vecteur $\overrightarrow{HG}$ donc,
$$\overrightarrow{HG}=\overrightarrow{EB}$$
Ce qui signifie que le quadrilatère $BEHG$ est un parallélogramme.
Comme $H$ est le pied de la hauteur issue de $E$ alors, $(EH)$ est perpendiculaire à $(HG)$ en $H.$
Donc, le parallélogramme $BEHG$ a un angle droit.
Par conséquent, c'est un rectangle.
Exercice 17
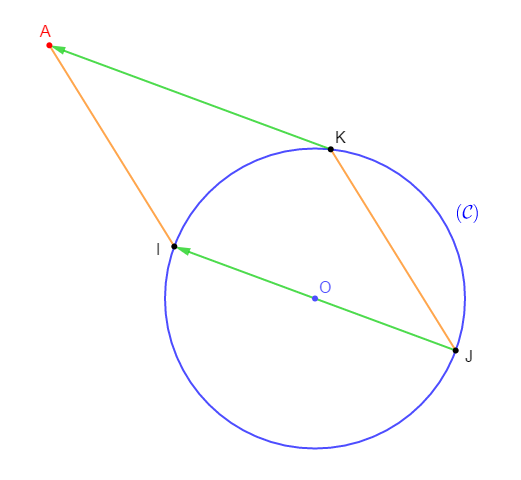
1) Construisons un cercle $\mathcal{C}(O\;;\ 3\;cm).$
2) Marquons les points $I\;,\ J\ $ et $\ K$ sur $(\mathcal{C})$ tels que les points $I\ $ et $\ J$ soient diamétralement opposés.
3) Construisons le point $A$ l'image de $K$ par la translation de vecteur $\overrightarrow{JI}.$
4) Le quadrilatère $AIJK$ est un parallélogramme.
En effet, on a : $A$ image de $K$ par la translation de vecteur $\overrightarrow{JI}.$
Ce qui donne alors :
$$\overrightarrow{JI}=\overrightarrow{KA}$$
D'où, le quadrilatère $AIJK$ est un parallélogramme.
Exercice 18
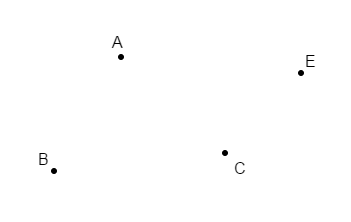
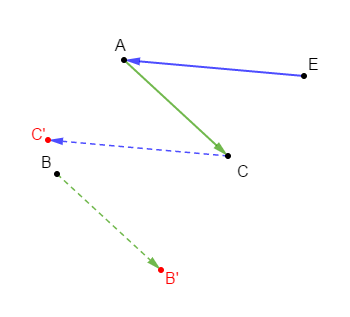
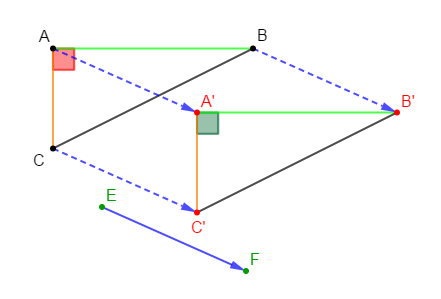
Reproduisons la figure ci-dessus puis :
$-\ $ construisons le point $B'$ image de $B$ par la translation qui transforme $A$ en $C$ ;
Méthode :
On construit d'abord le vecteur $\overrightarrow{AC}$ et ensuite, on place le point $B'$ tel que : $\overrightarrow{AC}=\overrightarrow{BB'}$
$-\ $ construisons le point $C'$ image de $C$ par la translation qui transforme $E$ en $A$
Méthode :
On trace d'abord le vecteur $\overrightarrow{EA}$ et ensuite, on construit le point $C'$ tel que : $\overrightarrow{EA}=\overrightarrow{CC'}$
Exercice 19
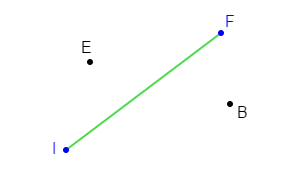
Reproduisons la figure ci-dessus puis construisons l'image du segment $[IF]$ par la translation qui transforme $E$ en $B.$
Méthode :
On trace d'abord le vecteur $\overrightarrow{EB}.$
Ensuite, on place les points $I'\ $ et $\ F'$ tels que : $\overrightarrow{EB}=\overrightarrow{II'}\ $ et $\ \overrightarrow{EB}=\overrightarrow{FF'}$
Enfin, on trace le segment $[I'F'].$
Le segment $[I'F']$ est donc l'image du segment $[IF]$ par la translation qui transforme $E$ en $B.$
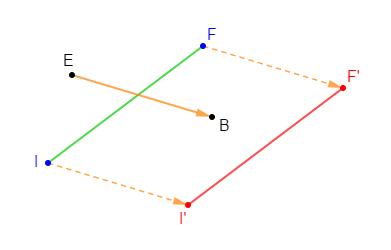
Exercice 20
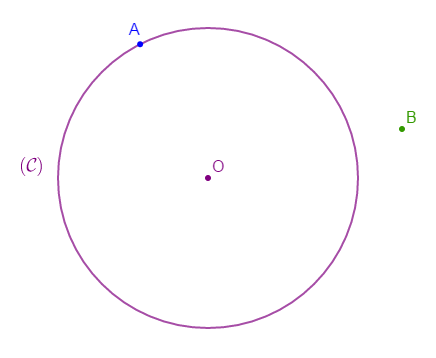
Reproduisons la figure ci-dessus puis construisons l'image du cercle $(\mathcal{C})$ de centre $O$ et de rayon $3\;cm$ par la translation qui transforme $B$ en $A.$
Méthode :
On trace d'abord le vecteur $\overrightarrow{BA}.$
Ensuite, on place les points $A'\ $ et $\ O'$ tels que : $\overrightarrow{AA'}=\overrightarrow{BA}\ $ et $\ \overrightarrow{OO'}=\overrightarrow{BA}$
Enfin, on trace le cercle $(\mathcal{C}')$ de centre $O'$ et passant par $A'.$
$(\mathcal{C}')$ est donc l'image du cercle $(\mathcal{C})$ par la translation qui transforme $B$ en $A.$
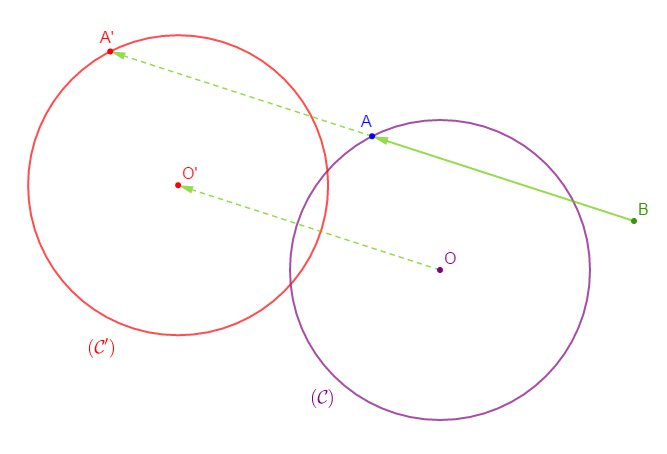
Exercice 21
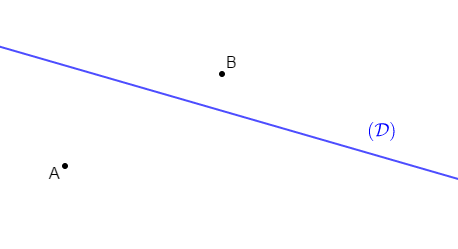
Reproduisons la figure ci-dessus puis construisons l'image $(\mathcal{D'})$ de la droite $(\mathcal{D})$ par la translation qui transforme $A$ en $B.$
Méthode :
On trace d'abord le vecteur $\overrightarrow{AB}.$
Ensuite, on place deux points $C\ $ et $\ D$ sur la droite $(\mathcal{D})$ puis, on place leurs images respectives $C'\ $ et $\ D'$ par la translation de vecteur $\overrightarrow{AB}.$
Enfin, on trace la droite $(\mathcal{D}')$ passant par $C'\ $ et $\ D'.$
Cette droite $(\mathcal{D}')$ est donc l'image de la droite $(\mathcal{D})$ par la translation qui transforme $A$ en $B.$
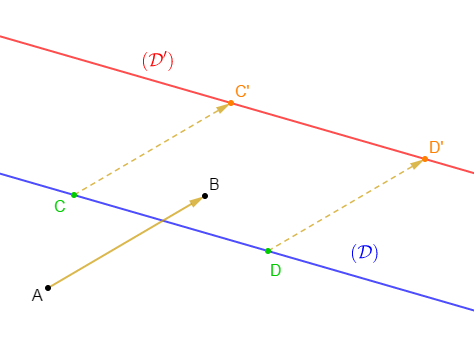
Exercice 22
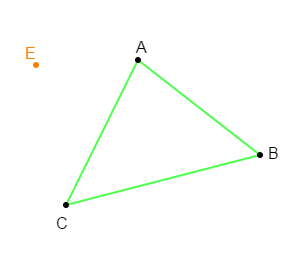
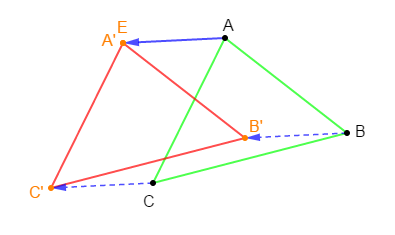
Reproduisons la figure ci-dessus puis construisons l'image $A'B'C'$ du triangle $ABC$ par la translation qui transforme $A$ en $E.$
Méthode :
On trace d'abord le vecteur $\overrightarrow{AE}.$
Ensuite, on place les points $A'\;,\ B'\ $ et $\ C'$ tels que : $\overrightarrow{AA'}=\overrightarrow{AE}\;,\ \overrightarrow{BB'}=\overrightarrow{AE}\ $ et $\ \overrightarrow{CC'}=\overrightarrow{AE}.$
Enfin, on trace le triangle $A'B'C'.$
Le triangle $A'B'C'$ est donc l'image du triangle $ABC$ par la translation qui transforme $A$ en $E.$
Exercice 23
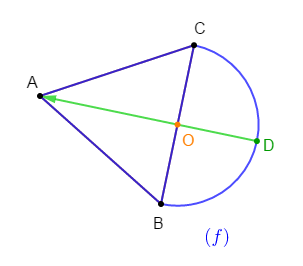
Dans la figure $(f)$ ci-dessous, $ABC$ est un triangle équilatéral et $O$ est le centre du demi-cercle de diamètre $[BC].$
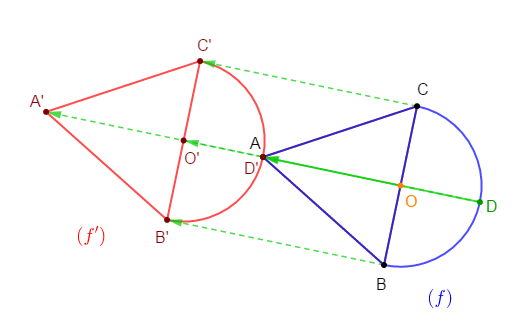
1) Reproduisons la figure $(f)$
2) Construisons l'image $(f')$ de $(f)$ par la translation de vecteur $\overrightarrow{DA}.$
3) Justifions que $A'\;,\ O'\ $ et $\ D'$ images respectives de $A\;,\ O\ $ et $\ D$ par cette translation de vecteur $\overrightarrow{DA}.$ sont alignés.
En effet, on sait que : les images de points alignés par une translation de vecteur sont des points alignés.
Or, les points $A\;,\ O\ $ et $\ D$ sont alignés.
Par conséquent, leurs images $A'\;,\ O'\ $ et $\ D'$ par la translation de vecteur $\overrightarrow{DA}$ sont aussi des points alignés.
Exercice 24
Écrivons le numéro de l'énoncé et la réponse choisie.
1) Si $ABCD$ est un parallélogramme alors :
b) $\overrightarrow{BC}= \overrightarrow{AD}$
2) Si le point $M$ est l'image de $B$ par la translation de vecteur $\overrightarrow{AB}$ alors :
c) $M$ est milieu de $[AM]$
3) Si $F$ est milieu de $[EG]$ alors :
b) $\overrightarrow{EF}=\overrightarrow{FG}$
Exercice 25
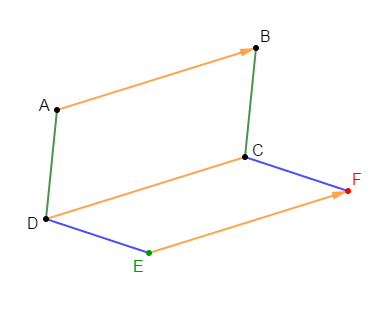
Soit $ABCD$ un parallélogramme et $E$ un point du plan.
1) Construisons le point $F$ tel que $\overrightarrow{EF}=\overrightarrow{AB}$
2) Démontrons que $EFCD$ est un parallélogramme.
En effet, on sait que $ABCD$ est un parallélogramme.
Ce qui entraine : $\overrightarrow{DC}=\overrightarrow{AB}$
Or, on a aussi : $\overrightarrow{EF}=\overrightarrow{AB}$
Par conséquent, $\overrightarrow{EF}=\overrightarrow{DC}$
D'où, $EFCD$ est un parallélogramme.

Exercice 26
1) Traçons un triangle $ABC.$
2) Construisons le point $F$ tel que $BCFA$ soit un parallélogramme.
3) Construisons le point $H$ de façon que $A$ soit le milieu de $[HB].$
4) Démontrons que $AHFC$ est un parallélogramme.
Comme $BCFA$ est un parallélogramme alors, on a : $\overrightarrow{FC}=\overrightarrow{AB}$
Or, on sait que $A$ est le milieu de $[HB].$ Ce qui signifie que : $\overrightarrow{HA}=\overrightarrow{AB}$
Ainsi, on obtient : $\overrightarrow{HA}=\overrightarrow{FC}$
Ce qui montre que $AHFC$ est un parallélogramme.

Exercice 27
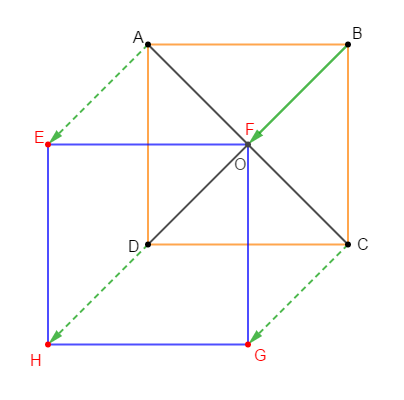
Soit un carré $ABCD$ de centre $O$ et de côté $4\;cm.$
Soit $t$ la translation de vecteur $\overrightarrow{BO}.$
1) Faisons la figure et construisons les points $E\;,\ F\;,\ G\ $ et $\ H$ images respectives des points $A\;,\ B\;,\ C\ $ et $\ D$ par $t.$
2) Démontrons que $EFGH$ est carré.
En effet, on a :
$$\left.\begin{array}{rcl} t_{\overrightarrow{BO}}(A)&=&E\\\\t_{\overrightarrow{BO}}(B)&=&F=O\\\\t_{\overrightarrow{BO}}(C)&=&G\\\\t_{\overrightarrow{BO}}(D)&=&H\\\\\end{array}\right\rbrace\ \Rightarrow\ t_{\overrightarrow{BO}}(ABCD)=(EFGH)$$
De plus, $ABCD$ est un carré.
Or, on sait que : l'image d'une figure géométrique par une translation de vecteur est une figure de même nature.
Par conséquent, $EFGH$ est un carré.

Exercice 28
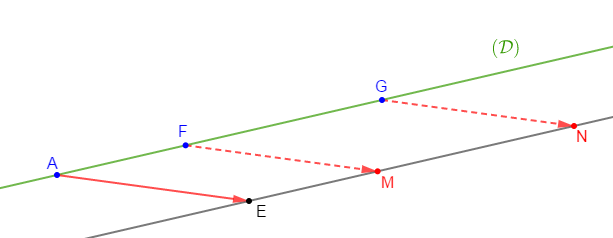
Soit $A\;,\ F\;,\ G$ trois points d'une droite $(\mathcal{D})\ $ et $\ E$ un point n'appartenant pas à $(\mathcal{D}).$
1) Construisons les points $M\ $ et $\ N$ images respectives des points $F\ $ et $\ G$ par la translation de vecteur $\overrightarrow{AE}.$
2) Démontrons que les points $E\;,\ M\ $ et $\ N$ sont alignés.
On a :
$$\left\lbrace\begin{array}{rcl} t_{\overrightarrow{AE}}(A)&=&E\\\\t_{\overrightarrow{AE}}(F)&=&M\\\\t_{\overrightarrow{AE}}(G)&=&N\end{array}\right.$$
Donc, $E\;,\ M\ $ et $\ N$ sont les images respectives des points $A\;,\ F\ $ et $\ G$ par la translation de vecteur $\overrightarrow{AE}.$
De plus, les points $A\;,\ F\ $ et $\ G$ sont alignés car ils appartiennent à la même droite $(\mathcal{D}).$
Or, on sait que : les images de points alignés par une translation de vecteur sont aussi des points alignés.
Par conséquent, les points $E\;,\ M\ $ et $\ N$ sont alignés.

Exercice 29
Soit $ABC$ est un triangle rectangle en $A.\ E\ $ et $\ F$ deux points distincts.
1) Construisons l'image $A'B'C'$ du triangle $ABC$ par la translation de vecteur $\overrightarrow{EF}$
2) $A'B'C'$ est un triangle rectangle en $A'$
En effet, $ABC$ est un triangle rectangle en $A\ $ et $\ A'B'C'$ son image par la translation de vecteur $\overrightarrow{EF}.$
Or, on sait que : l'image d'une figure géométrique par une translation de vecteur est une figure de même nature.
Par conséquent, $A'B'C'$ est un triangle rectangle en $A'.$

Auteur:
Diny Faye

Ajouter un commentaire