Solutions Serie d'exercices : Système d'équation et inéquation du 1er degré à deux inconnues - 2nd L
Exercice 1 : Méthode de substitution
Système \( S_1 \)
\[
\left\lbrace\begin{array}{rcl}
x - y + 7 &=& 0 \\
3x + y - 7 &=& 0
\end{array}\right.
\]
1. Isoler \( y \) dans la première équation :
\[
x - y + 7 = 0 \implies y = x + 7
\]
2. Substituer \( y \) dans la deuxième équation :
\[
3x + (x + 7) - 7 = 0 \implies 4x = 0 \implies x = 0
\]
3. Trouver \( y \) :
\[
y = 0 + 7 = 7
\]
Solution : \( (x, y) = (0, 7) \)
Système \( S_2 \)
\[
\left\lbrace\begin{array}{rcl}
x - y - 2 &=& 0 \\
2x + y + 5 &=& 0
\end{array}\right.
\]
1. Isoler \( y \) dans la première équation :
\[
x - y - 2 = 0 \implies y = x - 2
\]
2. Substituer \( y \) dans la deuxième équation :
\[
2x + (x - 2) + 5 = 0 \implies 3x + 3 = 0 \implies x = -1
\]
3. Trouver \( y \) :
\[
y = -1 - 2 = -3
\]
Solution : \( (x, y) = (-1, -3) \)
Système \( S_3 \)
\[
\left\lbrace\begin{array}{rcl}
2x + 5y - 16 &=& 0 \\
3x + 3y - 15 &=& 0
\end{array}\right.
\]
1. Simplifier la deuxième équation :
\[
3x + 3y - 15 = 0 \implies x + y = 5 \implies y = 5 - x
\]
2. Substituer \( y \) dans la première équation :
\[
2x + 5(5 - x) - 16 = 0 \implies 2x + 25 - 5x - 16 = 0 \implies -3x + 9 = 0 \implies x = 3
\]
3. Trouver \( y \) :
\[
y = 5 - 3 = 2
\]
Solution : \( (x, y) = (3, 2) \)
Système \( S_4 \)
\[
\left\lbrace\begin{array}{rcl}
-\dfrac{1}{3}x + y - 1 &=& 0 \\
2x - \dfrac{1}{4}y + 7 &=& 0
\end{array}\right.
\]
1. Isoler \( y \) dans la première équation :
\[
-\dfrac{1}{3}x + y - 1 = 0 \implies y = \dfrac{1}{3}x + 1
\]
2. Substituer \( y \) dans la deuxième équation :
\[
2x - \dfrac{1}{4}\left(\dfrac{1}{3}x + 1\right) + 7 = 0 \implies 2x - \dfrac{1}{12}x - \dfrac{1}{4} + 7 = 0
\]
\[
\dfrac{24}{12}x - \dfrac{1}{12}x = \dfrac{1}{4} - 7 \implies \dfrac{23}{12}x = -\dfrac{27}{4} \implies x = -\dfrac{27}{4} \times \dfrac{12}{23} = -\dfrac{81}{23}
\]
3. Trouver \( y \) :
\[
y = \dfrac{1}{3} \times \left(-\dfrac{81}{23}\right) + 1 = -\dfrac{27}{23} + \dfrac{23}{23} = -\dfrac{4}{23}
\]
Solution : \( (x, y) = \left(-\dfrac{81}{23}, -\dfrac{4}{23}\right) \)
Exercice 2 : Méthode d'addition
Partie a.
\[
\left\lbrace\begin{array}{rcl}
x + 3y &=& 1 \\
2x + y &=& 4
\end{array}\right.
\]
1. Multiplier la première équation par 2 :
\[
2x + 6y = 2
\]
2. Soustraire la deuxième équation :
\[
(2x + 6y) - (2x + y) = 2 - 4 \implies 5y = -2 \implies y = -\dfrac{2}{5}
\]
3. Trouver \( x \) :
\[
x + 3\left(-\dfrac{2}{5}\right) = 1 \implies x = 1 + \dfrac{6}{5} = \dfrac{11}{5}
\]
Solution : \( (x, y) = \left(\dfrac{11}{5}, -\dfrac{2}{5}\right) \)
Partie b.
\[
\left\lbrace\begin{array}{rcl}
2x + 3y - 1 &=& 0 \\
-3x + 2y + 5 &=& 0
\end{array}\right.
\]
1. Réécrire le système :
\[
\left\lbrace\begin{array}{rcl}
2x + 3y &=& 1 \\
-3x + 2y &=& -5
\end{array}\right.
\]
2. Multiplier la première équation par 3 et la deuxième par 2 :
\[
6x + 9y = 3 \\
-6x + 4y = -10
\]
3. Additionner les deux équations :
\[
13y = -7 \implies y = -\dfrac{7}{13}
\]
4. Trouver \( x \) :
\[
2x + 3\left(-\dfrac{7}{13}\right) = 1 \implies 2x = 1 + \dfrac{21}{13} = \dfrac{34}{13} \implies x = \dfrac{17}{13}
\]
Solution : \( (x, y) = \left(\dfrac{17}{13}, -\dfrac{7}{13}\right) \)
Partie c.
\[
\left\lbrace\begin{array}{rcl}
3x + 10y &=& 58 \\
10x + 3y &=& 72
\end{array}\right.
\]
1. Multiplier la première équation par 10 et la deuxième par 3 :
\[
30x + 100y = 580 \\
30x + 9y = 216
\]
2. Soustraire la deuxième équation de la première :
\[
91y = 364 \implies y = 4
\]
3. Trouver \( x \) :
\[
3x + 10(4) = 58 \implies 3x = 18 \implies x = 6
\]
Solution : \( (x, y) = (6, 4) \)
Partie d.
\[
\left\lbrace\begin{array}{rcl}
\dfrac{1}{3}x - \dfrac{1}{2}y &=& 1 \\
-x + \dfrac{2}{3}y &=& \dfrac{2}{3}
\end{array}\right.
\]
1. Éliminer les fractions en multipliant par 6 et 3 respectivement :
\[
2x - 3y = 6 \\
-3x + 2y = 2
\]
2. Multiplier la première équation par 3 et la deuxième par 2 :
\[
6x - 9y = 18 \\
-6x + 4y = 4
\]
3. Additionner les deux équations :
\[
-5y = 22 \implies y = -\dfrac{22}{5}
\]
4. Trouver \( x \) :
\[
2x - 3\left(-\dfrac{22}{5}\right) = 6 \implies 2x = 6 - \dfrac{66}{5} = -\dfrac{36}{5} \implies x = -\dfrac{18}{5}
\]
Solution : \( (x, y) = \left(-\dfrac{18}{5}, -\dfrac{22}{5}\right) \)
Exercice 3 : Méthode graphique
Système \( S_1 \)
\[
\left\lbrace\begin{array}{rcl}
x - y + 3 &=& 0 \\
2x - y + 2 &=& 0
\end{array}\right.
\]
1. Trouver les points d'intersection :
Pour la première équation \(x - y + 3 = 0\)
- Pour \( x = 0 \), \( y = 3 \) ).
- Pour \( y = 0 \), \( x = -3 \)).
Pour la deuxième équation \2x - y + 2 = 0\
- Pour \( x = 0 \), \( y = 2 \).
- Pour \( y = 0 \), \( x = -1 \).
2. Construction graphique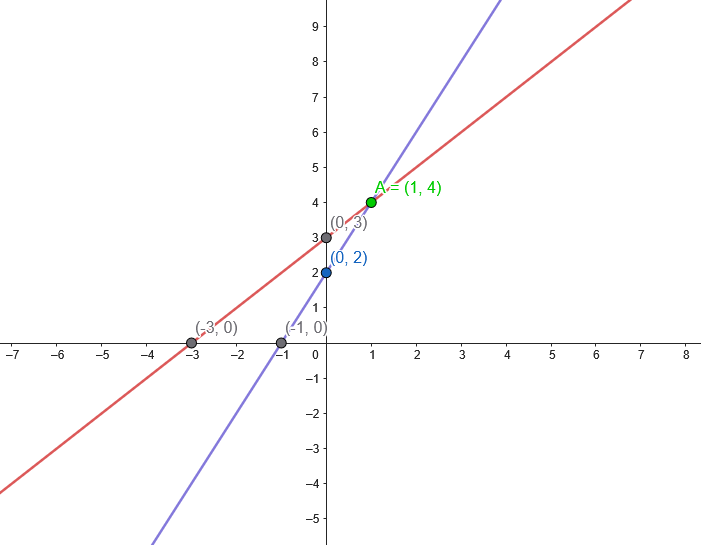
3. Solution graphique : Les droites se coupent en \( (1, 4) \).
Solution : \( (x, y) = (1, 4) \)
Système \( S_2 \)
\[
\left\lbrace\begin{array}{rcl}
2x - y - 4 &=& 0 \\
2x - y + 2 &=& 0
\end{array}\right.
\]
- Analyse : Les deux équations représentent des droites parallèles (même coefficient directeur).
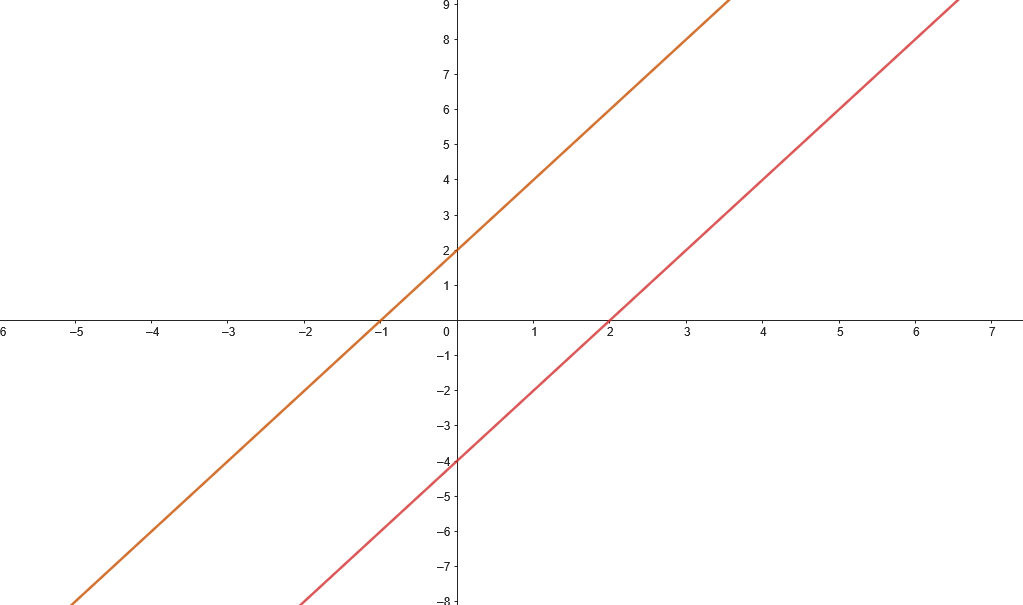
Solution : Aucune solution (système incompatible).
Système \( S_3 \)
\[
\left\lbrace\begin{array}{rcl}
x - y + 3 &=& 0 \\
2x - 2y + 6 &=& 0
\end{array}\right.
\]
- Analyse : La deuxième équation est un multiple de la première.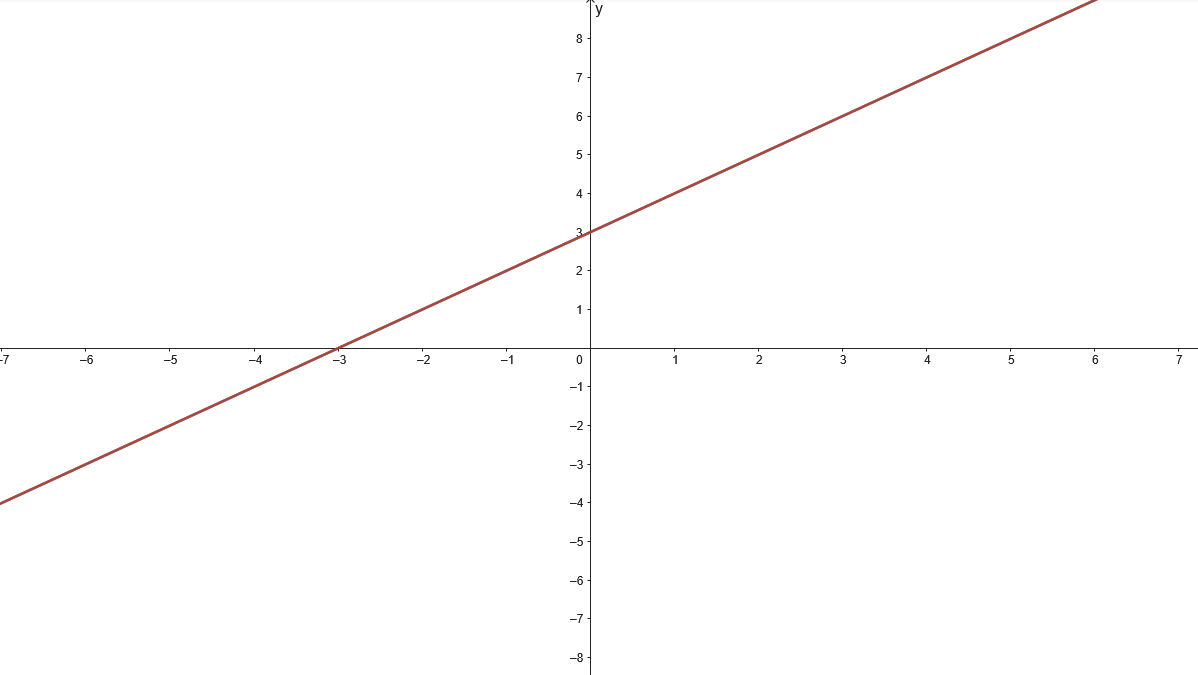
Solution : Infinité de solutions (droites confondues).
Système \( S_4 \)
\[
\left\lbrace\begin{array}{rcl}
x - y - 1 &=& 0 \\
2x - y + 2 &=& 0 \\
-x + 3y + 9 &=& 0
\end{array}\right.
\]
1. Résoudre les deux premières équations :
\[
\left\lbrace\begin{array}{rcl}
x - y &=& 1 \\
2x - y &=& -2
\end{array}\right. \implies x = -3, y = -4
\]
2. Vérifier dans la troisième équation :
\[
-(-3) + 3(-4) + 9 = 3 - 12 + 9 = 0 \quad \text{(vérifié)}
\]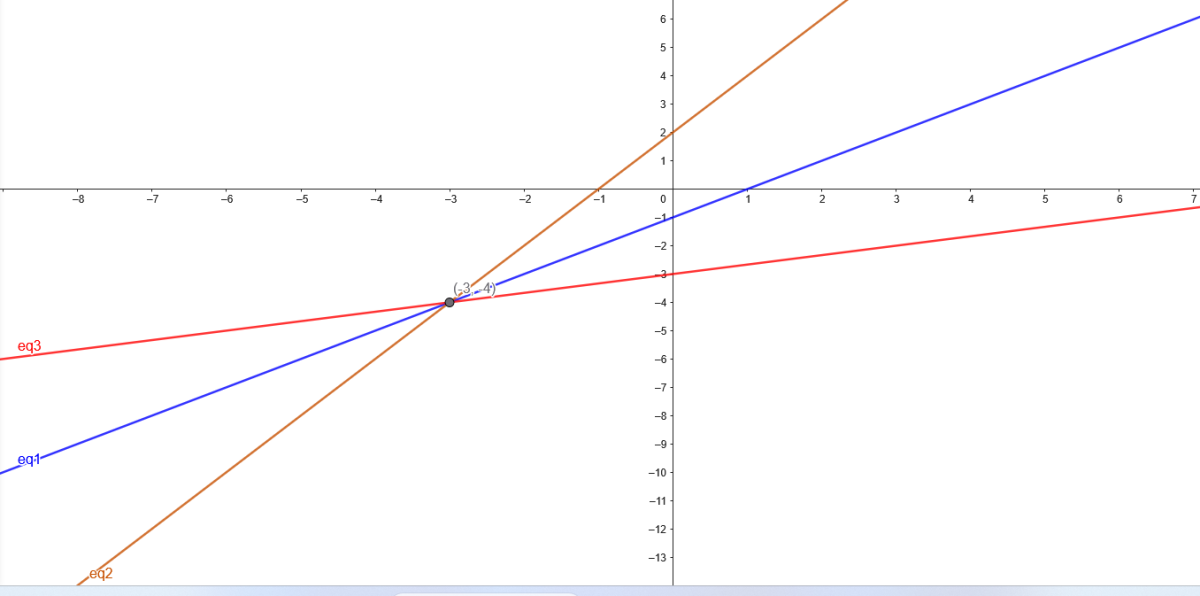
Solution : \( (x, y) = (-3, -4) \)
Exercice 4 : Problème avec systèmes d'équations
Partie 1
\[
\left\lbrace\begin{array}{rcl}
x + 2y &=& 625 \\
6x + 13y &=& 3975
\end{array}\right.
\]
1. Multiplier la première équation par 6 :
\[
6x + 12y = 3750
\]
2. Soustraire la deuxième équation :
\[
y = 225
\]
3. Trouver \( x \) :
\[
x + 2(225) = 625 \implies x = 175
\]
Solution : \( (x, y) = (175, 225) \)
Partie 2
- Avant dévaluation :
- Prix pommes de terre : \( x = 175 \, \text{F/kg} \)
- Prix oignons : \( y = 225 \, \text{F/kg} \)
- Après dévaluation :
- Pommes de terre : \( 1.2 \times 175 = 210 \, \text{F/kg} \)
- Oignons : \( 1.3 \times 225 = 292.5 \, \text{F/kg} \)
Vérification :
\[
10 \times 210 + 20 \times 292.5 = 2100 + 5850 = 7950 \, \text{F} \quad \text{(correct)}
\]
Exercice 5 : Résolution graphique d'inéquations
Partie a.
\[
\left\lbrace\begin{array}{rcl}
x + y - 1 &\geq& 0 \\
2x - y + 4 &<& 0
\end{array}\right.
\]
- Représentation graphique :
\( x + y \geq 1 \) : Zone au-dessus de la droite \( y = -x + 1 \).
\( 2x - y < -4 \) : Zone en dessous de la droite \( y = 2x + 4 \).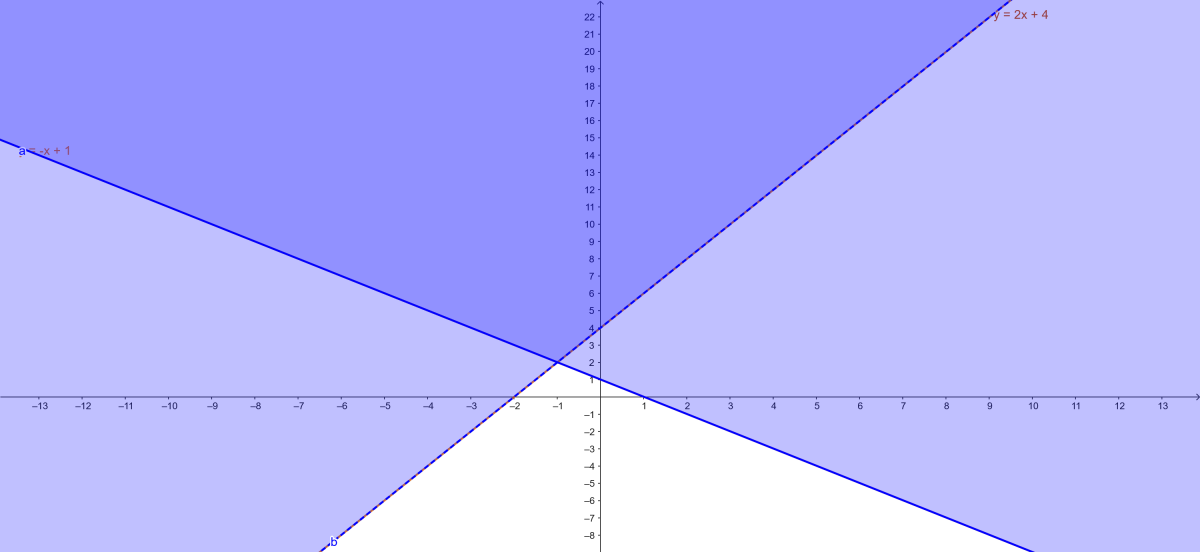
Solution : Intersection des deux zones.
Partie b.
\[
\left\lbrace\begin{array}{rcl}
2x + y - 1 &\geq& 0 \\
-2x + y + 2 &<& 0
\end{array}\right.
\]
- Représentation graphique :
- \( 2x + y \geq 1 \) : Zone au-dessus de la droite \( y = -2x + 1 \).
- \( -2x + y < -2 \) : Zone en dessous de la droite \( y = 2x - 2 \).
Solution : Intersection des deux zones.
### Système c :
\[
\left\lbrace\begin{array}{rcl}
3x - 2y - 1 & < & 0 \\
x + 2y + 3 & \geq & 0 \\
x + y & > & 0
\end{array}\right.
\]
Étape 1 : Tracer les droites correspondantes
1. Première inéquation : \( 3x - 2y - 1 < 0 \)
Droite associée : \( 3x - 2y - 1 = 0 \)
Points pour tracer :
- Si \( x = 0 \), \( -2y - 1 = 0 \Rightarrow y = -0.5 \) → $A (0, -0.5)$
- Si \( y = 0 \), \( 3x - 1 = 0 \Rightarrow x = \frac{1}{3} \) → $B(1/3, 0$)
Inégalité stricte : la droite est en pointillés.
Test du point (0,0) : \( 0 - 0 - 1 < 0 \) → Vrai. Donc, on prend le côté contenant (0,0).
2. Deuxième inéquation : \( x + 2y + 3 \geq 0 \)
Droite associée : \( x + 2y + 3 = 0 \)
Points pour tracer :
- Si \( x = 0 \), \( 2y + 3 = 0 \Rightarrow y = -1.5 \) →$C(0, -1.5)$
- Si \( y = 0 \), \( x + 3 = 0 \Rightarrow x = -3 \) → $D(-3, 0)$
Inégalité large : la droite est continue.
Test du point (0,0) : \( 0 + 0 + 3 \geq 0 \) → Vrai. Donc, on prend le côté contenant (0,0).
3. Troisième inéquation : \( x + y > 0 \)
Droite associée : \( x + y = 0 \)
Points pour tracer :
- $0(0,0)$ et $E(1,-1)$
Inégalité stricte : la droite est en pointillés.
Test du point (1,0) : \( 1 + 0 > 0 \) → Vrai. Donc, on prend le côté contenant (1,0).
Étape 2 : Trouver l'intersection des régions
La solution est l'intersection des trois régions définies ci-dessus. Graphiquement, cela correspond à la zone où toutes les inégalités sont satisfaites simultanément.
Points d'intersection des droites :
1. Intersection de \( 3x - 2y = 1 \) et \( x + 2y = -3 \) :
Addition : \( 4x = -2 \Rightarrow x = -0.5 \)
\( -0.5 + 2y = -3 \Rightarrow 2y = -2.5 \Rightarrow y = -1.25 \) → (-0.5, -1.25)
2. Intersection de \( 3x - 2y = 1 \) et \( x + y = 0 \) :
\( y = -x \)
\( 3x - 2(-x) = 1 \Rightarrow 5x = 1 \Rightarrow x = 0.2 \)
\( y = -0.2 \) → (0.2, -0.2)
3. Intersection de \( x + 2y = -3 \) et \( x + y = 0 \) :
\( y = -x \)
\( x + 2(-x) = -3 \Rightarrow -x = -3 \Rightarrow x = 3 \)
\( y = -3 \) → (3, -3)
La région solution est un triangle délimité par ces points, mais en vérifiant les inégalités, la zone valide est celle où \( x + y > 0 \) domine, donc la partie supérieure.
Solution graphique :** La région est l'intersection des trois demi-plans, qui forme un polygone infini vers le haut à gauche.
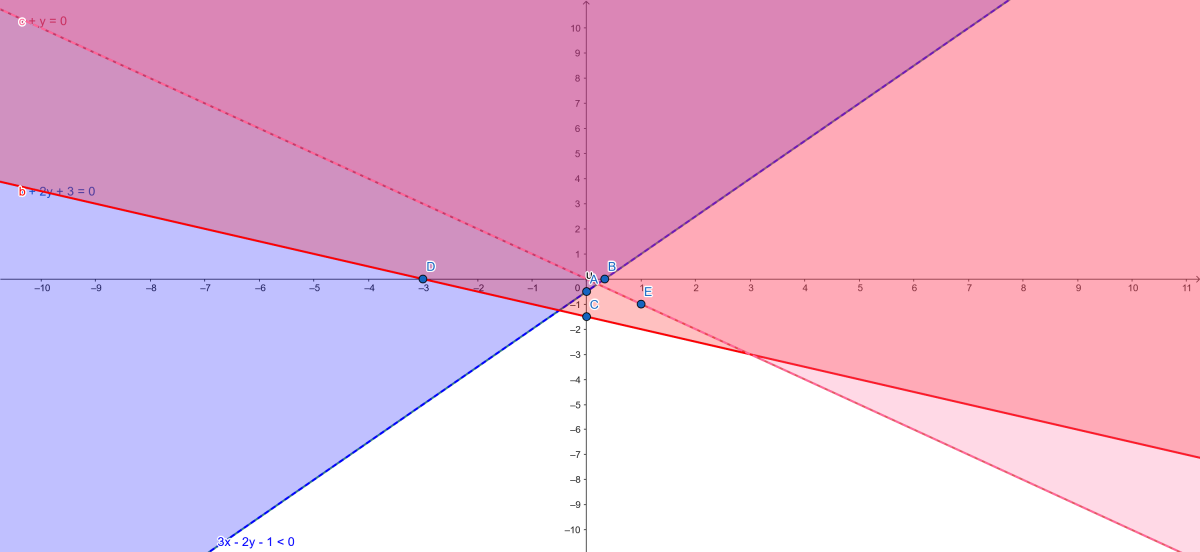
Système d :
\[
\left\lbrace\begin{array}{rcl}
3x - 2y + 5 & \geq & 0 \\
2x + y - 2 & \leq & 0 \\
x - 2 & \geq & 0
\end{array}\right.
\]
Étape 1 : Tracer les droites correspondantes
1. Première inéquation : \( 3x - 2y + 5 \geq 0 \)
Droite associée : \( 3x - 2y + 5 = 0 \)
Points :
- \( x = 0 \), \( -2y + 5 = 0 \Rightarrow y = 2.5 \) →$A (0, 2.5)$
- \( y = 0 \), \( 3x + 5 = 0 \Rightarrow x = -\frac{5}{3} \) → $B(-5/3, 0)$
Inégalité large : droite continue.
Test (0,0) : \( 0 - 0 + 5 \geq 0 \) → Vrai. prend côté (0,0).
2. Deuxième inéquation : \( 2x + y - 2 \leq 0 \)
Droite associée : \( 2x + y - 2 = 0 \)
Points :
- \( x = 0 \), \( y = 2 \) → $C(0, 2)$
- \( y = 0 \), \( 2x = 2 \Rightarrow x = 1 \) → $D(1, 0)$
Inégalité large : droite continue.
Test (0,0) : \( 0 + 0 - 2 \leq 0 \) → Vrai. prend côté (0,0).
3. Troisième inéquation : \( x - 2 \geq 0 \)
Droite associée : \( x = 2 \) (verticale)
Inégalité large : droite continue.
prend à droite de \( x = 2 \).
Étape 2 : Intersection des régions
La solution doit satisfaire les trois inégalités simultanément.
Points d'intersection :
1. Intersection de \( 3x - 2y = -5 \) et \( 2x + y = 2 \) :
Résoudre \( y = 2 - 2x \)
\( 3x - 2(2 - 2x) = -5 \Rightarrow 3x - 4 + 4x = -5 \Rightarrow 7x = -1 \Rightarrow x = -\frac{1}{7} \)
\( y = 2 - 2(-\frac{1}{7}) = \frac{16}{7} \) →$E (-1/7, 16/7)$
2. Intersection de \( 3x - 2y = -5 \) et \( x = 2 \) :
\( 6 - 2y = -5 \Rightarrow -2y = -11 \Rightarrow y = 5.5 \) → $F(2, 5.5)$
3. Intersection de \( 2x + y = 2 \) et \( x = 2 \) :
\( 4 + y = 2 \Rightarrow y = -2 \) →$G (2, -2)$
La région solution est la partie où \( x \geq 2 \), en dessous de \( 2x + y \leq 2 \) et au-dessus de \( 3x - 2y \geq -5 \). Cela forme un triangle entre (2, -2), (2, 5.5), et l'intersection à l'infini.
Solution graphique : Un secteur angulaire partant de (2, -2) hachuré..
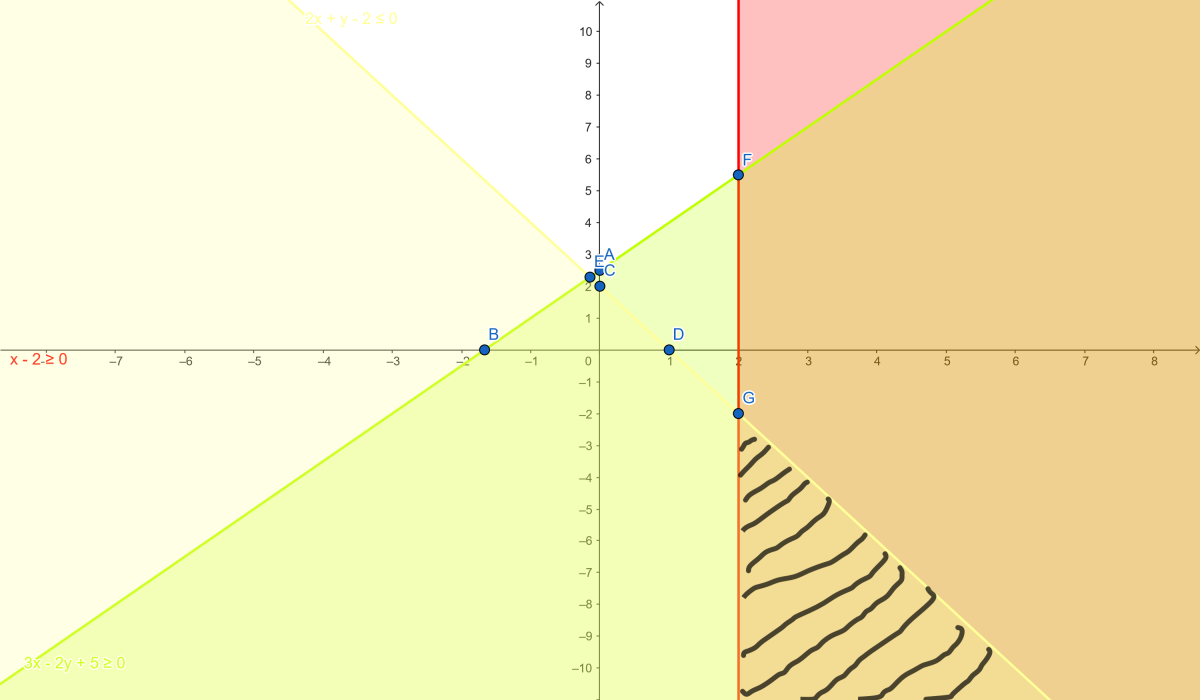
Système f :
\[
\left\lbrace\begin{array}{rcl}
x - y + 2 & \leq & 0 \\
2x + y + 1 & < & 0 \\
y - 1 & < & 0
\end{array}\right.
\]
Étape 1 : Tracer les droites correspondantes
1. Première inéquation : \( x - y + 2 \leq 0 \)
Droite associée : \( x - y + 2 = 0 \)
Points :
- \( x = 0 \), \( -y + 2 = 0 \Rightarrow y = 2 \) → $A(0, 2)$
- \( y = 0 \), \( x + 2 = 0 \Rightarrow x = -2 \) → $B(-2, 0)$
Inégalité large : droite continue.
Test (0,0) : \( 0 - 0 + 2 \leq 0 \) → Faux. prend le côté opposé à (0,0).
2. Deuxième inéquation : \( 2x + y + 1 < 0 \)
Droite associée : \( 2x + y + 1 = 0 \)
Points :
- \( x = 0 \), \( y = -1 \) → $C(0, -1) $
- \( y = 0 \), \( 2x + 1 = 0 \Rightarrow x = -0.5 \) → $D(-0.5, 0)$
Inégalité stricte : droite en pointillés.
Test (0,0) : \( 0 + 0 + 1 < 0 \) → Faux. prend le côté opposé à (0,0).
3. Troisième inéquation : \( y - 1 < 0 \)
Droite associée : \( y = 1 \) (horizontale)
Inégalité stricte : droite en pointillés.
prend en dessous de \( y = 1 \).
Étape 2 : Intersection des régions
La solution est l'intersection des trois régions.
Points d'intersection :
1. Intersection de \( x - y = -2 \) et \( 2x + y = -1 \) :
Addition : \( 3x = -3 \Rightarrow x = -1 \)
\( -1 - y = -2 \Rightarrow y = 1 \) → $E(-1, 1)$
2. Intersection de \( x - y = -2 \) et \( y = 1 \) :
\( x - 1 = -2 \Rightarrow x = -1 \) → (-1, 1) (même point)
3. Intersection de \( 2x + y = -1 \) et \( y = 1 \) :
\( 2x + 1 = -1 \Rightarrow 2x = -2 \Rightarrow x = -1 \) → (-1, 1)
La région solution est la zone où \( y < 1 \), en dessous de \( x - y \leq -2 \) et \( 2x + y < -1 \). Cela forme un secteur angulaire partant deF (-1,1) vers le bas à gauche(Secteur Angulaire bleu foncé.
Solution graphique : Un secteur infini vers le bas à gauche à partir de (-1,1).
Résumé des solutions graphiques :
- c. La solution est la région où toutes les inégalités sont satisfaites, formant un polygone.
- d. La solution est la région à droite de \( x = 2 \), en dessous de \( 2x + y \leq 2 \) et au-dessus de \( 3x - 2y \geq -5 \).
- f. La solution est la région en dessous de \( y = 1 \), en dessous de \( x - y \leq -2 \) et \( 2x + y < -1 \).
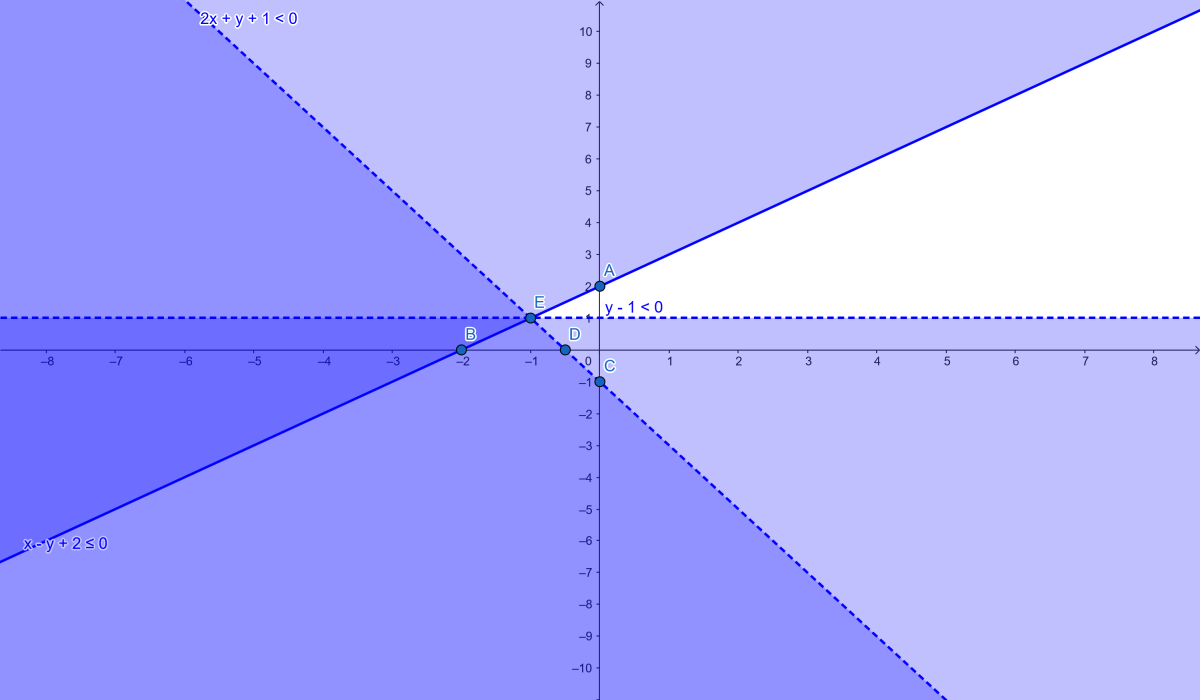
Exercice 6 : Problème de mélange
Contraintes :
\[
\left\lbrace\begin{array}{rcl}
x + y &\geq& 10 \\
600x + 400y &\leq& 6000 \\
x, y &\geq& 0
\end{array}\right.
\]
1. Simplifier la deuxième inéquation :
\[
3x + 2y \leq 30
\]
2. Représentation graphique :
- Zone réalisable délimitée par \( x + y \geq 10 \), \( 3x + 2y \leq 30 \), et \( x, y \geq 0 \).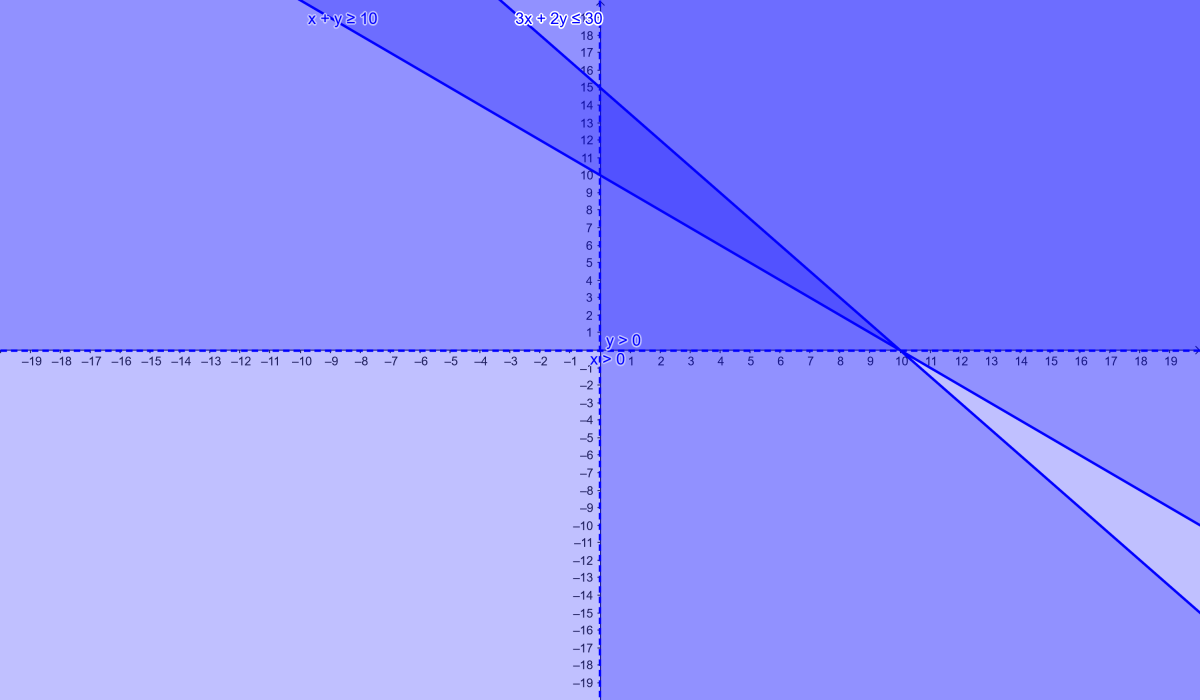
Solution : Tous les couples \( (x, y) \) dans la zone réalisable.
Résolution 2
Problème de Karine : Optimisation du cocktail de jus de fruits
Données :
- Jus de goyave :
- Prix par litre : \(600\,F\)
- Quantité achetée : \(x\) litres
- Jus d'ananas :
- Prix par litre : \(400\,F\)
- Quantité achetée : \(y\) litres
- Contraintes :
1. Volume total : Au moins \(10\) litres de cocktail.
\[
x + y \geq 10
\]
2. Budget : Ne dépasse pas \(6000\,F\).
\[
600x + 400y \leq 6000
\]
3. Quantités positives :
\[
x \geq 0, \quad y \geq 0
\]
Étape 1 : Simplification des inéquations
1. Contrainte budgétaire :
\[
600x + 400y \leq 6000 \quad \Rightarrow \quad 3x + 2y \leq 30 \quad (\text{divisé par } 200)
\]
2. Contrainte de volume :
\[
x + y \geq 10
\]
Étape 2 : Tracé des droites correspondantes
1. Droite budgétaire : \(3x + 2y = 30\)
- Si \(x = 0\), \(y = 15\) → \((0, 15)\)
- Si \(y = 0\), \(x = 10\) → \((10, 0)\)
- Inégalité : \(3x + 2y \leq 30\) → en dessous de la droite.
2. Droite de volume : \(x + y = 10\)
- Si \(x = 0\), \(y = 10\) → \((0, 10)\)
- Si \(y = 0\), \(x = 10\) → \((10, 0)\)
- Inégalité : \(x + y \geq 10\) → au-dessus de la droite.
3. Contraintes de positivité :
- \(x \geq 0\) → à droite de l'axe \(y\).
- \(y \geq 0\) → au-dessus de l'axe \(x\).
Étape 3 : Intersection des régions
Zone réalisable :
- Intersection de :
- \(x + y \geq 10\) (au-dessus de la droite verte),
- \(3x + 2y \leq 30\) (en dessous de la droite bleue),
- \(x \geq 0, y \geq 0\) (premier quadrant).
Points d'intersection :
1. Intersection de \(x + y = 10\) et \(3x + 2y = 30\) :
\[
\begin{cases}
x + y = 10 \\
3x + 2y = 30
\end{cases}
\]
- De \(x + y = 10\), on a \(y = 10 - x\).
- Substitution : \(3x + 2(10 - x) = 30\)
\(\Rightarrow 3x + 20 - 2x = 30\)
\(\Rightarrow x = 10\)
\(\Rightarrow y = 0\)
→ Point : \((10, 0)\)
2. Intersection de \(3x + 2y = 30\) avec \(y = 0\) :
- \(3x = 30 \Rightarrow x = 10\)
→ Point : \((10, 0)\) (identique au précédent).
3. Intersection de \(x + y = 10\) avec \(x = 0\) :
- \(y = 10\)
→ Point : \((0, 10)\)
4. Vérification de \((0, 10)\) dans \(3x + 2y \leq 30\) :
- \(0 + 20 = 20 \leq 30\) → Valide.
Étape 4 : Solution graphique
La zone réalisable est un polygone délimité par les points :
- \((0, 10)\) → Maximum de jus d'ananas,
- \((10, 0)\) → Maximum de jus de goyave,
- Tous les points sur le segment entre \((0, 10)\) et \((10, 0)\).
Interprétation :
- Karine peut acheter n'importe quelle combinaison \((x, y)\) telle que :
\[
x + y \geq 10 \quad \text{et} \quad 3x + 2y \leq 30
\]
avec \(x \geq 0, y \geq 0\).
Exemples de solutions possibles :
1. Que du jus d'ananas :
\(x = 0\), \(y = 10\) → Coût : \(0 \times 600 + 10 \times 400 = 4000\,F\) (sous le budget).
2. Que du jus de goyave :
\(x = 10\), \(y = 0\) → Coût : \(10 \times 600 + 0 \times 400 = 6000\,F\) (budget max).
3. Mélange équilibré :
\(x = 5\), \(y = 5\) →
Volume : \(5 + 5 = 10\) litres,
Coût : \(5 \times 600 + 5 \times 400 = 5000\,F\) (acceptable).
Conclusion :
Les valeurs possibles de \((x, y)\) sont tous les points du segment reliant \((0, 10)\) à \((10, 0)\) qui satisfont :
\[
\boxed{
\begin{cases}
x + y \geq 10 \\
3x + 2y \leq 30 \\
x \geq 0, y \geq 0
\end{cases}
}
\]
Représentation graphique :
- Axe \(x\) : Jus de goyave (litres),
- Axe \(y\) : Jus d'ananas (litres).
- Zone hachurée : Entre les droites \(x + y = 10\) et \(3x + 2y = 30\) dans le premier quadrant.
Solution optimale :
- Si Karine veut minimiser le coût, elle prendra plus de jus d'ananas (moins cher).
- Si elle veut maximiser le volume, elle peut aller jusqu'à \(10\) litres avec n'importe quelle combinaison sur la droite \(x + y = 10\).

Ajouter un commentaire