Vous êtes ici

Série d'exercices : Rotations et polygones réguliers 4e

Classe:

Quatrième

Exercice 1

1) Définir un angle au centre.

2) En utilisant la figure ci-dessous ; nommer les angles au centre.

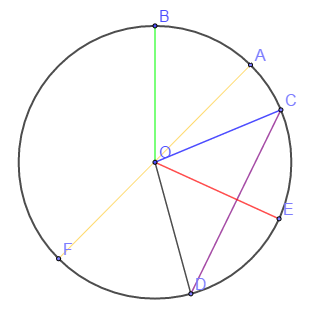
Exercice 2

Soit

$\mathcal{C}$ un cercle de centre

$O$ et de rayon

$3\;cm.\ \widehat{ENS}$ est un angle au centre. Compléter le tableau suivant : On donne

$\pi=3.$

$\begin{array}{|l|c|c|c|c|}\hline Mes\ \widehat{ENS}&30^{\circ}&\:\:\ &126^{\circ}& \\ \hline\text{Longueur de l'arc}& & & & \\ \text{intercepté par}& &\dfrac{2\pi}{3}& &\dfrac{\pi}{3} \\ \widehat{ENS}\text{ en }cm& & & & \\ \hline\end{array}$

Exercice 3

Soient

$[MN]$ et

$[M'N']$ deux segments de même longueur dont les supports ne sont pas parallèles.

1) Faire une figure.

2) Par une certaine rotation, l'image de

$M$ est

$M'$ et l'image de

$N$ est

$N'.$

3) Construire le centre

$O$ de cette rotation.

Exercice 4

$A$ et

$B$ sont deux points du plan tel que :

$AB=4\;cm$

1) Construire le point

$C$ image de

$B$ par la rotation de centre

$A$ et d'angle

$45^{\circ}$ dans le sens positif.

2) Construire le point

$D$ image

$B$ par la rotation de centre

$A$ et d'angle

$45^{\circ}$ dans le sens négatif.

3) Quelle est la nature du triangle

$CAD$ ? Justifier la réponse.

Exercice 5

Soit un triangle équilatérale

$ABC$ et la rotation de centre

$A$ et d'angle

$60^{\circ}.$

1) Construire l'image

$D$ de

$C$ et l'image

$E$ de

$D$ par cette rotation.

2) Montrer que

$BA=CD$ et

$AE=CD.$

3) Quelle est la nature du quadrilatère

$EBCD$ ? Justifier.

Exercice 6

Soit

$\mathcal{C}$ un cercle de centre

$O.\ A$ et

$B$ sont deux points de

$\mathcal{C}$ tels que la longueur de l'arc

$\overset{\displaystyle\frown}{AB}$ est de

$3,14.$ Cette longueur est égale à

$\dfrac{1}{8}$ du périmètre de

$\mathcal{C}.$

1) Calculer le rayon du cercle

$\mathcal{C}.$

2) Calculer la mesure de l'angle au centre.

Exercice 7

1) Soit

$\mathcal{C}$ est un cercle de centre

$O$ et de rayon

$4\;cm.$

2) Placer deux points

$A$ et

$B$ sur ce cercle tel que :

$mes \;AOB = 80^{\circ}.$

3) Calculer la longueur de l'arc

$\overset{\displaystyle\frown}{AB}\quad (\pi=3).$

Exercice 8

1) Construire un triangle équilatéral

$ABC$ inscrit dans un cercle

$(c)$ de centre

$O$ et de rayon

$4\;cm.$

2) Quelle est la longueur de chacun des arcs

$\overset{\displaystyle\frown}{AB}\;,\ \overset{\displaystyle\frown}{AC}$ et

$\overset{\displaystyle\frown}{BC}\ ?$

Exercice 9

1) Construire un pentagone régulier inscrit dans un cercle de rayon

$3,5\;cm.$

2) Déterminer trois rotations différentes qui laissent globalement invariant un triangle équilatéral.

Exercice 10

1) Trace le cercle

$(\mathcal{C})$ de centre

$O$ et de rayon

$4\;cm$ puis marque

$4$ points

$A$ ,

$B$ ,

$C$ et

$D$ du cercle.

2) Cite un angle au centre qui intercepte l'arc

$\overset{\displaystyle\frown}{AB}$

3) Cite deux angles au centre et l'arc intercepté par chacun d'eux.

Exercice 11

Soit

$(\mathcal{C})$ un cercle de centre

$O$ et de rayon

$R.$

$A$ et

$B$ deux points de

$(\mathcal{C}).$

Dans chacun des cas ci-dessous calcule la longueur de l'arc

$\overset{\displaystyle\frown}{AB}$

$R=3\;cm\;,\ \widehat{AOB}=60^{\circ}.$

$R=3\;cm\;,\ \widehat{AOB}=45^{\circ}.$

$R=4.5\;cm\;,\ \widehat{AOB}=90^{\circ}.$

Exercice 12

1) Construis un triangle

$ABC$ isocèle en

$A$ tel que

$\widehat{BAC}=50^{\circ}.$

2) Marque deux points

$E$ et

$F$ puis construis leurs images respectives

$E'$ ,

$F'$ par la rotation de centre

$A$ qui transforme

$B$ en

$C.$

Exercice 13

$ABCD$ est un losange de centre

$J$ tel que

$\widehat{DAB}=30^{\circ}.$

1) Fais une figure

2) Quelle est l'image de

$D$ par la rotation de centre

$A$ de sens celui des aiguilles d'une montre et d'angle

$30^{\circ}$ ?

Exercice 14

1) Trace le segment

$[AO]$ de longueur

$3\;cm.$

2) Construis le point

$M$ image de

$A$ dans la rotation de centre

$O$ et d'angle

$90^{\circ}.$ (sens direct).

3) Construis le point

$I$ , image de

$M$ dans la rotation dans le sens direct de centre

$O$ et d'angle

$\widehat{AOM}.$

4) Construis le point

$E$ image de

$I$ dans la même rotation.

5) Dans la rotation de centre

$O$ et d'angle

$90^{\circ}$ dans le sens contraire des aiguilles d'une montre, quelle est l'image du point

$I.$

6) Donne la nature du quadrilatère

$AMIE.$

Exercice 15

$I$ ,

$A$ ,

$B$ sont des points du plan.

Construis la figure ci-dessous par la rotation de centre

$I$ qui transforme

$A$ en

$B.$

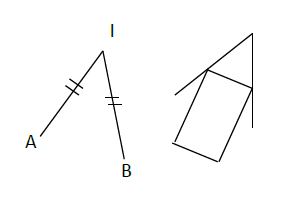
Exercice 16

$[Ox)$ ,

$[Oy)$ et

$[Oz)$ sont trois demi-droites.

$A$ un point situé sur

$[Ox)$ ,

$B$ et

$D$ sur

$[Oy)$ et

$C$ sur

$[Oz)$ , avec

$OC=OD=5\;cm$ et

$OA=OB=4\;cm$ ;

$\widehat{xOz}=\widehat{zOy}=40^{\circ}.$

1) Fais une figure.

2) Démontre que

$AD=BC$ en utilisant une rotation à préciser.

Exercice 17

Soit

$ABCD$ est un carré de centre

$I$ ,

$M$ et

$N$ les milieux respectifs de

$[AB]$ et

$[AD].$

1) Fais une figure.

2) Justifie que

$M$ est l'image de

$N$ dans la rotation de centre

$I$ qui transforme

$A$ en

$B.$

3) Justifie que

$ONM$ est un triangle isocèle.

4) Compare en justifiant :

$CN$ et

$DM.$

$\widehat{AIN}$ et

$\widehat{BIN}.$

c) Les aires des triangles

$BDM$ et

$CAN.$

d) Les aires des triangles

$AIN$ et

$BIM.$

5) Détermine l'aire du quadrilatère

$AMIN.$

Exercice 18

Reproduis le triangle

$ABC$ ci-dessous.

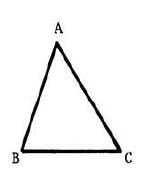
1) Construis extérieurement à ce triangle

2) les carrés

$ABDE$ et

$ACFG.$

3) Démontre que

$EC=BG$ et que

$(EC)$ est perpendiculaire à

$(BG).$

4) Démontrer que les droites

$(EC)$ et

$(DB)$ sont perpendiculaires.

5) Comparer les distances

$EC$ et

$DB.$

Exercice 19

Le quadrilatère

$A'B'C'D'$ est l'image de

$ABCD$ par la rotation de centre

$O$ et d'angle

$60^{\circ}.$

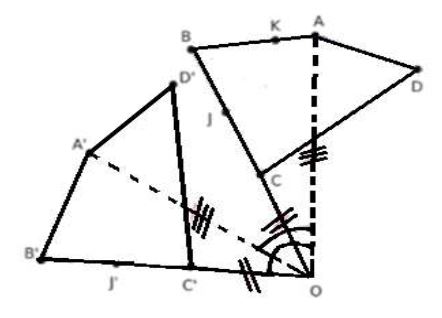
1) Compare en justifiant les aires et les périmètres de ces deux quadrilatères

2) Le point

$J$ est le milieu du segment

$[BC]$ , son image

$J'$ par cette rotation est-elle le milieu du segment

$[B'C']$ ?

Justifie ta réponse.

3) L'angle

$\widehat{A'B'C'}$ étant l'image de l'angle

$\widehat{ABC}$ par cette rotation, compare leurs mesures.

Justifie ta réponse.

Exercice 20

Construis un triangle

$AOB$ isocèle en

$O$ tel que

$\widehat{AOB}=45^{\circ}.$

Dans la rotation de centre

$O$ et d'angle

$\widehat{AOB}$ dans le sens contraire des aiguilles d'une montre, construis :

1) Le point

$C$ image de

$B$ ,

2) Le point

$D$ image de

$C$ ,

3) Le point

$E$ image de

$D$ ,

4) Le point

$F$ image de

$E.$

5) Quelle est l'image du point

$F.$

6) Précise la nature du polygone

$ABCDEF.$

Exercice 21

1) Construis un carré

$CABE$ de centre

$I.$

2) Par la rotation de centre

$I$ et d'angle

$45^{\circ}$ dans le sens direct, construis

$M$ ,

$N$ ,

$R$ et

$S$ images respectives des points

$C$ ,

$A$ ,

$B$ , et

$E.$

3) Trace le polygone

$CMANBRES$ puis donne sa nature ?

4) Indique le centre et le rayon du cercle circonscrit au polygone

$CMANBRES.$

5) Trace ce cercle circonscrit à ce polygone.

Exercice 22

$ABC$ est un triangle équilatéral de côté

$3\;cm.$

Le cercle

$(\mathcal{C})$ circonscrit au triangle a pour centre

$I.$

Par la rotation de centre

$I$ et d'angle

$60^{\circ}$ dans le sens contraire des aiguilles d'une montre,

$A$ a pour image

$D$ ,

$B$ a pour image

$E$ et

$C$ a pour image

$F.$

1) Construis le triangle

$ABC$ puis trace le cercle

$(\mathcal{C}).$

2) Justifie que les points

$D$ ,

$E$ et

$F$ appartiennent au cercle.

3) Donne la nature du polygone

$ADBECF.$

4) Indique le centre et le rayon du cercle inscrit au polygone

$ADBECF.$

Exercice 23

1) Construis un triangle

$IEF$ isocèle en

$I$ dont les angles à la base mesurent

$75^{\circ}.$

2) Dans la rotation de sens indirect de centre

$I$ qui transforme

$E$ en

$F$ , construis le point

$G$ image de

$F$ , le point

$H$ image de

$G$ , le point

$R$ image de

$H.$

3) Quelle est l'image de

$R$ ?

Précise la nature du polygone

$EFGHR.$

4) Explique comment obtenir le cercle inscrit à ce polygone.

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$

Auteur:

Diny Faye & adem

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Série d'exercices : Rotations et polygones réguliers 4e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Exercice 21

Exercice 22

Exercice 23

▸Correction des exercices\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}

Ajouter un commentaire

Plain text

$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$