Corrigé Bac Maths S2 S4 S5 1er groupe 2018

 

1) a) Si $x<-1\text{ alors }F(x)=0$;

 

$$\begin{eqnarray} lim_{x\rightarrow -\infty}F(x)& =& \lim_{x\rightarrow -\infty}0\nonumber\\ &=& 0.\nonumber \end{eqnarray}$$

 

Si $x\geq 3\text{ alors }F(x)=1$;

 

$$\begin{eqnarray} lim_{x\rightarrow +\infty}F(x)& =& \lim_{x\rightarrow +\infty}1\nonumber\\ &=& 1.\nonumber \end{eqnarray}$$

 

b) Soit $U$ l'ensemble des valeurs possibles de $X$

 

$U={-1\;;\ 0\;;\ 1\;;\ 2\;;\ 3}$

 

Si $-1\leq x<1$;

 

$$\begin{eqnarray} F(x) &=& p(X=-1)\nonumber\\ &=& \dfrac{1}{9}\Longrightarrow p(X=-1)\nonumber\\ &=& \dfrac{1}{9}.\nonumber \end{eqnarray}$$

 

Si $0\leq x<1$;

 

$$\begin{eqnarray} F(x) &=& p(X=-1)+p(X=0)\nonumber\\ &=& \dfrac{3}{9}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} &\Longrightarrow &\dfrac{1}{9}+p(X=0)=\dfrac{3}{9}\nonumber\\&\Longrightarrow &p(X=0)=\dfrac{3}{9}-\dfrac{1}{9}\nonumber\\&\Longrightarrow &p(X=0)=\dfrac{2}{9}\nonumber \end{eqnarray}$$

 

Si $1\leq x<2$;

 

$$\begin{eqnarray} F(x) &=& p(X=-1)+p(X=0)+p(X=1)\nonumber\\ &=& \dfrac{6}{9}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} &\Longrightarrow &\dfrac{3}{9}+p(X=1)=\dfrac{6}{9}\nonumber\\&\Longrightarrow &p(X=1)=\dfrac{6}{9}-\dfrac{3}{9}\nonumber\\&\Longrightarrow &p(X=1)=\dfrac{3}{9}\nonumber \end{eqnarray}$$

 

Si $2\leq x<3$;

 

$$\begin{eqnarray} F(x) &=& p(X=-1)+p(X=0)+p(X=1)+p(X=2)\nonumber\\ &=& \dfrac{8}{9}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} &\Longrightarrow &\dfrac{6}{9}+p(x=2)=\dfrac{8}{9}\nonumber\\&\Longrightarrow &p(x=2)=\dfrac{8}{9}-\dfrac{6}{9}\nonumber\\&\Longrightarrow &p(x=2)=\dfrac{2}{9}\nonumber \end{eqnarray}$$

 

Si $x\geq 3$;

 

$$\begin{eqnarray} F(x) &=& p(X=-1)+p(X=0)+p(X=1)+p(X=2)+p(X=3)\nonumber\\ &=& 1.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} &\Longrightarrow &\dfrac{8}{9}+p(X=3=1)\nonumber\\&\Longrightarrow &p(x=3)=1-\dfrac{8}{9}\nonumber\\&\Longrightarrow &p(X=3)=\dfrac{1}{9}.\nonumber \end{eqnarray}$$

 

$$\begin{array}{|c|c|c|c|c|c|} \hline x&-1&0&1&2&3\\ \hline p(X=x)&\dfrac{1}{9}&\dfrac{2}{9}&\dfrac{3}{9}&\dfrac{2}{9}&\dfrac{1}{9}\\ \hline \end{array}$$

 

c) $$\begin{eqnarray} p(X\leq 0) &=& p(X=-1)+p(X=0)\nonumber\\ &=& \dfrac{1}{9}+\dfrac{2}{9}\nonumber\\ &=& \dfrac{3}{9}\nonumber\\ &=& \dfrac{1}{3}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} p(X\geq 1) &=& p(X=1)+p(X=2)+p(X=3)\nonumber\\ &=& \dfrac{3}{9}+\dfrac{2}{9}\nonumber\\ &=& \dfrac{6}{9}\nonumber\\ &=& \dfrac{2}{3}.\nonumber \end{eqnarray}$$

 

d) $$\begin{eqnarray} E(X) &=& -1 p(X=-1)+0 p(X=0)+1 p(X=1)+2 p(X=2)+3 p(X=3)\nonumber\\ E(X)&=&-\left(1\times\dfrac{1}{9}\right)+\left(0\times\dfrac{2}{9}\right)+\left(1\times\dfrac{3}{9}\right)+\left(3\times\dfrac{1}{9}\right)\nonumber\\ &=& -\dfrac{1}{9}+\dfrac{3}{9}+\dfrac{4}{9}+\dfrac{3}{9}\nonumber\\ E(X) & = & 1.\nonumber \end{eqnarray}$$

 

e) $\sigma(X)=\sqrt{v(X)}$;

 

$$\begin{eqnarray} v(X) & = & E(X^{2})-(E(X))^{2}\nonumber\\ v(X) & = & \left[(-1)^{2}p(X=-1)+0^{2}p(X=0)+1^{2}p(X=1)+2^{2}p(X=2)+3^{2}p(X=3)\right]-1\nonumber\\ & = & \left[\left(1\times\dfrac{1}{9}\right)+\left(0\times\dfrac{2}{9}\right)+\left(1\times\dfrac{3}{9}\right)+\left(4\times\dfrac{2}{9}\right)+\left(9\times\dfrac{1}{9}\right)\right]-1\nonumber\\ & = & \dfrac{1}{9}+\dfrac{3}{9}+\dfrac{8}{9}+\dfrac{9}{9}-1\nonumber\\ v(X) & = & \dfrac{21}{9}-1\nonumber\\ \sigma(X) & = & \sqrt{\dfrac{12}{9}}\nonumber\\ & = & \dfrac{\sqrt{12}}{3}\nonumber\\ & = & \dfrac{2\sqrt{3}}{3}.\nonumber \end{eqnarray}$$

 

2) a) $$\begin{array}{|c|c|c|c|} \hline U_{1}\backslash U_{2}&-2&-1&0\\ \hline 1&-1&0&1\\ \hline 2&0&1&2\\ \hline 3&1&2&3\\ \hline \end{array}$$

 

b) Soit $V$ l'ensemble des valeurs possibles de $Y.$

 

$V={-1\;,\ 0\;,\ 1\;,\ 2\;,\ 3}$

 

$p(Y=-1)=\dfrac{1}{9}\;;\ p(Y=0)=\dfrac{2}{9}$

 

$p(Y=1)=\dfrac{3}{9}\;;\ p(Y=2)=\dfrac{2}{9}$

 

$p(Y=3)=\dfrac{1}{9}.$

 

$$\begin{array}{|c|c|c|c|c|c|} \hline x&-1&0&1&2&3\\ \hline p(Y=x)&\dfrac{1}{9}&\dfrac{2}{9}&\dfrac{3}{9}&\dfrac{2}{9}&\dfrac{1}{9}\\ \hline \end{array}$$

 

$Y\text{ et }X$ ont la même loi de probabilité.

1) $$\begin{eqnarray} \left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\right)^{2} & = & \left(\dfrac{\sqrt{2}}{2}\right)^{2}+2\left(\dfrac{\sqrt{2}}{2}\right) \left(\dfrac{\sqrt{2}}{2}\mathrm{i}\right)+\left(\dfrac{\sqrt{2}}{2}\mathrm{i}\right)^{2}\nonumber\\ & = & \dfrac{2}{4}+\mathrm{i}-\dfrac{2}{4}\nonumber\\ & = & \mathrm{i}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} z^{2}-\mathrm{i}=0 & \Longleftrightarrow & z^{2}=\mathrm{i}\nonumber\\ & \Longleftrightarrow & z^{2}=\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\right)^{2}\nonumber\\ & \Longleftrightarrow & z=\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\text{ ou }z=-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber \end{eqnarray}$$

 

$S=\left\lbrace\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\;;\ -\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\right\rbrace$

 

2) a) $\alpha$ est une solution de l'équation 

 

$$\begin{eqnarray} p(z)=0& \Longleftrightarrow & p(\alpha)=0\nonumber\\& \Longleftrightarrow & \alpha^{3}+\alpha^{2}-\mathrm{i}\alpha-\mathrm{i}=0\nonumber\\& \Longleftrightarrow & \alpha^{3}+\alpha^{2}+\mathrm{i}(-\alpha-1)=0\nonumber\\ \alpha^{3}+\alpha^{2}+0\qquad (1)\nonumber\\ -\alpha-1=0\qquad (2)\nonumber\\ & \Longleftrightarrow & \alpha=-1\;;\ (-1)^{3}+(-1)^{2}=-1+1=0.\quad(2)\nonumber \end{eqnarray}$$

 

donc $\alpha=-1$

 

b) Comme -1 est une racine de $p$, donc il existe un polynôme $g$ tel que $p(z)=(z+1)g(z).$

 

$$\begin{array}{|c|c|c|c|c|} \hline &1&1&-\mathrm{i}&-\mathrm{i}\\ \hline -1& &-1&0&\mathrm{i}\\ \hline  &1&0&-\mathrm{i}&0\\ \hline \end{array}$$

 

$g(z)=z^{2}-\mathrm{i}$

 

Les solutions de l'équation $p(z)=0$ sont : -1 et les racines de $g.$

 

$$\begin{eqnarray} g(z)=0& \Longleftrightarrow & z^{2}-\mathrm{i}=0\nonumber\\ & \Longleftrightarrow & z=\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\text{ ou }z=-\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber \end{eqnarray}$$

 

$S=\left\lbrace-1\;;\ \dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\;;\ -\dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\right\rbrace$

 

3) a) $$\begin{eqnarray} z_{A} & = & \dfrac{\sqrt{2}}{2}(1+\mathrm{i})\nonumber\\ & = & \dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber\\ & = & \cos\dfrac{\pi}{4}+\mathrm{i}\sin\dfrac{\pi}{4}\nonumber\\ & = & \mathrm{e}^{\mathrm{i}\dfrac{\pi}{4}}.\nonumber  \end{eqnarray}$$

 

$$\begin{eqnarray} z_{B} & = & -\dfrac{\sqrt{2}}{2}(1+\mathrm{i})\nonumber\\ & = & -\dfrac{\sqrt{2}}{2}-\mathrm{i}\dfrac{\sqrt{2}}{2}\nonumber\\ & = & \cos\dfrac{5\pi}{4}+\mathrm{i}\sin\dfrac{5\pi}{4}\nonumber\\ & = & \mathrm{e}^{\mathrm{i}\dfrac{5\pi}{4}}.\nonumber  \end{eqnarray}$$

 

b)

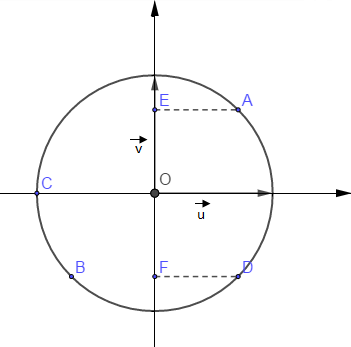
4) a) $$\begin{eqnarray} z_{D} & = & \overline{z}_{A}\nonumber\\ & = & \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber \end{eqnarray}$$

 

b) $$\begin{eqnarray} z_{D}-z_{C} & = & \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}+1\nonumber\\ & = & \dfrac{\sqrt{2}}{2}+1-\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber\\ & = & \dfrac{\sqrt{2}+2}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} z_{A}-z_{C} & = & \dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}+1\nonumber\\ & = & \dfrac{\sqrt{2}}{2}+1+\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber\\ & = & \dfrac{\sqrt{2}+2}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} \dfrac{z_{D}-z_{C}}{z_{A}-z_{C}} & = & \dfrac{\dfrac{\sqrt{2}+2}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}}{\dfrac{\sqrt{2}+2}{2}+\dfrac{\sqrt{2}}{2}\mathrm{i}}\nonumber\\ & = & \dfrac{\sqrt{2}+2-\mathrm{i}\sqrt{2}}{\sqrt{2}+2+\mathrm{i}\sqrt{2}}\nonumber\\ & = & \dfrac{(\sqrt{2}+2-\mathrm{i}\sqrt{2})^{2}}{(\sqrt{2}+2+\mathrm{i}\mathrm{2})(\sqrt{2}+2-\mathrm{i}\sqrt{2})}\nonumber\\ & = & \dfrac{\left[\left(\sqrt{2}+2\right)-\mathrm{i}\sqrt{2}\right]^{2}}{\left(\sqrt{2}+2\right)^{2}+(\sqrt{2})^{2}}\nonumber\\ & = & \dfrac{(\sqrt{2}+2)^{2}-2(\sqrt{2}+2)\mathrm{i}\sqrt{2}-2}{2+4\sqrt{2}+4+2}\nonumber\\ & = & \dfrac{2+4\sqrt{2}+4-4\mathrm{i}-4\mathrm{i}\sqrt{2}-2}{8+4\sqrt{2}}\nonumber\\ & = & \dfrac{4+4\sqrt{2}-(4+4\sqrt{2})\mathrm{i}}{8+4\sqrt{2}}\nonumber\\ & = & \dfrac{1+\sqrt{2}-(1+\sqrt{2})\mathrm{i}}{2+\sqrt{2}}\nonumber\\ & = & \dfrac{\sqrt{2}}{2}(1-\mathrm{i})\nonumber\\ & = & \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2}\mathrm{i}\nonumber\\ & = & \cos\left(-\dfrac{\pi}{4}\right)+\mathrm{i}\sin\left(-\dfrac{\pi}{4}\right)\nonumber\\\dfrac{z_{D}-z_{C}}{z_{A}-z_{C}} & = & \mathrm{e}^{-\mathrm{i}\dfrac{\pi}{4}}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} \left|\dfrac{z_{D}-z_{C}}{z_{A}-z_{C}}\right|=\left|\mathrm{e}^{-\mathrm{i}\dfrac{\pi}{4}}\right| & \Longrightarrow & \dfrac{|z_{D}-z_{C}|}{|z_{A}-z_{C}|}=1\nonumber\\& \Longrightarrow & \dfrac{CD}{CA}=1\nonumber\\ & \Longrightarrow & CD=CA\nonumber \end{eqnarray}$$

 

$\Longrightarrow\ ABC$ est isocèle de sommet principal $C.$

 

5) a) Soit $\mathcal{P}$ le plan

 

$$\begin{eqnarray} S\ :\ \mathcal{P} & \rightarrow & \mathcal{P}\nonumber\\ M(z) & \mapsto & M'(z')\nonumber\\ z' & = & az+b\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} S(E)=A& \Longleftrightarrow & z_{A}=a z_{E}+b\nonumber\\ & \Longleftrightarrow & \dfrac{\sqrt{2}}{2}(1+\mathrm{i})=a\times\dfrac{\sqrt{2}}{2}\mathrm{i}+b\nonumber\\& \Longleftrightarrow & \sqrt{2}(1+\mathrm{i})=a\sqrt{2}\mathrm{i}+2 b\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} S(F)=B& \Longleftrightarrow & z_{B}=a z_{F}+b\nonumber \end{eqnarray}$$

 

$F$ est le symétrique de $E$ par rapport

 

$$\begin{eqnarray} O& \Longleftrightarrow & \overrightarrow{EO}=\overrightarrow{OF}\nonumber\\& \Longleftrightarrow & z_{O}-z_{E}=z_{F}-z_{O}\nonumber\\ & \Longleftrightarrow & -z_{E}=z_{F}\nonumber\\& \Longleftrightarrow & z_{F}=-\dfrac{\sqrt{2}}{2}\mathrm{i}.\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} z_{B}=az_{F}+b & \Longleftrightarrow & -\dfrac{2}{2}(1+\mathrm{i})=-a\times\dfrac{\sqrt{2}}{2}\mathrm{i}+b\nonumber\\& \Longleftrightarrow & -\sqrt{2}(1+\mathrm{i})=-a\sqrt{2}\mathrm{i}+2b.\nonumber \end{eqnarray}$$

 

$$\left\lbrace\begin{array}{llll} \sqrt{2}(1+\mathrm{i})&=&a\sqrt{2}\mathrm{i}+2b&(1)\\ -\sqrt{2}(1+\mathrm{i})&=&-a\sqrt{2}\mathrm{i}+2b&(2) \end{array}\right.$$ $$\overline{0=4b\\b=0}$$

 

$$\begin{eqnarray} (1)&\Longleftrightarrow & \sqrt{2}(1+\mathrm{i})=a\sqrt{2}\mathrm{i}\nonumber\\& \Longleftrightarrow & 1+\mathrm{i}=a\mathrm{i}\nonumber\\ & \Longleftrightarrow & a=\dfrac{1+\mathrm{i}}{\mathrm{i}}\nonumber\\&\Longleftrightarrow & a=\dfrac{1}{\mathrm{i}}+1\nonumber\\ & \Longleftrightarrow & a=1-\mathrm{i}\nonumber \end{eqnarray}$$

 

$a=1-\mathrm{i}\text{ et }b=0.$

 

D'où $z'=(1-\mathrm{i})z.$

 

$1-\mathrm{i}\neq 1$, donc $S$ est la similitude de centre $\Omega$ de rapport $k$ et d'angle $\theta.$

 

$z_{\Omega}=\dfrac{b}{1-a}=\dfrac{0}{1-a}=0=z_{0}\Longrightarrow \Omega=0.$

 

$$\begin{eqnarray} k &=& |a|=|1-\mathrm{i}|\nonumber\\ &=& \sqrt{1^{2}+(-1)^{2}}\nonumber\\ &=& \sqrt{1+1}\nonumber\\ &=& \sqrt{2}\nonumber \end{eqnarray}$$

 

$^\theta=arg(a)\equiv-\dfrac{\pi}{4}[2\pi]\;;\ \theta\equiv-\dfrac{\pi}{4}2\pi].$

 

$S$ est la similitude de centre $O$, de rapport $\sqrt{2}$ et d'angle $-\dfrac{\pi}{4}.$

 

b) $(\mathcal{C'})$ est le cercle de centre $S(E)$ et de rayon $1\times\sqrt{2}.$

 

$S(E)=A\;;\ 1\times\sqrt{2}=\sqrt{2}.$

 

$(\mathcal{C'})$ est le cercle de centre $A\text{ et de rayon }\sqrt{2}.$

Partie A

 

1) L'équation caractéristique de $E$ est : $r^{2}+4r+4=0.$

 

$$\begin{eqnarray} r^{2}+4 r+4=0 &\Longleftrightarrow &(r+2)^{2}=0\nonumber\\ &\Longleftrightarrow & r+2=0\nonumber\\ &\Longleftrightarrow & r=-2.\nonumber \end{eqnarray}$$

 

$h(x)=(\lambda x+\mu)\mathrm{e}^{-2x}\text{ ou }(\lambda\;,\ \mu)\in\mathbb{R}^{2}.$

 

2) a) $\varphi(x)=ax+b\;;\ \varphi'(x)=a\;;\ \varphi''(x)=0.$

 

$$\begin{eqnarray} \varphi\text{ est solution de }(F)&\Longleftrightarrow &\varphi''(x)+4\varphi'(x)+4\varphi(x)=-4x\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & 4 a+4 a x+4 b=-4 x\;,\ \forall\;x\in\mathbb{R}\nonumber\\ &\Longleftrightarrow&\left\lbrace\begin{array}{lcl} 4a&=&-4\\ 4a+4b&=&0 \end{array}\right.\nonumber\\ &\Longleftrightarrow&\left\lbrace\begin{array}{lcl} a&=&-1\\ a+b&=&0 \end{array}\right.\nonumber\\&\Longleftrightarrow&\left\lbrace\begin{array}{lcl} a&=&-1\\ -1+b&=&0 \end{array}\right. \nonumber\\  &\Longleftrightarrow&\left\lbrace\begin{array}{lcl} a&=&-1\\ b&=&1 \end{array}\right.\end{eqnarray}$$

 

b) $$\begin{eqnarray} f\text{ est solution de }(F)&\Longleftrightarrow & f''(x)+4 f'(x)+4 f(x)=-4x\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & f''(x)+4 f'(x)+4 f(x)=\varphi''(x)+4\varphi'(x)+4\varphi(x)\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow &f''(x)-\varphi''(x)+4 f'(x)-4\varphi'(x)+4f(x)-4\varphi(x)=0\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & (f-\varphi)''(x)+4(f-\varphi)'(x)+4(f-\varphi)(x)=0\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & f-\varphi\text{ est solution de }(E).\nonumber \end{eqnarray}$$

 

c) $$\begin{eqnarray} f\text{ est solution de }(F)&\Longleftrightarrow & f-\varphi\text{ est solution de }(E)\nonumber\\&\Longleftrightarrow & (f-\varphi)=(\lambda x+\mu)\mathrm{e}^{-2 x}\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & f(x)-\varphi(x)=(\lambda x+\mu)\mathrm{e}^{-2 x}\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & f(x)=(\lambda x+\mu)\mathrm{e}^{-2 x}+\varphi(x)\;,\ \forall\;x\in\mathbb{R}\nonumber\\&\Longleftrightarrow & f(x)=(\lambda x+\mu)\mathrm{e}^{-2 x}-x+1\;,\ \forall\;x\in\mathbb{R}\nonumber  \end{eqnarray}$$

 

Les solutions de $(F)$ sont les fonctions définies sur $\mathbb{R}$ et de la forme $x\mapsto (\lambda x+\mu)\mathrm{e}^{-2x}-x+1\;,\text{ où }(\lambda\;,\ \mu)\text{ d'écrit }\mathbb{R}^{2}.$

 

d) $f(x)=(\lambda x+\mu)\mathrm{e}^{-2x}-x+1$

 

$$\begin{eqnarray} f(0)=2&\Longleftrightarrow & (\lambda{0}+\mu)\mathrm{e}^{-2(0)}-0+1=2\nonumber\\&\Longleftrightarrow & \mu+1=2\nonumber\\&\Longleftrightarrow & \mu=1\nonumber \end{eqnarray}$$

 

$f'(x)=\lambda\mathrm{e}^{-2x}-2(\lambda x+\mu)\mathrm{e}^{-2x}-1$

 

$$\begin{eqnarray} f'(0)=-2&\Longleftrightarrow & \lambda-2\mu-1=-2\nonumber\\&\Longleftrightarrow & \lambda-2(1)-1=-2\nonumber\\&\Longleftrightarrow & \lambda-3=-2\nonumber\\&\Longleftrightarrow &\lambda=1.\nonumber \end{eqnarray}$$

 

$\lambda=1\text{ et }\mu=1\;;\text{ d'où }f(x)=(x+1)\mathrm{e}^{-2x}-x+1.$

 

Partie B

 

1) a) Soit $x\in\;[0\;,\ +\infty[.$

 

$$\begin{eqnarray} f'(x)& = & \mathrm{e}^{-2 x}-2 x\mathrm{e}^{-2 x}-2\mathrm{e}^{-2 x}-1\nonumber\\ &=& -\mathrm{e}^{-2 x}-2 x\mathrm{e}^{-2 x}-1\nonumber\\ f'(x) &=& 2\mathrm{e}^{-2 x}-2\left[\mathrm{e}^{-2 x}-2 x\mathrm{e}^{-2 x}\right]\nonumber\\ &=& 2\mathrm{e}^{-2 x}-2\mathrm{e}^{-2 x}+4 x\mathrm{e}^{-2 x}\nonumber\\ &=& 4 x\mathrm{e}^{-2 x}.\nonumber \end{eqnarray}$$

 

b) $\forall\;x\in\;[0\;,\ +\infty[\;,\ f'(x)=4\mathrm{e}^{-2x}$

 

$\forall\;x\in\;[0\;,\ +\infty[\;,\mathrm{e}^{-2x}>0$, donc $f''(x)$ est du signe de $x$, donc $f''(x)\geq 0.$

 

$f'(0)=-2$ ;

 

$f'(x)=-\mathrm{e}^{-2x}-\dfrac{2x}{\mathrm{e}2x}-1\;;\ \lim_{x\rightarrow +\infty}-2x=-\infty$

 

$\lim_{x\rightarrow +\infty}\mathrm{e}^{-2x}=0\;;\ \lim_{x\rightarrow +\infty}\dfrac{2x}{\mathrm{e}^{2x}}=0$

 

$\lim_{x\rightarrow +\infty}f'(x)=-1$

 

$$\begin{array}{|c|lccr|} \hline x&0& & &+\infty\\ \hline f''(x)&0&+& &\\ \hline & & & &-1\\ f'& & &\nearrow &\\ &-2& & &\\ \hline \end{array}$$

 

c) $\forall\;x\in\;[0\;,\ +\infty[\;,\ f'(x)\in\;[-2\;,\ -1[\Longrightarrow f'(x)<0$

 

2) $$\begin{eqnarray} \lim_{x\rightarrow -\infty}\dfrac{x+1}{x} &=& \lim_{x\rightarrow -\infty}\dfrac{x}{x}\nonumber\\ &=& \lim_{x\rightarrow -\infty}1\nonumber\\ &=&1;\nonumber \end{eqnarray}$$

 

$\lim_{x\rightarrow -\infty}f(x)=\ln 1=0$

 

$$\begin{eqnarray} \lim_{x\rightarrow -1^{-}}\dfrac{x+1}{x}=0^{+} &\Longrightarrow &\lim_{x\rightarrow -1^{-}}\ln\left(\dfrac{x+1}{x}\right)=-\infty\nonumber\\&\Longrightarrow &\lim_{x\rightarrow -1^{-}}f(x)=-\infty\nonumber \end{eqnarray}$$

 

$$\begin{eqnarray} \forall\;x<-1\;,\ f'(x) &=& \dfrac{\dfrac{x-x-1}{x^{2}}}{\dfrac{x+1}{x}}\nonumber\\ &=& \dfrac{(x-x-1)x}{x^{2}(x+1)}\nonumber\\ &=& \dfrac{x-x-1}{x(x+1)}\nonumber\\ &=& \dfrac{-1}{x(x+1)}.\nonumber \end{eqnarray}$$

 

$\forall\;x<-1\;,\ x(x+1)>0\Longrightarrow f'(x)<0.$

 

$$\begin{array}{|c|lcr|} \hline x&-\infty& &-1\\ \hline f'(x)& &-& \\ \hline &0& &\\ f& &\searrow &\\ & & &-\infty\\ \hline \end{array}$$

 

3) $f(0)=2\;;\ \forall\;x\in\;[0\;,\ +\infty[\;,\ f(x)=x\left(\mathrm{e}^{-2x}+\dfrac{\mathrm{e}^{-2x}}{x}-1+\dfrac{1}{x}\right)$

 

$\lim_{x\rightarrow +\infty}x=+\infty\;;\ \lim_{x\rightarrow +\infty}\mathrm{e}^{-2x}=0$;

 

$\lim_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{-2x}}{x}=0\;;\ \lim_{x\rightarrow +\infty}\dfrac{1}{x}=0$

 

$\lim_{x\rightarrow +\infty}\mathrm{e}^{-2x}+\dfrac{\mathrm{e}^{-2x}}{x}-1+\dfrac{1}{x}=-1\;;\ \lim_{x\rightarrow +\infty}f(x)=-\infty$

 

4) $f(]-\infty\;,\ -1[)=]-\infty\;,\ 0[\;,\text{ donc }\forall\;x\in\;]-\infty\;,\ -1[\;,\ f(x)<0\Longrightarrow f(x)\neq 0.$

 

$f$ est continue et strictement décroissante sur $[0\;,\ +\infty[$, donc $f$ est une bijection de $[0\;,\ +\infty[$ sur $f([0\;,\ +\infty[)=]-\infty\;,\ 2].$ 

 

Or $0\in\;]-\infty\;,\ 2]$, donc il existe un unique $\alpha\in\;[0\;,\ +\infty[$ tel que $f(\alpha)=0.$

 

En conséquence l'équation $f(x)=0$ admet une unique solution $\alpha.$

 

$f(1)=\mathrm{e}^{-2}+\mathrm{e}^{-2}-1+1=2\mathrm{e}^{-2}$;

 

$f(2)=2\mathrm{e}^{-4}+\mathrm{e}^{-4}-2+1=3\mathrm{e}^{-4}-1.$

 

$f(1)>0\;,\ f(2)<0\;;\ f(1)f(2)<0$

 

$\Longrightarrow 1<\alpha<2\Longrightarrow 1\leq\alpha\leq 2.$

 

5) $\forall\;x\geq 0\;,\ f(x)=x\mathrm{e}^{-2x}+\mathrm{e}^{-2x}-x+1.$

 

Or $\lim_{x\rightarrow +\infty}x\mathrm{e}^{-2x}+\mathrm{e}^{-2x}=0$, donc la droite $(\mathcal{D})$ d'équation $y=-x+1$ est asymptote oblique à $(\mathcal{C}_{f})\text{ en }+\infty.$

 

$f(x)-(-x+1)=x\mathrm{e}^{-2x}+\mathrm{e}^{-2x}=\mathrm{e}^{-2x}(x+1)$ 

 

$\forall\;x\geq 0\;,\ \mathrm{e}^{-2x}>0\text{ et }x+1>0$, donc

 

$\forall\;x\in\;[0\;,\ +\infty[\;,\ f(x)-(x+1)>0$

 

$\Longrightarrow (\mathcal{C}_{f})$ est au-dessus de $(\mathcal{D}).$

 

6) $\lim_{x\rightarrow -\infty}f(x)=0$ donc la droite d'équation $x=-1$ est asymptote horizontale à $(\mathcal{C}_{f})\text{ en }-\infty.$

 

$\lim_{x\rightarrow -\infty}f(x)=-\infty$, donc la droite d'équation $x=-1$ est asymptote verticale à $(\mathcal{C}_{f}).$

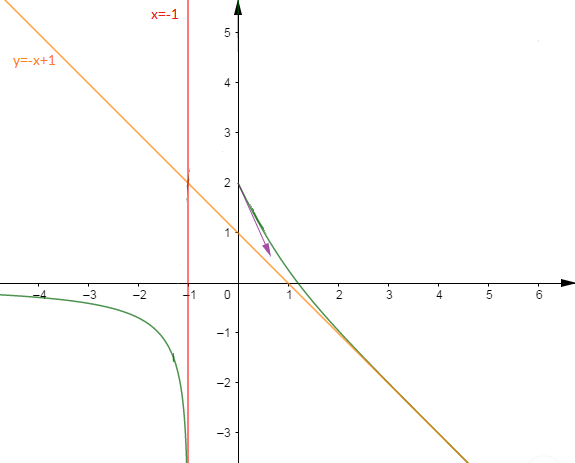
$f'(0)=-2\;;\ f(1)=\mathrm{e}^{-2}+\mathrm{e}^{-2}=2\mathrm{e}^{-2}\simeq 0.27$

 

$f(-2)=-\ln 2\simeq -0.69$

 

$f(-1.5)=-\ln 3\simeq -1.1\;;\ f(-3)=\ln\dfrac{2}{3}\simeq -0.41.$